Примечания. 1. Объяснение математики нелокальности электрона до наблюдения дается в следующей сноске

1. Объяснение математики нелокальности электрона до наблюдения дается в следующей сноске.

2. Общее уравнение, или паттерн, для частицы описывает тенденцию ее обнаружения в положении x в определенное время t. Если мы называем эту тенденцию волновой функцией, тогда ψ зависит от x и t (является функцией x и t).

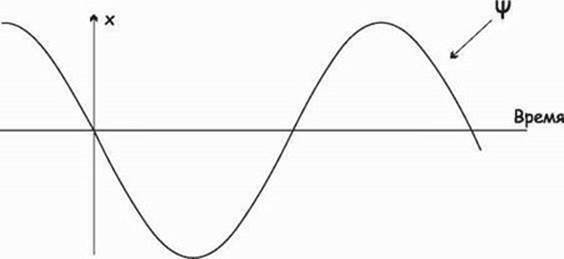
Рис. 14.5. Волновой паттерн. Надпись на горизонтальной оси – Время

Поскольку зависимость иногда носит волноподобный характер, мы можем использовать общее волновое уравнение. В наиболее общей форме оно выглядит так:

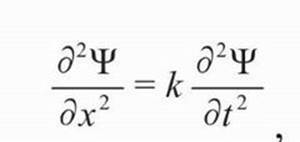
что попросту означает, что ψ – тенденция быть в точке x на экране в момент t – зависит от x и t периодическим образом. (Спасибо Лейбницу и Ньютону за создание дифференциального исчисления!)

В квантовой механике волновое уравнение называется дифференциальным уравнением в частных производных и может быть записано для одной частицы в одном измерении как

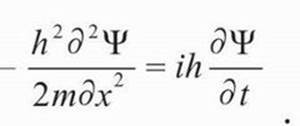
Волновое уравнение для одной частицы при отсутствии внешних сил

Одно из решений волнового уравнения можно записать как

ψ = Ae i(ωt-κx)

или как любое сложение или суперпозицию этих ψ. Отметьте присутствие в приведенной выше формуле мнимого числа i. Поэтому ψ представляет собой комплексное число. Читатель вспомнит это решение из главы 8 о комплексных числах, которые можно использовать для представления гармоник и музыки. (Математика комплексных чисел лучше всего подходит для систем с колебаниями вследствие обеспечиваемой ею легкости вычисления и выражения подобных движений.) См. примечания 2 и 3 к главе 8.

В любом случае, волновая функция ψ имеет волноподобное решение, которое в общем виде можно выразить экспоненциальной формой

ψ = Ae i(ωt-κx)

Экспоненциалы делают дифференциальные уравнения очень простыми. При их подстановке сложное на вид уравнение становится алгебраическим, поскольку дифференциал экспоненциальной функции превращает показатель степени числа e в простой множитель.

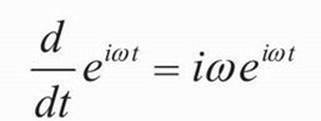
Вторая производная делает то же самое, превращая в множитель еще одно iω. Таким образом, дифференцирование экспоненциалов оказывается умножением.

В случае квантовой механики w представляет собой частоту, связанную с классическим выражением для энергии E = hω, где h – постоянная Планка, и h = 2Πк. Волновое число к описывает импульс или момент количества движения электрона p = hk. Если бы мы знали точное волновое число, то знали бы импульс квантового объекта.

Замечательный аспект волнового уравнения, иногда называемый амплитудой, состоит в том, что абсолютный квадрат ψ, который можно получить посредством конъюгации, дает вероятность нахождения частицы в точке x в момент времени t.

Отметьте, что из волновой функции для электрона при отсутствии внешних сил следует равная вероятность его нахождения в любом месте Вселенной! Это означает, что до измерения нам точно не известно, где находится частица. Однако абсолютное значение избавляется от мнимых факторов. Поэтому вероятность ƒ для частицы не меняется в зависимости от пространства или времени. Частица обладает определенной энергией. Вот почему мы иногда говорим, что атом на определенном энергетическом уровне находится в стационарном состоянии.

Квантовая волновая функция и квантовая механика более подробно описаны в Приложении.

3. Математическое выражение результатов конъюгации представляет собой абсолютное действительное значение комплексного числа. Физика интерпретирует это число как представляющее вероятность нахождения частицы в определенной точке на экране.

4. Об этом говорится в главе 8

Date: 2015-08-15; view: 359; Нарушение авторских прав