Примечания. 1. Чтобы это проверить, вообразите, что вы кладете на пол линейку между своими ногами и зеркалом

1. Чтобы это проверить, вообразите, что вы кладете на пол линейку между своими ногами и зеркалом. Если вы стоите в комнате в точке a + bi и смотрите прямо вниз, туда, где кончаются ваши ступни, то сперва увидите деление линейки «100 см». Перемещая взгляд по линейке в направлении зеркала, вы будете видеть деления «95», «94», «93» и так далее, пока не дойдете до деления «1 см» и, наконец, до стены.

Затем, если зеркало такое хорошее, что вы едва его замечаете, вы увидите в зеркале еще одну линейку. Эта линейка представляет собой отражение той, что лежит у ваших ног, и счет ее делений идет в обратном направлении.

Прослеживая взглядом эту линейку, вы отсчитываете 1 см, потом 2, 3, 4 и так далее и, наконец, 100 см. Тогда, посмотрев вверх, вы увидите в зеркале самого себя, смотрящего вам в глаза! Ваше зеркальное отражение выглядит в точности как вы – с той лишь разницей, что вы находитесь на +100 см, а ваш двойник на -100 см.

Между вами и вашим двойником есть и другие различия. Однако пока давайте думать только о том, что вы находитесь на +100 см, а ваш двойник на -100 см.

2. В примечаниях 2, 3 и 4 обсуждаются более удивительные характеристики комплексных чисел. Вы можете выражать геометрию комплексных чисел тригонометрически, то есть в терминах углов.

Примем, что 9 – это угол между R и осью х, как показано ниже на рис. 8.4 (tan означает тангенс, cos означает косинус; tan(θ) означает тангенс угла 9).

Рис. 8.4 Комплексное число, выраженное в терминах углов Более подробно о комплексных числах можно прочитать в книгах Руэла В. Чарчхилла «Комплексные переменные и приложения» (Ruel V. Churchill. Complex Variables and Applications) и Ханса Швердтфегера «Геометрия комплексных чисел» (Hans Schwerdtfeger. Geometry of Complex Numbers).

Математики называют [cos(θ) + isin(θ)] угловым множителем комплексного числа и в соответствии с законами алгебры и тригонометрии обозначают его как еiθ. Число е может использоваться для сокращения длинных тригонометрических выражений, что делает вычисления простыми. Это отчасти связано с той особенностью показательных функций, что для двух углов θ, и θ2 мы имеем

отсюда z = R [cos(θ) + i sin(θ)] = Re iθ.

3. Приведенное выше уравнение z = K[cos(θ) + isin(θ)] = К ei θ означает, ни много ни мало, что z имеет периодическое поведение, поскольку при возрастании угла 9 cos(θ) и isin(θ) претерпевают периодические волнообразные изменения. Иными словами, имеются две волны – одна действительная, а другая мнимая, или не совпадающая по фазе с действительной на 900. См. рис. 8.5

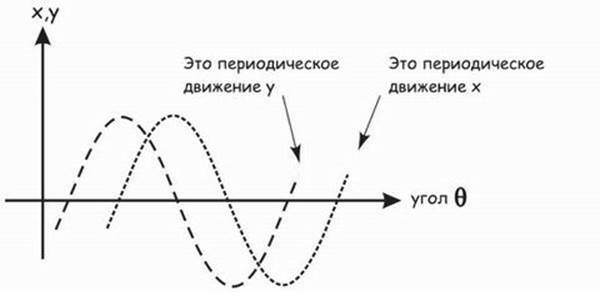
Рис. 8.5. Периодическое движение x и у

С показательными функциями (экспонентами) иметь дело легче, чем с синусами и косинусами. Поэтому в физике для представления колебаний постоянно используются комплексные числа в форме ei (θ1+ θ2) ei (θ1+ θ2). Для представления колебаний, которые можно измерять, например качания маятника, используется только действительная часть числа z. Мнимым элементом пренебрегают.Хорошее элементарное обсуждение математики и волн для ученых можно найти в фейнмановских «Лекциях по физике» (том I, гл. 23).Еще один интересный аспект действительных и мнимых чисел состоит в том, что действительный и мнимый аспекты z подобны двум разным измерениям реальности, двигающимся вместе, но не вполне вместе. Вообще, если действительная и мнимая оси вращаются, мы можем видеть, что ось мнимого числа Y всегда отстает от действительной оси X на угол 90°, как показано на рис. 8.6.

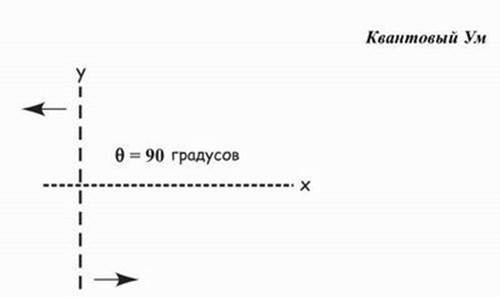
Рис. 8.6. Вращение комплексной плоскости на 90 градусов

По аналогии можно сказать, что воображаемый мир всегда находится в другом измерении по отношению к реальному или, наоборот, что при возрастании 9 оси X и Y выглядят как две волны – одна впереди, а другая чуть позади, – как если бы они были барабанами, звук которых отдается эхом «бум бум», пауза, «бум бум», пауза, «бум бум» и так далее. Две волны, не совпадающие по фазе друг с другом, графически показаны на рисунке выше. Это аналогично ритму музыки на заднем плане нашего переживания.

В одной из последующих глав я покажу, что в квантовой физике периодическое поведение комплексных чисел (волновое уравнение) используется для описания невидимого состояния материальной системы. Состояние физической системы, например маленького шарика, элементарной частицы или человека, в каждой точке пространства и времени может быть представлено комплексным числом.

4. Если мы проводим линию R из центра к точке a + ib, то она выглядит как путь между этим комплексным числом и центром комплексной плоскости. См. рис. 8.7.

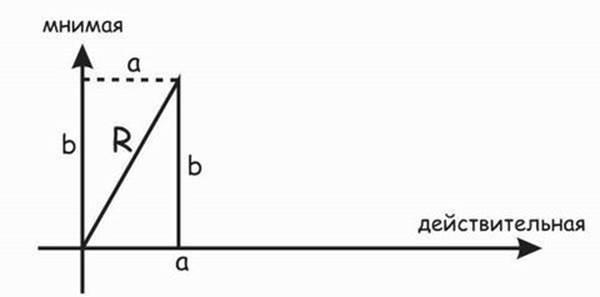
Рис. 8.7. Линия R на комплексной плоскости Какова длина R? R представляет собой длинную сторону треугольника с двумя другими сторонами а и b. R – это длинная сторона (гипотенуза), b – вертикальная сторона (катет) и a – горизонтальная сторона (катет).

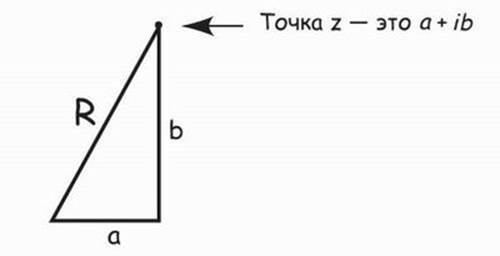
Рис. 8.8. R – это часть прямоугольного треугольника

Греческий ученый Евклид заимствовал информацию у вавилонян и открыл, как можно было бы измерить R, зная а и b. Оказывается, что если есть две стороны треугольника, которые перпендикулярны друг другу, формула Евклида говорит, что квадрат длинной стороны, R, равен сумме квадратов меньших сторон. То есть

R2 = а2 + b2

это формула Евклида для прямоугольных треугольников^[13].

Таким образом, умножение комплексного числа на его конъюгат дает нам R – расстояние точки от центра.

5. Помножим а + ib на а – ib. Получается

а2 – iab + iab – i2b2.

Если помнить, что i2 = -1 и заметить, что -mb и +rnb взаимно вычитаются, то остается

(а + ib) х (а – ib) = а2 + b2.

Математики называют выражение (а + ib^ifl – ib) абсолютным квадратом числа (а + ib). Например, если а = 3 и b = 4, то абсолютный квадрат комплексного числа 3 + 4i будет равен (3 + 4i)x(3 – 4i) = 32 + 42 или 9 + 16 или 25. Это действительное число без всякой примеси мнимых чисел.

6. С математической точки зрения, процесс конъюгации похож на возведение в квадрат, но чуть-чуть отличается от него. Возведение комплексных чисел в квадрат дает другие такие числа, в то время как конъюгация и получение абсолютного значения дает действительные числа!

Вот как это получается. Если возводим комплексное число типа а + ib в квадрат, то умножаем его само на себя и получаем комплексное число, то есть сочетание действительного и мнимого чисел, поскольку:

(а + ib) х (а + ib) = а2 + аА + аА – b2 = а2 + 2аА – b2.

Но для того чтобы получить абсолютное значение комплексного числа а + ib, мы конъюгируем его, или умножаем его на его конъюгат:

(а + ib) х (а – ib) = а2 – mb + mb + -i2b2,

но поскольку i2 = -1, мы получаем

(a + ib) х (a – ib) = a2 + b2,

как в примечании 5. Таким образом, получение абсолютного значения числа похоже на возведение числа в квадрат, за исключением того, что абсолютное значение не содержит никаких мнимых чисел. В отличие от конъюгации, возведение комплексного числа в квадрат дает

a2 + 2aib —Ь2,

в то время как абсолютное значение, получающееся в результате конъюгации, это a2 + b2 – действительное число, поскольку в нем нет никаких i.

Date: 2015-08-15; view: 478; Нарушение авторских прав