
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Расчет напряженности электрического поля трехфазной линии по методу зеркальных отображений
|
|
Рассмотрим одну фазу линии, например фазу А (рис. 2), приняв заряд провода положительным 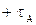 , а заряд его зеркального отображения отрицательным
, а заряд его зеркального отображения отрицательным 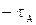 .
.
Модуль вектора напряженности электрического поля в некоторой точке P, обусловленного зарядом 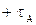 , В/м:
, В/м:
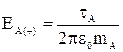 , (3.1)
, (3.1)
где 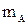 - кратчайшее расстояние от точки P до фазы A, м.
- кратчайшее расстояние от точки P до фазы A, м.
Модуль вектора напряженности электрического поля в некоторой точке P, обусловленного зарядом 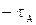 , В/м:
, В/м:
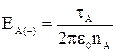 , (3.2)
, (3.2)
где 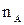 - кратчайшее расстояние от точки P до зеркального отображения фазы A, м.
- кратчайшее расстояние от точки P до зеркального отображения фазы A, м.
Разложим векторы 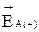 и
и 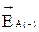 на их составляющие по горизонтали
на их составляющие по горизонтали 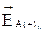 и
и 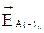 , и вертикали
, и вертикали 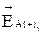 и
и 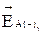 (рисунок 2).
(рисунок 2).
Модули этих векторов определяются по выражениям:
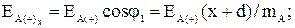 (3.3)
(3.3)
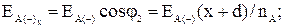 (3.4)
(3.4)
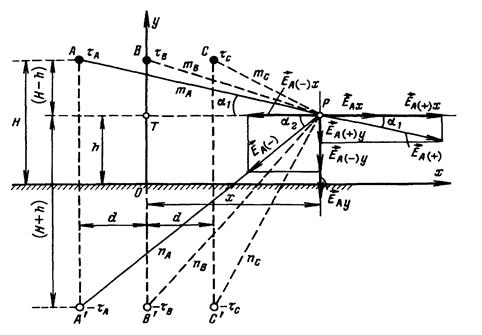
Рис. 2 – Расчет напряженности электрического поля трехпроводной воздушной линии электропередачи в точке P методом зеркальных отображений.
А, В, С – фазы (провода) линии; А/, В/, С/ – зеркальные отображения фаз;
mA, mB, mC – кратчайшие расстояния от точки Р до фаз линий; nA, nB, nC – кратчайшие расстояния от точки Р до зеркальных отображений фаз.
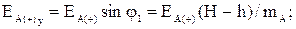 (3.5)
(3.5)
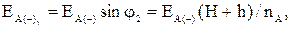 (3.6)
(3.6)
где x - расстояние по горизонтали от вертикальной оси симметрии линии до рассматриваемой точки P, м;
d – расстояние между осями соседних проводов линии, м;
H – высота размещения провода над землей, м;
h – высота точки P над землей, м.
Сложение векторов 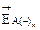 и
и 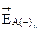 , а также векторов
, а также векторов 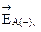 и
и 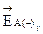 получаем векторы
получаем векторы 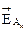 и
и 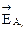 , которые являются соответственно горизонтальной и вертикальной составляющими вектора напряженности поля фазы А (с учетом ее зеркального отображения) в точке P.
, которые являются соответственно горизонтальной и вертикальной составляющими вектора напряженности поля фазы А (с учетом ее зеркального отображения) в точке P.
При этом, поскольку векторы 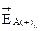 и
и 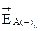 имеют противоположенные направления (рис. 2), модуль суммарного вектора
имеют противоположенные направления (рис. 2), модуль суммарного вектора 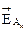 равен разности модулей этих векторов, В/м:
равен разности модулей этих векторов, В/м:
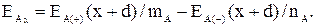 (3.7)
(3.7)
Модуль суммарного вектора 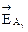 равен сумме модулей векторов
равен сумме модулей векторов 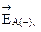 и
и 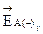 , В/м:
, В/м:
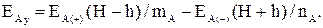 (3.8)
(3.8)
Подставим в выражение (3.8) зависимости (3.1) и (3.2):
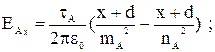 (3.9)
(3.9)
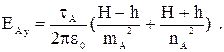 (3.10)
(3.10)
Поскольку мы рассматриваем воздушные линии электропередач переменного тока, заряд провода tAи напряженности EAxи EAyявляются синусоидальными функциями времени, т.е. их можно изображать комплексными величинами.
Линейный заряд фазы А определяется её емкостью и напряжением:
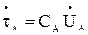 (3.11)
(3.11)
Подставим зависимость (3.11) в выражения (3.9) и (3.10):
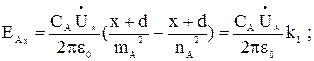 (3.12)
(3.12)
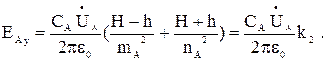 (3.13)
(3.13)
где CА – емкость фазы А относительно земли, Ф/м;
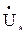 - комплекс напряжения фазы А относительно земли (эффективное значение фазного напряжения), В;
- комплекс напряжения фазы А относительно земли (эффективное значение фазного напряжения), В;
k1, k2, k3, k4, k5, k6 – коэффициенты, рассчитываемые по формулам:
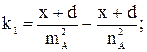
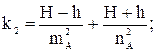
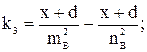
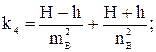
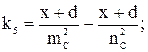
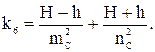
Отрезки m и n являются гипотенузами соответствующих прямоугольных треугольников (рис. 2) и определяются следующими выражениями:
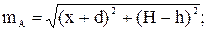
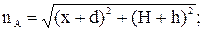
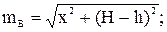
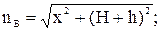
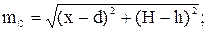

Аналогично находятся выражения для горизонтальных и вертикальных составляющих напряженностей фаз B и C:
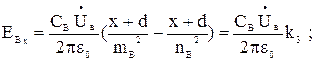 (3.14)
(3.14)
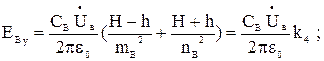 (3.15)
(3.15)
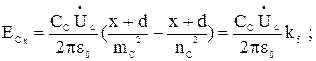 (3.16)
(3.16)
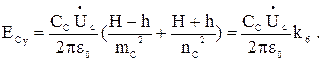 (3.17)
(3.17)
Горизонтальная и вертикальная составляющие напряженности суммарного поля В/м, т.е. обусловленные зарядами всех фаз линии и их зеркальных отображений, будут равны:
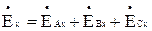 ; (3.18)
; (3.18)
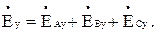 (3.19)
(3.19)
Подставляем в выражения (3.18) и (3.19) зависимости (3.12)-(3.17). При этом допускаем, что емкость всех фаз одинаковы:
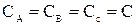 .
.
и трехфазная система напряжений симметрична:
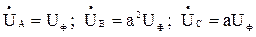 ,
,
где Uф - фазное напряжение линии, В;
a – фазовый оператор:
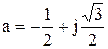 .
.
Учитывая выше сказанное, получаем:

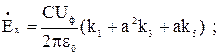 (3.20)
(3.20)
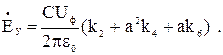 (3.21)
(3.21)
В действительной форме выражения (3.20) и (3.21) имеет вид:
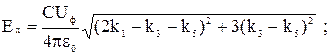 (3.22)
(3.22)
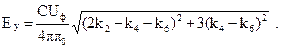 (3.23)
(3.23)
Искомая напряженность электрического поля трехфазной воздушной линии электропередачи:
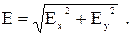 (3.24)
(3.24)
Подставив выражения (3.22) и (3.23) в (3.24), получим окончательное выражение напряженности электрического поля:
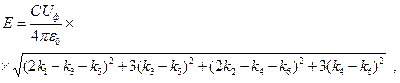
Емкость фазы трехфазной линии относительно земли на единицу длины линии:
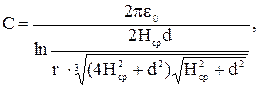 (3.25)
(3.25)
где Hср – средняя высота подвеса проводов над поверхностью земли, м.
При расщепленных фазах, состоящих из n проводов радиусом r0, и с расстоянием между ними (шаг расщепления) a, вместо r в формуле (3.25) учитывают эквивалентный радиус rэкв, м:
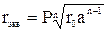 , (3.26)
, (3.26)
где P – поправочный коэффициент.
При n=2 и n=3 коэффициент P=1, а при n=4 P=1,09
Date: 2015-08-15; view: 2658; Нарушение авторских прав