Классификация видов моделирования

В зависимости от характера изучаемых процессов в системе все виды моделирования могут быть разделены на детерминированные и стохастические, статические и динамические, дискретные, непрерывные и дискретно – непрерывные.

Детерминированное моделирование отображает детерминированные процессы, т.е. процессы, в которых предполагается отсутствие всяких случайных воздействий; стохастическое моделирование отображает вероятностные процессы и события. В этом случае анализируется ряд реализаций случайного процесса и оцениваются средние характеристики, т.е. набор однородных реализаций.

Статическое моделирование служит для описания поведения объекта в какой либо момент времени, а динамическое моделирование отражает поведение объекта во времени.

Дискретное моделирование служит для описания процессов, которые предполагаются дискретными, соответственно непрерывное моделирование позволяет отразить непрерывные процессы в системах, а дискретно непрерывное моделирование используется для случаев, когда хотят выделить наличие как дискретных, так и непрерывных процессов.

При наглядном моделировании на базе представлений человека о реальных объектах создаются различные наглядные модели, отображающие явления и процессы, протекающие в объекте. В основу гипотетического моделирования исследователем закладывается некоторая гипотеза о закономерностях протекания процесса в реальном объекте, которая отражает уровень знаний исследователя об объекте и базируется на причинно-следственных связях между входом и выходом изучаемого объекта.

Гипотетическое моделирование используется, когда знаний об объекте недостаточно для построения формальных моделей.

Аналоговое моделирование основывается на применении аналогий различных уровней. Наивысшим уровнем является полная аналогия, имеющая место только для достаточно простых объектов. С усложнением объекта используют аналогии последующих уровней, когда аналоговая модель отображает несколько либо только одну сторону функционирования объекта. Символическое моделирование представляет собой искусственный процесс создания логического объекта, который замещает реальный и выражает основные свойства его отношений с помощью определенной системы знаков или символов.

Математическое моделирование. Для исследования характеристик процесса функционирования любой системы математическими методами, включая и машинные, должна быть проведена формализация этого процесса, т.е. построена математическая модель. Под математическим моделированием будем понимать процесс установления соответствия данному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать характеристики рассматриваемого реального объекта. Вид математической модели зависит как от природы реального объекта, так и задач исследования объекта и требуемой достоверности и точности решения этой задачи. Любая математическая модель, как и всякая другая, описывает реальный объект лишь с некоторой степенью приближения к действительности. Математическое моделирование для исследования характеристик процесса функционирования систем можно разделить на аналитическое, имитационное и комбинированное.

Для аналитического моделирования характерно то, что процессы функционирования элементов системы записываются в виде некоторых функциональных соотношений (алгебраических, интегро-дифференциальных, конечно-разностных и т.п.) или логических условий. Аналитическая модель может быть исследована следующими методами: а) аналитическим, когда стремятся получить в общем виде явные зависимости для искомых характеристик; б) численным, когда, не умея решать уравнений в общем виде стремятся получить числовые результаты при конкретных начальных данных; в) качественным, когда, не имея решения в явном виде, можно найти некоторые свойства решения (например, оценить устойчивость решения).

При имитационном моделировании реализующий модель алгоритм воспроизводит процесс функционирования системы во времени, причем имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры и последовательности протекания во времени, что позволяет по исходным данным получить сведения о состояниях процесса в определенные моменты времени, дающие возможность оценить характеристики системы. Основным преимуществом имитационного моделирования, по сравнению с аналитическим, является возможность решения более сложных задач. Имитационные модели позволяют достаточно просто учитывать такие факторы, как наличие дискретных и непрерывных элементов, нелинейные характеристики элементов системы, многочисленные случайные воздействия и др., которые часто создают трудности при аналитических исследовани-

ях. В настоящее время имитационное моделирование – наиболее эффективный метод исследования простых систем, а часто и единственный практически доступный метод получения информации о поведении системы, особенно на этапе ее проектирования.

Натурным моделированием называют проведение исследований на реальном объекте с последующей обработкой результатов эксперимента на основе теории подобия. При функционировании объекта в соответствии с поставленной целью удается выявить закономерности протекания реального процесса. Надо отметить, что такие разновидности натурного эксперимента, как производственный эксперимент и комплексные испытания, обладают высокой степенью достоверности. В процессе физического моделирования задаются некоторые характеристики внешней среды и исследуется поведение либо реального объекта, либо его модели при заданных или создаваемых искусственно воздействиях внешней среды.

Физическое моделирование может протекать в реальном и нереальном (псевдореальном) масштабах времени, а так же может рассматриваться без учета времени. В последнем случае изучению подлежат так называемые «замороженные» процессы, которые фиксируются в некоторый момент времени. Наибольшие сложность и интерес с точки зрения верности получаемых результатов представляет физическое моделирование в реальном масштабе времени.

63. Реляционная модель данных (Оля)

64. Количество информации и энтропия, кодирование информации

Количественная мера информации необходима для сравнения различных источников сообщений и каналов связей.

При введении меры информации абстрагируемся от конкретного смысла информации.

При ожидании сообщения существует неизвестность или неопределенность относительно того, что содержится в ожидаемом сообщении. Это сообщение уничтожает эту неопределенность. Значит, чем больше ликвидируется неопределенности, тем большее количество информации несет сигнал.

Неопределенность, которая ликвидируется приходом такого сигнала является единицей информации и называется – 1 бит.

С помощью такой единицы находим количество информации в более сложных случаях. Сложную операцию выбора одного состояния из нескольких сводят к последовательности элементарных операций выбора между двумя равновероятностными возможностями.

Рассмотрим случай, если все состояния сигнала имеют равные вероятности появления. Укажем в таблице количество состояний и соответствующее количество элементарных операций выбора

Легко заметить связь между значениями первого и второго столбцов. Обозначим через m – количество состояний сигнала, через I – количество элементарных операций выбора или количество информации. Тогда можно записать формулу:m = 2I. Выразим I через m, получим

формулу для вычисления количества информации, если все состояния сигнала равновероятностны:

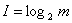
Вычислим по этой формуле количество информации для примеров 1 и 2, рассмотренных выше:

В первом примере:

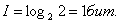
Во втором примере:

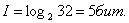
На практике неопределенность зависит не только от числа состояний сигнала, но и от вероятности реализации сигнала. Рассмотрим простой пример: в шахматы играют чемпион мира с перворазрядником. Сообщение о том, что выиграл чемпион, несет мало информации, т.к. это ожидаемое сообщение, вероятность выигрыша чемпиона велика. А вот сообщение о победе перворазрядника уничтожило больше неопределенности, вероятность такого исхода мала. Этот пример иллюстрирует необходимость учета вероятности появления каждого из состояний сигнала.

Выведем формулу вычисления количества информации для такого случая.

Пусть А и В –события или состояния сигнала. Количество информации I(A/B) заключается в сообщении события В относительно наступления А и равно значению выражения

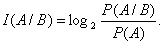
Числитель и знаменатель дроби – вероятности соответствующих событий.

Если появляется событие В=А, т.е. наступило А (значит А – достоверное событие), то I(A/B)= I(A/A)= I(A) – заключающееся в сообщении А. Учитывая, что А – достоверное событие, получим формулу для вычисления количества информации для сообщения А:

В дальнейшем основание логарифма указывать не будем.

Полученная формула

позволяет вычислить количество информации при получении сообщения (состояния), вероятность появления которого равна р.

Заметим, что для случая равновероятностных состояний можно пользоваться любой из этих двух формул.

3. Энтропия.

Энтропию (обозначение Нр), как меру неопределенности источника сообщений, осуществляющего выбор из m состояний, каждое из которых реализуется с вероятностью рi, предложил Клод Шеннон.

Энтропия вычисляется по формуле:

-logpi – количество информации, которое несет i- тое состояние сигнала есть величина случайная. Тогда, энтропия – это математическое ожидание информации, которое несет сигнал с m состояниями, каждое из которых имеет вероятность появления рi.

Энтропия позволяет сравнивать количества информации, приносимые различными сигналами.

4. Кодирование информации.

Для передачи и хранения информации используется код. Код имеет алфавит- набор символов и правила, по которым с помощью данного кода передается информация.

Известная со школьной скамьи десятичная позиционная система счисления – это способ кодирования натуральных чисел, декартовы координаты – способ кодирования геометрических объектов числами.

Алфавит может содержать любое количество символов. Простейший код состоит из двух символов (двоичный). Именно его используют в ЭВМ: алфавит состоит из 0 и 1. Примерами таких кодов являются азбука Морзе (точка и тире), светофор на железной дороге.

В общем случае, как уже отмечалось, символов может быть любое количество. В русском алфавите 32 буквы, т.е. 32 символа. Если учесть знаки препинания и пробелы, то символов становится больше.

Но разные символы применяются не одинаково часто. Например, в алфавите русского языка наиболее часто в текстах используются буквы а, о, и; самые редкие щ, э, ф. Следовательно, вероятности появления различных символов - различные. Возникает задача: создать наиболее экономичный код, т.е. такой код, у которого энтропия была бы наибольшей, т.е. наименьшим количеством символов передавать наибольшее количество информации.

Создавая коды, учитывают следующее: наибольшая энтропия соответствует сигналу (в нашем случае – коду), вероятности появления состояний которого одинаковы; простейшим является код из двух символов (выбор одного из двух равновероятностных состояний).

Код имеет следующие характеристики:

Экономичность- это отношение энтропии кода к максимальной энтропии в предположении, что все символы имеют одинаковую вероятность: Э =Н / Н мах;

Избыточность кода: И = 1 - Э. Данная характеристика показывает, какая часть символов лишняя и не несет информации.

Для оптимального кода экономичность близка к единице, а избыточность - к нулю.

Кроме экономичности и избыточности определяют цену кода, равную среднему числу битов на один символ (обозначение М(х)):

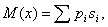
где pi – вероятность появления i- го символа в сообщении, si – длина кодовой последовательности, соответствующая i- му символу.

Рассмотрим примеры таких кодов.

Код Шеннона-Фэно.

Алгоритм построения кода:

1. Все символы записать в порядке не возрастания вероятностей.

2. Символы разбить на две группы с приближенно равными суммами вероятностей.

3. В левой группе символов коды начать с 0, в правой-с1.

4. Каждую группу снова разбить на две по такому же принципу и так же присвоить слева-0, справа-1.

5. Продолжать разбиения до тех пор,пока в каждой группе не останется по одному символу.

Алгоритм Хаффмена.

1. Все символы записать в порядке не возрастания вероятностей.

2. Объединить два редких символа в одну группу с вероятностью, равной сумме вероятностей этих символов.

3. Снова упорядочить список.

4. Повторять операции со второго шага, пока все символы не будут разбиты на две группы. В левой группе символов коды начать с 0, в правой- с1.

5. Затем работать с каждой группой следующим образом: отделять крайние символы, присваивая всегда слева 0, а справа-1, пока не будет закодирован каждый символ.

65. Тенденции построения современных графических систем: графическое ядро, приложения, инструментарий для написания приложений (Ваня Осипов)

66. Уровни представления данных (Нурсиня)

67. Средства моделирования и модели, применяемые в процессе проектирования АСОИУ (Настя Киселева)

68. Основные понятия исследования операций и системного анализа (=3)

69. Самосинхронизирующиеся коды (Мирош)

70. Стандарты в области разработки графических систем

Разрабатываемая графическая система должна соответствовать следующим стандартам и требованиям:

Инвариантность – обеспечивается на основе создания математических моделей геометрических объектов и алгоритмов их преобразований, инвариантных по отношению к проектируемым объектам. С точки зрения инвариантности относительно объекта проектирования можно выделить 4 уровня систем КГ:

1) Объектно-ориентированные, - в их функцию входит связь с проектирующими системами САПР.

2) Проблемно-ориентированные системы, - предназначены для реализации графических функций, типовых для данной проблемной ориентации.

3) Процедурно-ориентированные системы, - предназначены для реализации наиболее общих процедур графического ввода/вывода, не зависящих от проблемы и технических средств.

4) Приборно-ориентированные системы, - обеспечивают формирование вывода объекта на графическое устройство.

Принцип включения – обеспечивается возможность применения инвариантных программных средств САПР различных отраслей. Для этого проводится исследование требований к САПР в различных отраслях, затем определяются классы инвариантных геометрических задач конфигурирующих технических средств, состав системного обеспечения.

Принцип развития (не замкнутости) – достигается за счет модульности входящих в нее компонентов и оптимальности структуры системы, построенной на основе четкости деления на подсистемы.

Принцип информационного единства – достигается за счет использования универсальных структур данных для разработки проблемно-ориентированных языков описаний геометрических объектов, в синтаксисе которых используются общепринятые геометрические термины.

71. Понятия схемы и подсхемы данных

МЕСТАМИ ХУЙНЯ СОБАЧЬЯ

Схема представляет собой описание данных. По аналогии с уровнями описания данных можно выделить концептуальную, логическую и физическую схемы.

Подсхема данных – часть описания БД с учетом представления отдельного пользователя или логического проекта системы.

На самом высоком уровне имеется несколько внешних схем или подсхем, которые соответствуют разным представлениям данных. На концептуальном уровне описание базы данных называют концептуальной схемой, а на самом низком уровне абстракции - внутренней схемой.
Концептуальная схема описывает все элементы данных и связи между ними, с указанием необходимых ограничений поддержки целостности данных. Для каждой базы данных имеется только одна концептуальная схема. На нижнем уровне находится физическая схема, которая является полным описанием внутренней модели данных.
Она содержит определения хранимых записей, методы представления, описания полей данных, сведения об индексах и выбранных схемах хеширования. Для каждой базы данных существует только одна физическая схема.

В реляционных базах данных схема определяет таблицы, поля в каждой таблице (обычно с указанием их названия, типа, обязательности), и ограничения целостности (первичный, потенциальные и внешние ключи и другие ограничения).

Подсхема обычно описывается с учетом нужд прикладного программиста. Из подсхемы исключаются элементы схемы, к которым программист не должен иметь доступа.

72. Аналитическое моделирование

Для аналитического моделирования характерно, что процессы функционирования системы записываются в виде некоторых функциональных соотношений (алгебраических, дифференциальных, интегральных уравнений). Аналитическая модель может быть исследована следующими методами:

аналитическим, когда стремятся получить в общем виде явные зависимости для характеристик систем;

численным, когда не удается найти решение уравнений в общем виде и их решают для конкретных начальных данных;

качественным, когда при отсутствии решения находят некоторые его свойства.

Аналитические модели удается получить только для сравнительно простых систем. Для сложных систем часто возникают большие математические проблемы. Для применения аналитического метода идут на существенное упрощение первоначальной модели. Однако исследование на упрощенной модели помогает получить лишь ориентировочные результаты. Аналитические модели математически верно отражают связь между входными и выходными переменными и параметрами. Но их структура не отражает внутреннюю структуру объекта.

При аналитическом моделировании его результаты представляются в виде аналитических выражений. Например, подключив 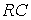-цепь к источнику постоянного напряжения

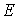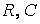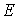( и - компоненты данной модели), мы можем составить аналитическое выражение для временной зависимости напряжения на конденсаторе :

(1.1)

Это линейное дифференциальное уравнение (ДУ) и является аналитической моделью данной простой линейной цепи. Его аналитическое решение, при начальном условии 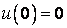, означающем разряженный конденсатор в момент начала моделирования, позволяет найти искомую зависимость – в виде формулы:

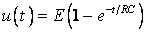(1.2)

Однако даже в этом простейшем примере требуются определенные усилия для решения ДУ (1.1) или для применения систем компьютерной математики (СКМ) с символьными вычислениями – систем компьютерной алгебры. 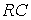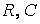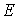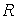Для данного вполне тривиального случая решение задачи моделирования линейной -цепи дает аналитическое выражение (1.2) достаточно общего вида – оно пригодно для описания работы цепи при любых номиналах компонентов и , и описывает экспоненциальный заряд конденсатора через резистор от источника постоянного напряжения .

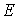Безусловно, нахождение аналитических решений при аналитическом моделировании оказывается исключительно ценным для выявления общих теоретических закономерностей простых линейных цепей, систем и устройств. Однако его сложность резко возрастает по мере усложнения воздействий на модель и увеличения порядка и числа уравнений состояния, описывающих моделируемый объект. Можно получить более или менее обозримые результаты при моделировании объектов второго или третьего порядка, но уже при большем порядке аналитические выражения становятся чрезмерно громоздкими, сложными и трудно осмысляемыми. Например, даже простой электронный усилитель зачастую содержит десятки компонентов. Тем не менее, многие современные СКМ, например, системы символьной математики Maple, Mathematica или среда MATLAB способны в значительной мере автоматизировать решение сложных задач аналитического моделирования.

Одной из разновидностей моделирования является численное моделирование, которое заключается в получении необходимых количественных данных о поведении систем или устройств каким-либо подходящим численным методом, таким как методы Эйлера или Рунге‑Кутта. На практике моделирование нелинейных систем и устройств с использованием численных методов оказывается намного более эффективным, чем аналитическое моделирование отдельных частных линейных цепей, систем или устройств. Например, для решения ДУ (1.1) или систем ДУ в более сложных случаях решение в аналитическом виде не получается, но по данным численного моделирования можно получить достаточно полные данные о поведении моделируемых систем и устройств, а также построить графики описывающих это поведение зависимостей.

73. Методологические основы теории принятия решений (=8)

74. Способы контроля правильности передачи информации (Лиза)

75. Технические средства компьютерной графики: мониторы, графические адаптеры, плоттеры, принтеры, сканеры

Мониторы.

Монитор (дисплей) является универсальным устройством вывода информации.

Классификация:

• ЭЛТ – на основе электронно-лучевой трубки (англ. cathode ray tube,

CRT);

• ЖК – жидкокристаллические мониторы (англ. liquid crystal display,

LCD);

• плазменный – на основе плазменной панели;

• проекционный – видеопроектор и экран, размещённые отдельно или объединённые в одном корпусе (как вариант – через зеркало или систему зеркал);

• OLED-монитор — на технологии OLED (англ. organic light-emitting diode – органический светоизлучающий диод);

• виртуальный ретинальный монитор – технология устройств вывода, формирующая изображение непосредственно на сетчатке глаза.

Основные параметры мониторов:

• вид экрана — квадратный или широкоформатный (прямоугольный);

• размер экрана — определяется длиной диагонали;

• разрешение — число пикселей по вертикали и горизонтали;

• глубина цвета — число отображаемых цветов (от монохромного до 32-битного);

• размер зерна или пикселя;

• частота обновления экрана;

• скорость отклика пикселей (не для всех типов мониторов).

Графические адаптеры.

Графический адаптер (видео карта) – устройство, преобразующее графический образ, хранящийся как содержимое памяти компьютера (или самого адаптера), в форму, пригодную для дальнейшего вывода на экран монитора.

Обычно видеокарта выполнена в виде печатной платы (плата расширения) и вставляется в разъём расширения, универсальный либо специализированный (AGP, PCI Express). Также широко распространены и встроенные (интегрированные) в системную плату видеокарты — как в виде отдельного чипа, так и в качестве составляющей части северного моста чипсета или ЦПУ; в этом случае устройство, строго говоря, не может быть названо видеокартой.

Видеокарта состоит из следующих частей: графический процессор, видеоконтроллер, видео-ПЗУ, видео-ОЗУ, ЦАП, коннектор и система охлаждения.

Плоттеры.

Графопостроитель, плоттер – устройство для автоматического вычерчивания с большой точностью рисунков, схем, сложных чертежей, карт и другой графической информации на бумаге размером до A0 или кальке.

Типы графопостроителей:

• рулонные и планшетные;

• перьевые, струйные и электростатические;

• векторные и растровые.

Назначение графопостроителей: высококачественное документирование чертёжно-графической информации.

Принтеры.

Принтер – устройство печати цифровой информации на твёрдый носитель, обычно на бумагу. Относится к терминальным устройствам компьютера. Процесс печати называется вывод на печать, а получившийся документ – распечатка или твёрдая копия.

Принтеры бывают струйные, лазерные, матричные и сублимационные; по цвету печати: чёрно-белые (монохромные) и цветные. Иногда из лазерных принтеров выделяют в отдельный вид светодиодные принтеры.

Сканеры.

Сканер – устройство, которое, анализируя какой-либо объект (обычно изображение, текст), создаёт цифровую копию изображения объекта. Процесс получения этой копии называется сканированием.

Сканеры бывают различных конструкций:

• ручной,

• планшетный,

• барабанный,

• проекционный.

Изображение всегда сканируется в формат RAW – а затем конвертируется в обычный графический формат с применением текущих настроек яркости, контрастности, и т. д. Эта конвертация осуществляется либо в самом сканере, либо в компьютере – в зависимости от модели конкретного сканера. На параметры и качество RAW-данных влияют такие аппаратные настройки сканера, как время экспозиции матрицы, уровни калибровки белого и чёрного, и т. п.

76. Классификация информационно-вычислительных сетей (=5)

77. Планирование имитационных экспериментов с моделями (Ира)

78. Задачи выбора решений (=13)

79. Способы конструирования и верификации программ

Способы конструирования программ:

Псевдокод — это искусственный и неформальный язык, который помогает программисту разрабатывать алгоритмы. Псевдокод используется для разработки алгоритмов, которые потом должны быть преобразованы в структурированную программу на C++. Псевдокод подобен разговорному языку; он удобный и дружелюбный, но это не язык программирования. Программы на псевдокоде не могут выполняться на компьютере. Их назначение — помочь программисту «обдумать программу» прежде, чем по­пытаться написать ее на таком языке программирования, как C++. Тщательно подго­товленная программа на псевдокоде может быть легко преобразована в соот­ветствующую программу на C++. Во многих случаях для этого достаточно просто заменить предложения псевдокода их эквивалентами в языке С++. Псевдокод включает только исполняемые операторы — те, которые вы­полняются, когда программа переведена из псевдокода на C++ и запущена на счет. Объявления не являются исполняемыми операторами.

Блок-схема — это графическое представление алгоритма или фрагмента алгоритма. Блок-схема рисуется с использованием специальных символов, таких, как прямоугольники, ромбы, овалы и малые окружности; эти символы соединяются стрелками, называемыми линиями связи. Подобно псевдокоду блок-схемы часто используются при разработке и описании алгоритмов, хотя большинство программистов предпочитает псевдокод. Блок-схемы наглядно показывают, как действуют управляющие структуры.

Нисходящее проектирование – подход к проектированию программ, при котором первоначально создается главный модуль, для которого затем проводится декомпозиция (разбиение на модули, решающие подзадачи главной задачи).

Восходящее проектирование. Иногда основному проектированию сверху-вниз сопутствует разработка компонент проекта снизу-вверх. Разработка начинается от компонента нижнего уровня, далее переходят к разработке компонента следующего уровня иерархии и т.д. Достоинством этого принципа является то, что при переходе к разработке компонентов более высокого уровня иерархии компоненты проекта нижних уровней можно считать готовыми и подключать их к проектируемым компонентам верхнего уровня.

Часто оба метода применяются одновременно:

Сверху-вниз: при объединении в единое целое;

Снизу-вверх: при разработке общих хорошо отлаженных блоков.

Способы верификации программ:

Верификация (подтверждение правильности) – состоит в проверке и доказательстве корректности разработанной программы по отношению к совокупности формальных утверждений, представленных в спецификации и полностью определяющей связь между входными и выходными данными этой программы. При этом отношения между переменными н входе и выходе программы анализируется не в виде значений, как при тестировании, а в виде описаний их свойств, проявляющихся при любых процессах обработок этих переменных контролируемой в программе.

Верификация программы в принципе исключает необходимость её тестирования и отладки, так как при этом на более высоком уровне понятий и описаний всех переменных, устанавливается корректность процессов, их обработка и преобразования.

Для доказательства частичной правильности используется метод индуктивных утверждений, сущность которого состоит в следующем. Пусть утверждение связано с началом программы, 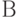- с конечной точкой программы и утверждение отражает некоторые закономерности значений переменных, по крайней мере, в одной из точек каждого замкнутого пути в программе (например, в циклах). Если при выполнении программа попадает в 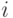-ю точку и справедливо утверждение , а затем она проходит от точки 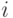к точке , то будет справедливо утверждение .

Теорема 6.1. Если выполнены все действия метода индуктивных утверждений для программы, то она частично правильна относительно утверждений , , .

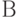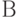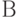Требуется доказать что, если выполнение программы закончится, то утверждение будет справедливым. По индукции, при прохождении точек программы, в которых утверждение будет справедливым, то и -я точка программы будет такой же. Таким образом, если программа прошла -точку и утверждения и справедливы, то тогда, попадая из -ой точки в точку, утверждение будет справедливым, что и требовалось доказать.

Метод Флойда основан на определении условий для входных и выходных данных и в выборе контрольных точек в доказываемой программе так, чтобы путь прохождения по программе пересекал хотя бы одну контрольную точку. Для этих точек формулируются утверждения о состоянии и значениях переменных в них (для циклов эти утверждения должны быть истинными при каждом прохождении цикла инварианта).

Каждая точка рассматривается для индуктивного утверждения того, что формула остается истинной при возвращении в эту точку программы и зависит не только от входных и выходных данных, но и от значений промежуточных переменных. На основе индуктивных утверждений и условий на аргументы создаются утверждения с условиями проверки правильности программы в отдельных ее точках. Для каждого пути программы между двумя точками устанавливается проверка на соответствие условий правильности и определяется истинность этих условий при успешном завершении программы на данных, удовлетворяющих входным условиям.

Метод Хоара - это усовершенствованный метод Флойда, основанный на аксиоматическом описании семантики языка программирования исходных программ. Каждая аксиома описывает изменение значений переменных с помощью операторов этого языка. Формализация операторов перехода и вызовов процедур обеспечивается с помощью правил вывода, содержащих индуктивные высказывания для каждой точки и функции исходной программы.

Система правил вывода дополняется механизмом переименования глобальных переменных, условиями на аргументы и результаты, а также на правильность задания данных программы. Оператор перехода трактуется как выход из циклов и аварийных ситуаций.

Описание с помощью системы правил утверждений - громоздкое и отличается неполнотой, поскольку все правила предусмотреть невозможно. Данный метод проверялся экспериментально на множестве программ без применения средств автоматизации из-за их отсутствия.

Метод Маккарти состоит в структурной проверке функций, работающих над структурными типами данных, структур данных и диаграмм перехода во время символьного выполнения программ. Эта техника включает в себя моделирование выполнения кода с использованием символов для изменяемых данных. Тестовая программа имеет входное состояние, данные и условия ее выполнения.

Выполняемая программа рассматривается как серия изменений состояний. Самое последнее состояние программы считается выходным состоянием и если оно получено, то программа считается правильной. Данный метод обеспечивает высокое качество исходного кода.

Метод Дейкстры предлагает два подхода к доказательству правильности программ. Первый подход основан на модели вычислений, оперирующей с историями результатов вычислений программы, анализом путей прохождения и правил обработки большого объема информации. Второй подход базируется на формальном исследовании текста программы с помощью предикатов первого порядка. В процессе выполнения программа получает некоторое состояние, которое запоминается для дальнейших сравнений.

Основу метода составляет математическая индукция, абстрактное описание программы и ее вычисление. Математическая индукция применяется при прохождении циклов и рекурсивных процедур, а также необходимых и достаточных условий утверждений. Абстракция позволяет сформулировать некоторые количественные ограничения. При вычислении на основе инвариантных отношений проверяются на правильность границы вычислений и получаемые результаты.

80. Способы коммутации в сетях (Лиза)

81. Оценка точности и достоверности результатов моделирования

Обработка результатов имитационных экспериментов принципиально не может дать точных значений (т.к. моделируются случайные процессы, и мы можем их только как-то оценить). Существует некая степень точности результатов - приближение к какому-то истинному значению. И эта степень точности в значительной мере определяется размером выборки (количеством реализаций).

Задача определения такого размера выборки, который позволяет обеспечить желаемый уровень точности и в то же время минимальную стоимость моделирования, весьма трудна, но и весьма важна.

Число испытаний N определяет точность получаемых результатов моделирования. Если необходимо оценить величину случайного параметра Х по результатам моделирования x1, x2, … xn, то за оценку следует брать величину хср. Но из-за случайности хср будет отличаться от истинного значения параметра Х

а если мы зададимся какой-то точностью оценки (назовем ее - e), то должно выполняться неравенство:

|Х-хср|<e

e - точность оценки величины случайного параметра Х; (половина ширины доверительного интервала)

хср - среднее значение результатов моделирования x1, x2, … xn.

Вероятность того, что данное неравенство выполняется, называют уровнем значимости или доверительной вероятностью:

P(|Х-xср|<e)=a

a - уровень значимости, доверительная вероятность, (1-a) - достоверность.

Это выражение и берется за основу при определении точности результатов статистических испытаний, т.е. результатов имитационных экспериментов.

α и ε - задаем сами.

Определение количества реализаций для оценки вероятности наступления события.

Отклики моделей обычно одно из двух состояний, например успех - неудача. Такие отклики называют переменными Бернулли. Они характеризуются биномиальным распределением.

Пусть целью моделирования будет определение вероятности наступления некоторого события А, определяющего какое-то состояние моделируемой системы. В любой из реализаций процесс наступления события А является случайной величиной, которая может приобретать значение x1=1 с вероятностью р (т.е. событие наступило) и x2=0 с вероятностью 1-р.

На основе центральной предельной теоремы, можно найти количество реализаций для оценки вероятности наступления события с заданным уровнем значимости и точностью.

Центральная предельная теорема: распределение суммы независимых наблюдений n различных СВ стремится к нормальному, при n®¥, независимо от характера распределения СВ.

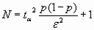
ta - квантиль нормального распределения вероятностей. Находится из специальных таблиц распределения Стьюдента (t-распределение) на основе заданного уровня значимости и определенных степеней свободы.

Число степеней свободы: ν = k - 1 - m, (k - число значений или интервалов СВ; т - число определяемых параметров).

Для определения вероятности р делают пробные испытания (N= 50…100) и получают частоту m/N, после чего определяют конечное количество испытаний.

р =m/N

Определение количества реализаций для оценки среднего значения случайной величины.

Случайная величина имеет математическое ожидание m и дисперсию s2.

На основе центральной предельной теоремы количество реализаций N для оценки среднего значения случайной величины будет

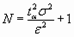
Величину σ нужно либо знать, либо для ее определения нужно провести пробный эксперимент и найти ее оценку.

Если мы имеем представление о пределах, в которых может изменяться отклик системы, то грубую оценку величины σ можно получить из условия, что размах переменной отклика равен примерно 4σ: Если известен разумный размах переменной отклика - d, то σ=d/4.

Для определения оценки s2 проводят 50…100 испытаний и определяют по формуле:

82. Функции полезности и критерии при принятии решений (17 – первый вариант)

Полезность – некоторое число, приписываемое лицом, принимающим решение, каждому возможному исходу. Функция полезности Неймана-Моргенштерна для лица, принимающего решение, (ЛПР) показывает полезность, которую он приписывает каждому возможному исходу. У каждого ЛПР своя функция полезности, которая показывает его предпочтение тем или иным исходам в зависимости от его отношения к риску.

В Задачах Принятия Решений (ЗПР) значение функции полезности выражает предпочтения, полезность альтернатив. Она может быть оценена на множестве альтернатив и на множестве критериев, при этом критерии могут быть взаимно независимыми и зависимыми.

Решение задачи выбора оптимального действия полностью определяется двумя факторами: 1) типом и объемом информации о состояниях и 2) критерием оптимальности альтернативы. Собственно говоря, критерий оптимальности также зависит от имеющейся информации о состояниях. Поясним более детально, что подразумевается под понятием информации о состояниях Информация о состояниях отражает степень уверенности в том, какое состояние будет в действительности иметь место, или степень уверенности, что одно состояние более вероятно по сравнению с другим. В то же время, множество самих состояний является известным. Информация о состояниях существенно влияет на решение задачи. Так, например, если с уверенностью 100% известно, что будет иметь место быстрый подъем экономики, то очевидно, что покупка акций предприятия даст наибольший доход. Рассмотренная ситуация является наиболее простой и приводит к принятию решений в условиях полной определенности. Другим крайним случаем является отсутствие какой-либо информации о состояниях. В этой ситуации имеет место задача принятия решений в условиях неопределенности. Это редкий случай, так как обычно, исходя из предыдущего опыта или наблюдений, а также текущих тенденций, можно с некоторой вероятностью говорить о будущих состояниях.

Каждая задача принятия решений имеет свой критерий оптимальности, т.е. некоторое правило, по которому численно определяется условие предпочтения одного действия по отношению к другому. Критерий оптимальности определяет упорядочивание всех альтернатов (множества А) по предпочтению.

При этом, как уже было сказано, критерий оптимальности полностью зависит от информации о состояниях.

Принятие решений в условиях определенности характеризуется однозначной или детерминированной связью между принятым решением и его результатом. Это наиболее простой класс задач принятия решений, когда состояние, которое будет определённо иметь место, известно заранее, т.е. до выполнения действия. ЛПР в данном случае может всегда точно предсказать последствия от выбора каждого действия. Это фактически означает, что число состояний сводится к одному, т.е. m = 1.

Поэтому логично потребовать от рационального лица, принимающего решение, выбрать то действие, которое дает наибольшее значение функции полезности.

В условиях неопределенности лицо, принимающее решение, не может сказать что-либо о возможных состояниях, т.е. абсолютно неизвестно, какое из состояний будет иметь место. Для решения данной задачи наиболее распространенными критериями принятия решений являются:

1) критерий равновозможных состояний (критерий Лапласа):

2) критерий максимина Вачьда:

3) критерий пессимизма-оптимизма Гурвица;

4) критерий минимакса сожалений Сэвиджа.

Следует отметить, что приведенные критерии являются далеко не единственными для принятия решений в условиях неопределенности. Однако остальные критерии являются в основном комбинацией этих критериев.

83. Универсальные ОС и ОС специального назначения (=26, Оля)

84. Модульные программы, пример.

Модульное программирование основано на понятии модуля - логически взаимосвязанной совокупности функциональных элементов, оформленных в виде отдельных программных модулей/

Модуль характеризуют:

один вход и один выход - на входе программный модуль получает определенный набор исходных данных, выполняет содержательную обработку и возвращает один набор результатных данных, т.е. реализуется стандартный принцип IPO (Input - Process - Output) - вход-процесс-выход;

функциональная завершенность – модуль выполняет перечень регламентированных операций для реализации каждой отдельной функции в полном составе, достаточных для завершения начатой обработки;

логическая независимость - результат работы программного модуля зависит только от исходных данных, но не зависит от работы других модулей;

слабые информационные связи с другими программными модулями - обмен информацией между модулями должен быть по возможности минимизирован;

обозримый по размеру и сложности программный элемент.

Программная система обычно является большой, поэтому принимаются меры для ее упрощения. Для этого такую программу разрабатывают по частям, которые называются программными модулями. Программный модуль - это любой фрагмент описания процесса, оформляемый как самостоятельный программный продукт, пригодный для использования в описаниях процесса. Это означает, что каждый программный модуль программируется, компилируется и отлаживается отдельно от других модулей программы, и тем самым, физически разделен с другими модулями программы. Каждый разработанный программный модуль может включаться в состав разных программ, если выполнены условия его использования, декларированные в документации по этому модулю. Таким образом, программный модуль может рассматриваться и как средство борьбы со сложностью программ, и как средство борьбы с дублированием в программировании.

Date: 2015-08-15; view: 810; Нарушение авторских прав