Задачи для самостоятельного решения. Задача 1. Человек массой 60 кг, бегущий со скоростью 8 км/ч, догоняет тележку массой 80 кг, движущуюся со скоростью 2,9 км/ч

Задача 1. Человек массой 60 кг, бегущий со скоростью 8 км/ч, догоняет тележку массой 80 кг, движущуюся со скоростью 2,9 км/ч, и вскакивает на нее. 1) С какой скоростью станет двигаться тележка? 2) С какой скоростью будет двигаться тележка, если человек бежал ей навстречу?

Задача 2. Конькобежец массой 70 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой 3 кг со скоростью 8 м/с. Найти, на какое расстояние откатится при этом конькобежец, если известно, что коэффициент трения коньков о лед равен 0,02.

Задача 3. Человек, стоящий на неподвижной тележке, бросает вперед в горизонтальном направлении камень массой 2 кг. Тележка с человеком покатилась назад, и в первый момент после бросания ее скорость была равна 0,1 м/с. Масса тележки с человеком равна 100 кг. Найти кинетическую энергию брошенного камня через 0,5 с после начала его движения. Сопротивлением воздуха при полете камня пренебречь..

Задача 4. Люстра массой 100 кг подвешена к потолку на металлической цепи, длина которой 5 м. Какова высота, на которую можно отклонить люстру, чтобы при последующих качаниях цепь не оборвалась, если известно, что разрыв наступает при силе натяжения 2 кН?

Задача 5. Радиус вала махового колеса r=10^-2 м. На вал намотан шнур, к концу которого привязан груз массой m=0,2 кг. Под действием силы тяжести груз опускается за t=5 с с высоты h₁=1,2 м, а затем, вследствие вращения колеса, по инерции поднимается на высоту h₂=0,8 м. Определить момент инерции колеса.

Задача 6. Горизонтальная платформа массой 80 кг и радиусом 1 м вращается с угловой скоростью, соответствующей 20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. Какое число оборотов в минуту будет делать платформа, если человек, опустив руки, уменьшить свой момент инерции от 2,94 кг∙м² до 0,98 кг∙м²? Считать платформу круглым однородным диском.

Задача 7. Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой n ₁ = 10 об/мин. Человек массой m ₀ = 60 кг стоит при этом на краю платформы. С какой частотой n ₂ начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека - материальной точкой.

Задача 8. Математический маятник массы m ₁ и стержень массы m ₂ подвешены в одной и той же точке А, вокруг которой они могут свободно колебаться. Длина нити маятника равна длине нити стержня. Шарик маятника отклоняют в сторону так, что он приподнимается на высоту h относительно своего нижнего положения. Затем шарик отпускают, и он неупруго сталкивается со стержнем. Как будут двигаться шарик и нижний конец стержня после удара и на какие высоты они поднимутся?

Задача 9. Блоки радиусами r ₁ и r ₂ (рис.7) жестко скреплены между собой и насажены на общую ось. Грузы 1 и 2 массами m ₁ и m ₂, разматывая нити, намотанные на блоки, приводят их во вращение. Пренебрегая массой нитей и считая блоки однородными дисками массами М ₁ и М ₂ соответственно, определить, через сколько времени скорость груза 1 станет равной v ₁, если движение начинается из состояния покоя и при вращении на блоки действует постоянный момент сил сопротивления М.

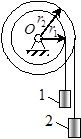
Рис.7

Задача 10. Блоки (рис.8) радиусами r ₁ и r ₂ жестко скреплены между собой и насажены на общую ось. Груз 2 массы m ₂, разматывая намотанную на блок нить, приводит блоки во вращение и поднимает груз 1 массы m ₁. Считая, что на блоки действует момент сил сопротивления 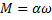, где 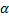– постоянная, определить угловую скорость вращения блоков, если движение начинается из состояния покоя. Блоки считать однородными дисками массами М ₁ и М ₂ соответственно, массой нитей пренебречь.

Рис.8

Задача 11. Груз 1 массы m ₁ (рис.9) поднимается посредством каната, навитого на барабан 2, к которому приложен постоянный вращающий момент М. Барабан 2 представляет собой однородный цилиндр радиуса r и массы m ₂. 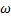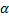Определить угловую скорость вращения барабана как функцию времени, если движение начинается из состояния покоя, а при вращении возникает момент M ₁ сил сопротивления, пропорциональный угловой скорости , , где – постоянная.

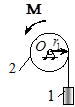
Рис.9

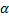Задача 12. Груз 1 массы m (рис.10) поднимается при помощи ворота, на который действует момент сопротивления, пропорциональный угловой скорости его вращения, , где – постоянная. Масса барабана ворота равна m ₁, радиус барабана r, длина рукоятки ОА = l. Считая силу F, приложенную перпендикулярно к рукоятке ОА, постоянной по величине, определить закон движения груза 1, если в начальный момент он покоился. Барабан считать однородным цилиндром, массой рукоятки пренебречь.

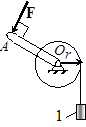
Рис.10

Задача 13. Груз 1 массы m ₁ (рис.11) из состояния покоя поднимают вверх по шероховатой наклонной плоскости посредством веревки, намотанной на барабан 2, к которому приложен вращающий момент М = at, где a – постоянная. Определить закон движения груза 1, если коэффициент трения тела 1 о плоскость равен f, а угол наклона плоскости к горизонту 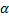, причем при t = 0 груз покоился. Кроме того, определить момент времени, когда груз 1 начнет движение. Барабан считать однородным цилиндром радиуса r и массы m.

Рис.11

Задача 14. Два блока массами m ₁ и m ₂ (рис.12) и соответственно радиусами r ₁ и r ₂ жестко соединены между собой и насажены на общую ось вращения О. К концу одной веревки, намотанной на блок, прикреплен груз А массы m, поднимаемый по шероховатой наклонной плоскости с углом 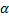наклона к горизонту. К концу другой веревки приложена постоянная сила F. Считая блоки однородными дисками и полагая, что коэффициент трения скольжения равен f, а весом веревок и трением в блоках можно пренебречь, определить зависимость угловой скорости вращения от времени, если движение началось из состояния покоя.

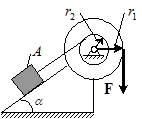
Рис.12

Задача 15. Блоки радиусами r ₁ и r ₂ (рис.13) жестко скреплены между собой и насажены на общую ось. Грузы 1 и 2 массами m ₁ и m ₂, разматывая нити, намотанные на блоки, приводят их во вращение. Пренебрегая массой нитей и считая блоки однородными дисками массами М ₁ и М ₂ соответственно, определить угловое ускорение блоков, если при вращении на блоки действует момент сил сопротивления М = at, где a – постоянная, а также момент времени, когда система под действием сил сопротивления остановится, если движение начинается из состояния покоя.

Рис.13

Задача 16. Груз 1 массы m ₁, (рис.14) опускаясь вертикально вниз, раскручивает ступенчатый блок 2 посредством невесомой и нерастяжимой нити, которая намотана на колесо блока радиуса r ₁. На большее колесо блока, имеющее радиус r ₂, намотана другая нить, второй конец которой привязан к грузу 3 массы m, скользящему по наклонной плоскости с коэффициентом трения скольжения, равным f, и углом наклона 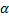. Блок состоит из однородных дисков массам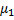и и 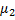соответственно, жестко соединенных друг с другом и имеющих общую ось вращения. Определить угловую скорость блока 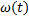и его угловое ускорение, если движение начинается из состояния покоя.

Рис.14

Задача 17. Груз 1 массы m ₁ (рис.15) из состояния покоя скользит вниз по шероховатой наклонной плоскости и посредством невесомой нити раскручивает барабан 2, на который действует момент сил сопротивления M, пропорциональный угловой скорости барабана, 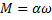, где a – постоянная. Определить угловую скорость барабана как функцию времени и ускорение груза 1, если коэффициент трения тела 1 о плоскость равен f, а угол наклона плоскости к горизонту 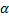. Барабан считать однородным цилиндром радиуса r и массы m.

Рис.15

Задача 18. Блоки радиусами r ₁ и r ₂ (рис.16) жестко скреплены между собой и насажены на общую ось. Груз 2 массы m ₂, разматывая намотанную на блок нить, приводит блоки во вращение и поднимает груз 1 массы m ₁. Считая, что на блоки действует момент сил сопротивления М = at, где a – постоянная, определить угловое ускорение блоков, а также момент времени, когда система под действием сил сопротивления остановится, если движение начинается из состояния покоя. Блоки считать однородными дисками массами М ₁ и М ₂ соответственно, массой нитей пренебречь.

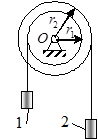
Рис.16

Задача 19. Груз 1 массы m ₁ (рис.17), падая по вертикали, раскручивает ступенчатый блок 2 посредством невесомой и нерастяжимой нити, которая намотана на колесо блока радиуса r ₁. На меньшее колесо A блока, имеющее радиус r ₂, намотана другая нить, второй конец которой привязан к грузу 3 массы m, скользящему по горизонтальной плоскости с коэффициентом трения скольжения, равным f. Блок состоит из однородных дисков массам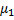и и 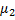соответственно, жестко соединенных друг с другом и имеющих общую ось вращения. При вращении блока на него действует постоянный момент сил сопротивления М. Определить угловую скорость вращения блока как функцию времени и ускорение груза 3, если движение начинается из состояния покоя.

Рис.17

Задача 20. Груз 1 массы m ₁ (рис.18) из состояния покоя поднимают вверх по шероховатой наклонной плоскости посредством веревки, намотанной на барабан 2, к которому приложен вращающий момент М = at ², где a – постоянная. Определить зависимость угловой скорости барабана от времени, если коэффициент трения тела 1 о плоскость равен f, а угол наклона плоскости к горизонту 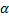, причем при t = 0 груз покоился. Кроме того, определить момент времени, когда груз 1 начнет движение. Барабан считать однородным цилиндром радиуса r и массы m.

Рис.18

Задача 21. Блоки радиусами r ₁ и r ₂ (рис.19) жестко скреплены между собой и насажены на общую ось. Груз 2 массы m ₂, разматывая намотанную на блок нить, приводит блоки во вращение и поднимает груз 1 массы m ₁. Считая, что на блоки действует постоянный момент сил сопротивления М, определить скорость груза 1 как функцию времени t, если движение начинается из состояния покоя. Блоки считать однородными дис­ками массами М ₁ и М ₂ соответственно. Массой нитей пренебречь.

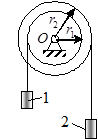
Рис.19

Задача 22. К грузам А и В массами m ₁ и m ₂ (рис.20) соответственно прикреплены нерастяжимые нити, вторые концы которых намотаны на однородные диски 1 и 2 массами 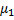, 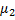и радиусами r ₁ и r ₂ (r ₂ > r ₁). Диски жестко соединены между собой и насажены на общую ось. Груз А, спускаясь по наклонной плоскости с углом 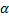наклона к горизонту, раскручивает диски и поднимает груз В вверх по наклонной плоскости с углом . Определить угловую скорость вращения блока как функцию времени и ускорение груза А. Силами трения и массой нитей пренебречь, движение начинается из состояния покоя.

Рис.20

Задача 23. Груз 1 массы m ₁, (рис.21) скользящий под действием постоянной горизонтальной силы F по горизонтальной плоскости с коэффициентом трения скольжения f, раскручивает ступенчатый блок 2 посредством невесомой и нерастяжимой нити, которая намотана на колесо блока радиуса r ₁. На большее колесо блока, имеющее радиус r ₂, намотана другая нить, второй конец которой привязан к грузу 3 массы m. Блок состоит из однородных дисков массам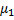и и 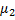соответственно, жестко соединенных друг с другом и имеющих общую ось вращения. Определить угловую скорость вращения блока как функцию времени и ускорение груза 3, если движение начинается из состояния покоя.

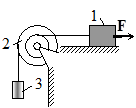
Рис.21

Задача 24. Груз 1 массы m ₁ (рис.22) поднимается посредством каната, навитого на барабан 2, к которому приложен вращающий момент М = at, где a – постоянная. В начальные моменты времени, из-за малости величины вращающего момента, груз будет опускаться и лишь с некоторого момента времени начнет подниматься. Полагая, что движение начинается из состояния покоя, определить угловую скорость вращения барабана как функцию времени, а также момент времени, когда система остановится и барабан начнет вращаться в другую сторону. Барабан 2 считать однородным цилиндром радиуса r и массы m ₂.

Рис.22

Задача 25. Груз 1 массы m (рис.23) поднимается при помощи ворота (жестко соединенных барабана и стержня), на который действует момент сил сопротивления M ₁ = at, где a – постоянная. Масса барабана ворота равна m ₁, радиус барабана r, длина рукоятки ОА = l. Считая, что сила F приложена перпендикулярно к рукоятке ОА и постоянна по величине, определить закон движения груза 1 и момент времени, когда он остановится, если в начальный момент груз покоился. Барабан считать однородным цилиндром, массой рукоятки пренебречь.

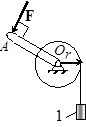
Рис.23

Задача 26. Два блока массами m ₁ и m ₂ (рис.24) и радиусами r ₁ и r ₂ соответственно жестко соединены между собой и насажены на общую ось вращения О. К концу одной веревки, намотанной на блок, прикреплен груз А массы m, поднимаемый по наклонной плоскости с углом 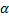наклона к горизонту и с коэффициентом трения f. К концу другой веревки приложена сила F = at, где a – постоянная. Считая, что блоки являются однородными дисками, а весом веревок и трением в блоках можно пренебречь, определить зависимость угловой скорости вращения от времени, если движение началось из состояния покоя. Кроме того, определить момент времени, когда груз А начнет движение.

Рис.24

Задача 27. Груз 1 массы m ₁ (рис.25), опускаясь вертикально вниз, раскручивает ступенчатый блок 2 посредством невесомой и нерастяжимой нити, которая намотана на колесо блока радиуса r ₁. На большее колесо блока, имеющее радиус r ₂, намотана другая нить, второй конец которой привязан к грузу 3 массы m, скользящему по гладкой наклонной плоскости с углом наклона 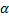. Блок состоит из однородных дисков массам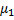и и 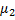соответственно, жестко соединенных друг с другом и имеющих общую ось вращения, причем при вращении на блок действует момент сил сопротивления М = at, где a – постоянная. Определить угловую скорость блока 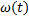и момент его вторичной остановки, если движение начинается из состояния покоя.

Рис.25

Задача 28. Однородный горизонтальный диск (рис.26) радиуса r и массы m может вращаться вокруг проходящей через его центр О вертикальной оси. Вдоль радиуса ОА по направляющей может двигаться точечное тело А массы m ₀. В начальный момент времени к диску приложили вращающий момент M = αt, где α – постоянная, а тело А начало двигаться от точки О с постоянной относительной скоростью v_r = v ₀. Определить зависимость угловой скорости вращения и ее величину, когда тело А достигнет края диска.

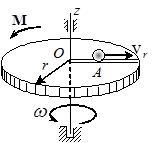
Рис.26

Задача 29. Груз 1 массы m ₁ (рис.27) поднимается посредством каната, навитого на барабан 2, к которому приложен вращающий момент М = at ², где a – постоянная. В начальные моменты времени, из-за малости величины вращающего момента, груз будет опускаться и лишь с некоторого момента времени начнет подниматься. Полагая, что движение начинается из состояния покоя, определить угловую скорость вращения барабана как функцию времени, а также момент времени, когда система остановится и барабан начнет вращаться в другую сторону. Барабан 2 считать однородным цилиндром радиуса r и массы m ₂.

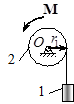
Рис.27

Задача 30. К грузам А и В (рис.28) массами m ₁ и m ₂ соответственно прикреплены нерастяжимые нити, вторые концы которых намотаны на однородные диски 1 и 2 массами 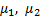и радиусами r ₁ и r ₂ (r ₂ > r ₁). Диски жестко соединены между собой и насажены на общую ось. Груз B, спускаясь по наклонной плоскости с углом наклона к горизонту, раскручивает диски и поднимает груз A вверх по наклонной плоскости с углом 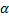, при этом на блок действует постоянный момент сил сопротивления М. Определить угловую скорость вращения блока как функцию времени и ускорение груза В. Силами трения и массой нитей пренебречь, движение начинается из состояния покоя.

Рис.28

Задача 31. Блоки радиусами r ₁ и r ₂ (рис.29) жестко скреплены между собой и насажены на общую ось. Грузы 1 и 2 массами m ₁ и m ₂, разматывая нити, намотанные на блоки, приводят их во вращение. Пренебрегая массой нитей и считая блоки однородными дисками массами М ₁ и М ₂ соответственно, определить скорость груза 2 как функцию времени, если движение начинается из состояния покоя и при вращении на блоки действует момент сил сопротивления 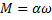, где α – постоянная.

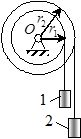
Рис.29

Задача 32. Барабан 1 (рис.30) массы m ₁ и радиуса r приводится во вращение посредством груза 2 массы m ₂, привязанного к концу нерастяжимого троса. Трос переброшен через идеальный блок 3 и намотан на барабан 1. При вращении барабана появляется момент сил сопротивления M, пропорциональный времени, M = αt, где α – постоянная. Полагая, что движение начинается из состояния покоя, определить зависимость угловой скорости барабана от времени и момент времени, когда система снова остановится. Барабан считать однородным цилиндром, массой каната пренебречь.

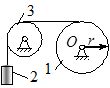
Рис.30

Задача 33. Груз 1 (рис.31) массы m ₁, опускаясь вертикально вниз, раскручивает ступенчатый блок 2 посредством невесомой и нерастяжимой нити, которая намотана на колесо блока радиуса r ₁. На большее колесо блока, имеющее радиус r ₂, намотана другая нить, второй конец которой привязан к грузу 3 массы m, скользящему по гладкой наклонной плоскости с углом наклона 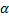. Блок состоит из однородных дисков массам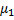и и 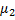соответственно, жестко соединенных друг с другом, причем при вращении на блок действует момент сил сопротивления М = at ², где a – постоянная. Определить скорость v ₁(t) груза 1 и момент его остановки, если движение начинается из состояния покоя.

Рис.31

Задача 34. Шкив М (рис.32), вращающийся с угловой скоростью , тормозится при помощи ручного тормоза АВ. Сила, с которой давят на ручку тормоза, F = at, где a – постоянная. Считая шкив однородным диском радиуса r, определить, через какое время шкив остановится и сколько он совершит оборотов, если коэффициент трения между тормозом и шкивом f, длина рукоятки АВ = l, расстояние АС = b.

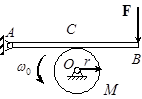
Рис.32

Задача 35. Находящаяся в вертикальной плоскости однородная пластина (рис.33) в виде прямоугольного треугольника АВС может вращаться вокруг вертикальной оси z, совпадающей со стороной АС. Масса пластины m, ее радиус инерции относительно указанной оси равен 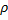. В начальный момент времени из вершины А вдоль стороны АВ начинает двигаться точечное тело 1 массы m ₁ с относительной скоростью v _r = at, где a – постоянная, а к пластине прикладывается вращающий момент M = bt, где b – постоянная. Определить угловое ускорение пластины. Угол наклона стороны АВ к горизонту равен .

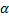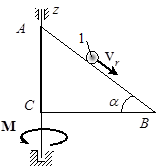
Рис.33

Задача 36. Однородный горизонтальный диск (рис.34) (радиуса r и массы m может вращаться вокруг проходящей через его центр О вертикальной оси. Вдоль радиуса ОА по направляющей может двигаться точечное тело А массы m ₀. В начальный момент времени к диску приложили постоянный вращающий момент M, а тело А начало двигаться от точки О с относительной скоростью v_r = at, где a – постоянная. Определить угловое ускорение диска.

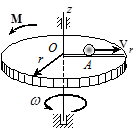
Рис.34

Задача 37. Однородный горизонтальный диск (рис.35) радиуса r и массы m вращается вокруг проходящей через его центр О вертикальной оси под действием момента M = αt, где α – постоянная. По краю диска в противоположном вращению направлении движется точечное тело А массы m ₀ с относительной скоростью v _r = at, где a – постоянная. Определить угловое ускорение диска.

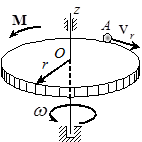
Рис.35

Задача 38. Однородный горизонтальный диск (рис.36) радиуса r и массы m вращается вокруг проходящей через его центр О вертикальной оси под действием момента M = αt, где α – постоянная. По краю диска в направлении его вращения движется точечное тело А массы m ₀ с относительной скоростью v _r = at ², где a – постоянная. Определить угловое ускорение диска.

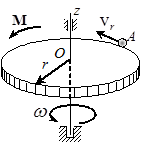
Рис.36

Пример 14. Барабан 1 веса P начинает раскручиваться из состояния покоя под действием груза 2 веса Q (рис. 37). Определить зависимость угловой скорости вращения барабана от времени. Весом нити и трением барабана об ось пренебречь, барабан считать однородным диском радиуса r.

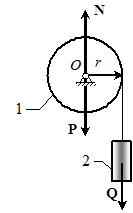
Рис.37

Решение. В качестве системы возьмем совокупность тел барабан + нить + груз (см. рис.37). Тогда внешними силами, действующими на выбранную систему, являются: силы тяжести барабана P и груза Q, а также реакция оси N. Направим ось Oz вдоль оси вращения барабана и запишем теорему об изменении момента импульса L _Z системы в проекции на эту ось

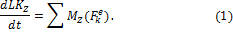
Моменты сил P и N относительно выбранной оси равны нулю, так как линии их действия проходят через ось, а момент силы Q есть M_z (Q) = – Qr. Момент импульса системы складывается из моментов импульса барабана 1 (L_{z 1}) и груза 2 (L_{z 2}) относительно данной оси: L_z = L_{z 1} + L_{z 2}, где 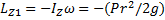, а Подставляя все эти выражения в (1), приходим к уравнению

интегрируя которое с учетом начального условия 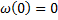, получаем искомый закон изменения угловой скорости

Date: 2015-08-15; view: 1227; Нарушение авторских прав