Особенности течения при ламинарном режиме

Ламинарный режим характерен четким выделением отдельных струек. Рассмотрим распределение касательных напряжений, давления, скоростей при ламинарном режиме (рис. 33).

Касательные напряжения. Касательное напряжение τ на произвольном удалении r от центра трубы можно записать из основного уравнения равномерного движения.

,

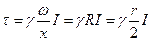где: I - гидравлический уклон, равный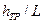

R- гидравлический радиус, равный

В соответствии с уравнением Бернулли гидравлический уклон для всех струек одинаков. Следовательно, касательные напряжения будут изменяться линейно. Максимальное значение τ у стенок трубы в прилипшем слое при 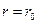, а на оси при .

Распределение давления. В этом случае действует закон статики, поэтому распределение давления происходит по гидростатическому закону. Наибольшее давление будет в точке С у нижней кромки трубы 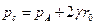причем часто разницей давления по сечению трубы можно пренебречь и считать во всех точках его равным давлению в центре тяжести сечения на оси трубы.

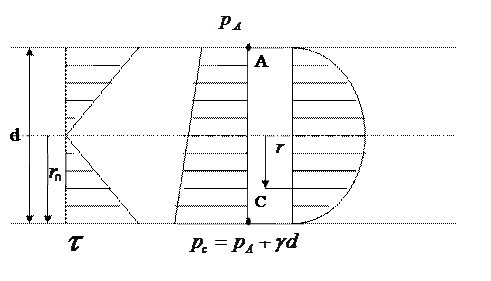
Рисунок 33 - Распределение касательных напряжений, давлений и скоростей по живому сечению при ламинарном режиме.

Распределение скоростей. Касательные напряжения при ламинарном режиме можно выразить из закона вязкого трения Ньютона:

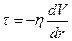
Приравняем два выражения

Из этого выражения, произведя преобразования и интегрирование, получим скорость:

Постоянную интегрирования C,определим из условий нулевой скорости на стенках трубы (U=0 при r=0),откуда

Окончательно закон распределения скоростей имеет вид

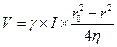; при r=0;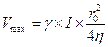

Эпюра скоростей в живом сечении представляет собой парабалоид вращения. Скорость изменяется от нуля в прилипшем слое у стенок трубы до V_max на оси.

Расход и средняя скорость. Элементарный расход в живом кольцевом сечении толщиной dr и удаленном от центра на расстояние r можно выразить по формуле:

.

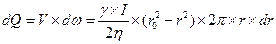Проинтегрировав это выражение от 0 до , получим расход потока жидкости:

.

Среднюю скорость определим из уравнения неразрывности , где 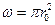, тогда:

.

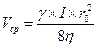Сопоставив выражения для расчета максимальной скорости V_max и средней скорости отметим, что они связаны соотношением: , с учетом этого соотношения, закон распределения скоростей можно записать так:

.

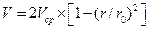Потери энергии (напора) и коэффициент Дарси. Формулу для определения потерь энергии на трение в круглой трубе можно получить, преобразовав формулу для расчета средней скорости, выразив в ней гидравлический уклон как , тогда

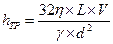(формула Пуазейля)

В общем случае потери энергии на трение выражается формулой Дарси-Вейсбаха:

h_ТР= .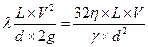

С учетом известных соотношений: , получим значение коэффициента Дарси для ламинарного режима:

.

Анализируя формулу, можно сделать вывод о линейной зависимости коэффициента Дарси от числа Рейнольдса Re, а также о такой же зависимости потерь на трение (по длине) 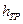от средней скорости V.

Date: 2015-08-15; view: 489; Нарушение авторских прав