Перейдем теперь к удару упругих тел

Ударный процесс таких тел происходит гораздо сложнее. Под действием ударной силы деформация их сначала увеличивается, увеличивается до тех пор пока скорости тел не уравняются. А затем, за счет упругости материала, начнется восстановление формы. Скорости тел начнут изменяться, изменяться до тех пор пока тела не отделятся друг от друга.

Разделим процесс удара на две стадии: от начала удара до того момента, когда скорости их уравняются и будут равными u; и от этого момента до конца удара, когда тела разойдутся со скоростям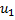и и .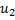

Для каждой стадии получим по два уравнения:

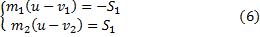
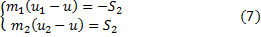
где S ₁ и S ₂ – величины импульсов взаимных реакций тел для первой и второй стадий.

Уравнения (6) аналогичны уравнениям (2). Решая их, получим

В уравнениях (7) три неизвестные величины (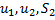). Не хватает одного уравнения, которое опять должно характеризовать физические свойства этих тел.

Положим отношение импульсов S₂/S₁=k. Это и будет дополнительное третье уравнение.

Опыт показывает, что величину k можно считать зависящей только от упругих свойств этих тел. (Правда, более точные эксперименты показывают, что есть некоторые зависимости и от их формы). Определяется этот коэффициент экспериментально для каждых конкретных тел. Называется он коэффициентом восстановления скорости. Величина его 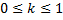. У пластичных тел k = 0, у абсолютно упругих тел k = 1.

Решая, теперь, уравнения (7) и (6), получим скорости тел после окончания удара.

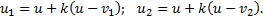(8)

Скорости имеют положительный знак, если они совпадают с положительным направлением оси, выбранной нами, и отрицательный – в противном случае.

Проанализируем полученные выражения для двух шаров различных масс.

1) m₁=m₂ ⇒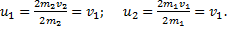

Шары равной массы «обмениваются» скоростями.

2) m₁>m₂, v₂=0,

u₁<v₁, следовательно, первый шар продолжает двигаться в том же направлении, как и до удара, но с меньшей скоростью;

u₂>u₁, следовательно, скорость второго шара после удара больше, чем скорость первого после удара.

3) m₁<m₂, v₂=0,

u₁<0, следовательно, направление движения первого шара при ударе изменяется – шар отскакивает обратно.

u₂<v₁, следовательно, второй шар в ту же сторону, в которую двигался первый шар до удара, но с меньшей скоростью.

4) m₂>>m₁ (например, столкновение шара со стенкой)

u₁=-v₁, 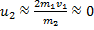, следовательно, получившее удар большое тело останется в покое, а ударившее малое тело отскочит с первоначальной скоростью в противоположную сторону.

Можно найти, как и при ударе пластичных тел, потерю кинетической энергии при ударе упругих тел. Она получится такой

Заметим, что при ударе абсолютно упругих тел (k = 1) кинетическая энергия не изменяется, не «теряется» (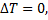 T₁=T₂).

Пример 1. Металлический шарик падает с высоты h ₁ на горизонтальную массивную плиту. После удара он подскакивает на высоту h ₂ (рис.3).

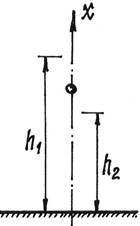
Рис.3

В начале удара о плиту проекция скорости шарика на ось х 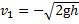а скорость неподвижной плиты 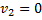. Считая, что масса плиты 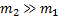, много больше массы шарика, можно положить u = 0 и u ₂ = 0. Тогда по (8) 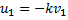. (Теперь, кстати, понятно почему коэффициент k называется коэффициентом восстановления скорости.)

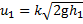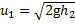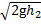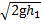Итак, скорость шарика в конце удара и направлена вверх (u ₁ > 0). Шарик подскакивает на высоту h ₂, связанную со скоростью формулой Значит, =k и 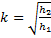По последней формуле, кстати, и определяется коэффициент восстановления k для материалов, из которых сделаны шарик и плита.

Пример 2. Шар массой m₁=2 кг движется со скоростью v₁=3 м/с и нагоняет шар массой m₂=8 кг, движущийся со скоростью v₂=1 м/с (рис.4). Считая удар центральным и абсолютно упругим, найти скорости u₁ и u₂ шаров после удара.

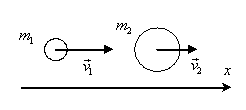
Рис.4

Решение. В случае абсолютно упругого удара выполняются законы сохранения импульса и энергии:

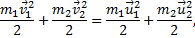
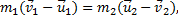
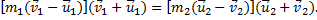
Отсюда следует, что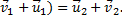

Умножив это выражение на m₂ и вычтя результат из 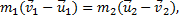а затем, умножив это выражение на m₁ и сложив результат с 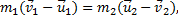получим скорости шаров после абсолютно упругого удара

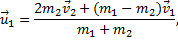
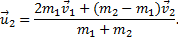
Спроецировав скорости на ось х и подставив данные задачи, получим

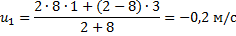
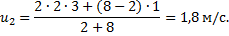
Знак «минус» в первом выражении означает, что в результате абсолютно упругого удара первый шар начал двигаться в обратном направлении. Второй шар продолжил движение в прежнем направлении с большей скоростью.

Пример 3. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нем (рис.5). Масса пули в 1000 раз меньше массы шара. Расстояние от центра шара до точки подвеса стержня l= 1 м. Найти скорость v пули, если известно, что стержень с шаром отклонился от удара пули на угол α=10°.

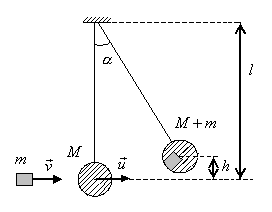
Рис.5

Решение. Для решения задачи необходимо использовать законы сохранения. Запишем закон сохранения импульса для системы «шар-пуля», полагая, что их взаимодействие подпадает под описание так называемого неупругого удара, т.е. взаимодействия, в результате которого два тела движутся как единое целое:

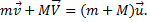
Учтем, что шар покоился и движение пули, а затем шара с пулей внутри происходило в одну сторону, получим уравнение в проекциях на горизонтальную ось в виде: mv=(m+M)u.

Запишем закон сохранения энергии

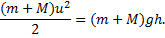
Поскольку h=l=lcos𝛼=l(1-cos𝛼), то , и, тогда

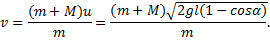
Учитывая, что M=1000m, получим

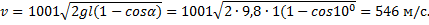
Пример 4. Шар массой m, двигаясь со скоростью v, упруго ударяется о стенку под углом α. Определить импульс силы F∆t, полученный стенкой.

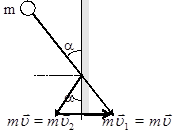
Рис.6

Решение. Изменение импульса шара численно равно импульсу силы, который получит стенка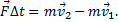

Из рис.6 F∆t=2mv∙sinα.

Пример 5. Пуля (рис.7) веса Р ₁, летящая горизонтально со скоростью u, попадает в закрепленный на неподвижной тележке ящик с песком веса Р ₂. С какой скоростью будет двигаться тележка после удара, если трением колес о Землю можно пренебречь?

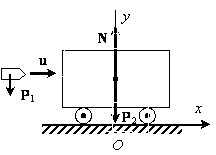
Рис.7

Решение. Будем рассматривать пулю и тележку с песком как одну систему (рис. 7). На нее действуют внешние силы: вес пули Р ₁, вес тележки Р ₂, а также силы реакции колес. Поскольку трение отсутствует, то эти последние направлены вертикально вверх и их можно заменить равнодействующей N. Для решения задачи воспользуемся теоремой об изменении количества движения системы в интегральной форме. В проекции на ось Ox (см. рис. 77) тогда имеем

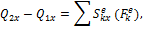
где 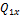– количество движения системы до удара, а 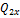– после удара. Поскольку все внешние силы вертикальны, то правая часть этого уравнения равна нулю и поэтому .

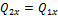Так как до удара тележка покоилась, то . После удара система движется как единое целое с искомой скоростью v и, следовательно, Q _{2 x} =(P ₁+ P ₂)v/ g. Приравнивая эти выражения, находим искомую скорость: v= P ₁ u /(P ₁+ P ₂).

Пример 6. Тело массой m₁ = 5 кг ударяется о неподвижное тело массой m₂ = 2,5 кг. Кинетическая энергия системы двух тел непосредственно после удара стала W _к = 5 Дж. Считая удар центральным и неупругим, найти кинетическую энергию W _к1 первого тела до удара.

Date: 2015-08-15; view: 837; Нарушение авторских прав