Максвелл ввел понятие полного тока,равного сумме токов проводимости (а также конвекционных токов) и смещения.Плотность полного тока 5 page

Магнитострикция — это возникновение деформации в ферромагнетиках под дейст­вием магнитного поля. Поместив ферромагнитный стержень (например, из никеля или железа) в быстропеременное магнитное поле, возбуждают его механические колебания, амплитуда которых максимальна в случае резонанса.

Ультразвуки широко используются в технике, например для направленной подводкой сигнализации, обнаружения подводных предметов и определения глубин (гидролока­тор, эхолот). Например, в эхолоте от пьезокварцевого генератора, укрепленного на судне, посылаются направленные ультразвуковые сигналы, которые, достигнув дна, отражаются от него и возвращаются обратно. Зная скорость их распространения в воде и определяя время прохождения (от подачи до возвращения) ультразвукового сигнала, можно вычислить глубину. Прием эха также производится с помощью пьезокварца. Звуковые колебания, дойдя да пьезокварца, вызывают в нем упругие колебания, в результате чего на противоположных поверхностях кварца возникают электрические заряды, которые измеряются.

Если пропускать ультразвуковой сигнал через исследуемую деталь, то можно обнаружить в ней дефекты по характерному рассеянию пучка и по появлению ультра­звуковой тени. На этом принципе создана целая отрасль техники — ультразвуковая дефектоскопия, начало которой положено С. Я. Соколовым (1897—1957). Применение ультразвука легло также в основу новой области акустики — акустоэлектроники, по­зволяющей на ее основе разрабатывать приборы для обработки сигнальной инфор­мации в микрорадиоэлектронике.

Ультразвук применяют для воздействия на различные процессы (кристаллизацию, диффузию, тепло- и массообмен в металлургии и т. д.) и биологические объекты (повышение интенсивности процессов обмена и т. д.), для изучения физических свойств веществ (поглощения, структуры вещества и т. д.). Ультразвук используется также для механической обработки очень твердых и очень хрупких тел, в медицине (диагностика, ультразвуковая хирургия, микромассаж тканей) и т. д.

Задачи

19.1. Плоская гармоническая волна распространяется вдоль прямой, совпадающей с положи­тельным направлением оси х в среде, не поглощающей энергию, со скоростью v =12 м/с. Две точки, находящиеся на этой прямой на расстояниях x ₁ = 7 м и x ₂=12 м от источника колебаний, колеблются с разностью фаз D j = ⁵/₆ p. Амплитуда волны А = 6 см. Опреде­лить: 1) длину волны l; 2) уравнение волны; 3) смещение x ₂ второй точки в момент времени t = 3 с. [1) 12 см; 2) x (х, t) = 0,06 cos (2 pt – pх /6); 3) 6 см]

19.2. Два динамика расположены на расстоянии 2 м друг от друга и воспроизводят один и тот же музыкальный тон на частоте 1000 Гц. Приемник находится на расстоянии 4 м от центра динамиков. Принимая скорость звука 340 м/с, определить, на какое расстояние от центра­льной линии параллельно динамикам надо отодвинуть приемник, чтобы он зафиксировал первый интерференционный минимум. [0,34 м]

19.3. Для определения скорости звука в воздухе методом акустического резонанса исполь­зуется труба с поршнем и звуковой мембраной, закрывающей один из ее торцов. Расстоя­ние между соседними положениями поршня, при котором наблюдается резонанс на частоте 1700 Гц, составляет 10 см. Определить скорость звука в воздухе. [340 м/с]

19.4. Средняя квадратичная скорость молекул двухатомного газа при некоторых условиях составляет 461 м/с. Определить скорость распространения звука при тех же условиях. [315 м/с]

19.5. Поезд проходит со скоростью 54 км/ч мимо неподвижного приемника и подает звуковой сигнал. Приемник воспринимает скачок частоты D n = 54 Гц. Принимая скорость звука равной 340 м/с, определить частоту тона звукового сигнала гудка поезда. [611 Гц]

Глава 20 Электромагнитные волны

§ 161. Экспериментальное получение электромагнитных волн

Существование электромагнитных волн — переменного электромагнитного поля, распространяющегося в пространстве с конечной скоростью, — вытекает из уравнений Максвелла (см. § 139). Уравнения Максвелла сформулированы в 1865 г. на основе обобщения эмпирических законов электрических и магнитных явлений. Как уже указы­валось, решающую роль для утверждения максвелловской теории сыграли опыты Герца (1888), доказавшие, что электрические и магнитные поля действительно рас­пространяются в виде воли, поведение которых полностью описывается уравнениями Максвелла.

Источником электромагнитных волн в действительности может быть любой элект­рический колебательный контур ила проводник, по которому течет переменный элект­рический ток, таккак для возбуждения электромагнитных волн необходимо создать в пространстве переменное электрическое поле (ток смещения) или соответственно переменное магнитное поле. Однако излучающая способность источника определяется его формой, размерами и частотой колебаний. Чтобы излучение играло заметную роль, необходимо увеличить объем пространства, в котором переменное электромаг­нитное поле создается. Поэтому для получения электромагнитных волн непригодны закрытые колебательные контуры, так как в них электрическое поле сосредоточено между обкладками конденсатора, а магнитное — внутри катушки индуктивности.

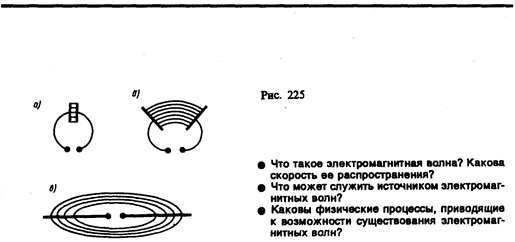
Герц в своих опытах, уменьшая число витков катушки и площадь пластин конден­сатора, а также раздвигая их (рис. 225, а, б), совершил переход от закрытого колеба­тельного контурак открытому колебательному контуру (вибратору Герца), представ­ляющему собой два стрежня, разделенных искровым промежутком (рис. 225, в). Если в закрытом колебательном контуре переменное электрическое поле сосредоточено внутри конденсатора (рис. 225, а), то в открытом оно заполняет окружающее контур пространство (рис. 255, в), что существенно повышает интенсивность электромагнит­ного излучения. Колебания в такой системе поддерживаются за счет источника э.д.с., подключенного к обкладкам конденсатора, а искровой промежуток применяется для того, чтобы увеличить разность потенциалов, до которой первоначально заряжаются обкладки.

Для возбуждения электромагнитных воли вибратор Герца В подключался к индуктору И (рис. 226). Когда напряжение на искровом промежутке достигало пробивного значения, возникала искра, закорачивающая обе половины вибратора, и в нем воз­никали свободные затухающие колебания. При исчезновении искры контур размыкался и колебания прекращались. Затем индуктор снова заряжал конденсатор, возникала искра и в контуре опять наблюдались колебания и т. д. Для регистрации электромаг­нитных воли Герц пользовался вторым вибратором, называемым резонатором Р, имеющим такую же частоту собственных колебаний, что и излучающий вибратор, т. е. настроенным в резонанс с вибратором. Когда электромагнитные волны достигали резонатора, то в его зазоре проскакивала электрическая искра.

С помощью описанного вибратора Герц экспериментировал с электромагнитными волнами, длина волны которых составляла примерно 3 м. П. Н. Лебедев, применяя миниатюрный вибратор из тонких платиновых стерженьков, получил миллиметровые электромагнитные волны с l = 6 – 4 мм. Дальнейшее развитие методики эксперимен­та в этом направлении позволило в 1923 г. российскому физику А. А. Глаголе­вой-Аркадьевой (1884—1945) сконструировать массовый излучатель, в котором корот­кие электромагнитные волны, возбуждаемые колебаниями электрических зарядов в атомах и молекулах, генерировались с помощью искр, проскакиваемых между металлическими опилками, взвешенными в масле. Так были получены волны с l от 50 мм до 80 мкм. Тем самым было доказано существование волн, перекрывающих интервал между радиоволнами и инфракрасным излучением.

Недостатком вибраторов Герца и Лебедева и массового излучателя Глаголе­вой-Аркадьевой являлось то, что свободные колебания в них быстро затухали и об­ладали малой мощностью. Для получения незатухающих колебаний необходимо со­здать автоколебательную систему (см. § 146), которая обеспечивала бы подачу энергии с частотой, равной частоте собственных колебаний контура. Поэтому в 20-х годах нашего столетия перешли к генерированию электромагнитных волн с помощью элект­ронных ламп. Ламповые генераторы позволяют получать колебания заданной (прак­тически любой) мощности и синусоидальной формы.

Электромагнитные волны, обладая широким диапазоном частот (или длин волн l = c / n, где с — скорость электромагнитных волн в вакууме), отличаются друг от друга по способам их генерации и регистрации, а также по своим свойствам. Поэтому электромагнитные волны делятся на несколько видов: радиоволны, световые волны, рентгеновское и g -излучения (табл.5). Следует отметить, что границы между различ­ными видами электромагнитных волн довольно условны.

Таблица 5

Продолжение табл. 5

§ 162. Дифференциальное уравнение электромагнитной волны

Как уже указывалось (см. § 161), одним из важнейших следствий уравнений Максвелла (см. § 139) является существование электромагнитных воли. Можно показать, что для однородной и изотропной среды вдали от зарядов и токов, создающих электромагнитное поле, из уравнений Максвелла следует, что векторы напряженностей Е и Н переменного электромагнитного поля удовлетворяют волновому уравнению типа (154.9):

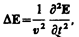(162.1)

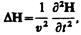(162.2)

где 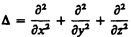— оператор Лапласа, v — фазовая скорость.

Всякая функция, удовлетворяющая уравнениям (162.1) и (162.2), описывает некото­рую волну. Следовательно, электромагнитные поля действительно могут существовать в виде электромагнитных волн. Фазовая скорость электромагнитных воли определяет­ся выражением

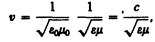(162.3)

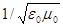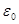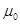где с = , и — соответственно электрическая и магнитная постоянные, e и m — соответственно электрическая и магнитная проницаемости среды.

В вакууме (при e =1 и m =l) скорость распространения электромагнитных волн совпадает со скоростью с. Так как em > 1, то скорость распространения электромагнит­ных воли в веществе всегда меньше, чем в вакууме.

При вычислении скорости распространения электромагнитного поля по формуле (162.3) получается результат, достаточно хорошо совпадающий с экспериментальными данными, если учитывать зависимость e и m от частоты. Совпадение же размерного коэффициента в (162.3) со скоростью распространения света в вакууме указывает на глубокую связь между электромагнитными и оптическими явлениями, позволившую Максвеллу создать электромагнитную теорию света, согласно которой свет представ­ляет собой электромагнитные волны.

Следствием теории Максвелла является поперечность электромагнитных волн: век­торы Е и Н напряженностей электрического и магнитного полей волны взаимно перпендикулярны (на рис. 227 показана моментальная «фотография» плоской электро­магнитной волны) и лежат в плоскости, перпендикулярной вектору v скорости рас­пространения волны, причем векторы Е, Н и v образуют правовинтовую систему. Из уравнений Максвелла следует также, что в электромагнитной волне векторы Е и Н все­гда колеблются в одинаковых фазах (см. рис. 227), причем мгновенные значения Е и Н в любой точке связаны соотношением

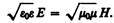(162.4)

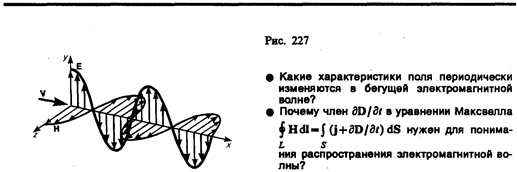
Следовательно, Е и Н одновременно достигают максимума, одновременно обраща­ются в нуль и т. д. От уравнений (162.1) и (162.2) можно перейти к уравнениям

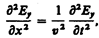(162.5)

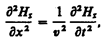(162.6)

где соответственно индексы у и z при Е и Н подчеркивают лишь то, что векторы Е и Н направлены вдоль взаимно перпендикулярных осей y и z.

Уравнениям (162.5) и (162.6) удовлетворяют, в частности, плоские монохроматические электромагнитные волны (электромагнитные волны одной строго определенной частоты), описываемые уравнениями

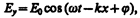(162.7)

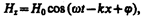(162.8)

где E ₀ и Н ₀ — соответственно амплитуды напряженностей электрического и магнит­ного полей волны, w — круговая частота волны, k=w/v — волновое число, j — на­чальные фазы колебаний в точках с координатой х= 0. В уравнениях (162.7) и (162.8) j одинаково, так как колебания электрического и магнитного векторов в электромаг­нитной волне происходят в одинаковых фазах.

§ 163. Энергия электромагнитных волн. Импульс электромагнитного поля

Возможность обнаружения электромагнитных воли указывает на то, что они переносят энергию. Объемная плотность w энергии электромагнитной волны складывается из объемных плотностей w _эл (см. (95.8)) и w _м, (см. (130.3)) электрического и магнитного полей:

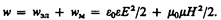
Учитывая выражение (162.4), получим, что плотности энергии электрического и маг­нитного полей в каждый момент времени одинаковы, т. е. w _эл = w _м. Поэтому

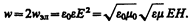
Умножив плотность энергии w на скорость v распространения волны в среде (см. (162.3)), получим модуль плотности потока энергии:

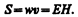
Tax как векторы Е и Н взаимно перпендикулярны и образуют с направлением распространения волны правовинтовую систему, то направление вектора [ ЕН ] совпада­ет с направлением переноса энергии, а модуль этого вектора равен ЕН. Вектор плотности потока электромагнитной энергии называется вектором Умова — Пойнтинга:

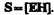
Вектор S направлен в сторону распространения электромагнитной волны, а его модуль равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны.

Если электромагнитные волны поглощаются или отражаются телами (эти явления подтверждены опытами Г. Герца), то из теории Максвелла следует, что электромаг­нитные волны должны оказывать на тела давление. Давление электромагнитных волн объясняется тем, что под действием электрического поля волны заряженные частицы вещества начинают упорядоченно двигаться и подвергаются со стороны магнитного поля волны действию сил Лоренца. Однако значение этого давления ничтожно мало. Можно оценить, что при средней мощности солнечного излучения, приходящего на Землю, давление для абсолютно поглощающей поверхности составляет примерно 5 мкПа. В исключительно тонких экспериментах, ставших классическими, П. Н. Лебе­дев в 1899 г. доказал существование светового давления на твердые тела, а в 1910 г. — на газы. Опыты Лебедева имели огромное значение для утверждения выводов теории Максвелла о том, что свет представляет собой электромагнитные волны.

Существование давления электромагнитных воли приводит к выводу о том, что электромагнитному полю присущ механический импульс. Импульс электрома­гнитного поля

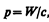
где W — энергия электромагнитного поля. Выражая импульс как р=тс (поле в ваку­уме распространяется со скоростью с), получим р=тс= W/c, откуда

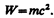(163.1)

Это соотношение между массой и энергией электромагнитного поля является универ­сальным законом природы (см. также § 40). Согласно специальной теории относитель­ности, выражение (163.1) имеет общее значение и справедливо для любых тел независи­мо от их внутреннего строения.

Таким образом, рассмотренные свойства электромагнитных волн, определяемые теорией Максвелла, полностью подтверждаются опытами Герца, Лебедева и выводами специальной теории относительности, сыгравшими решающую роль для подтвержде­ния и быстрого признания этой теории.

§ 164. Излучение диполя. Применение электромагнитных волн

Простейшим излучателем электромагнитных волн является электрический диполь, электрический момент которого изменяется во времени по гармоническому закону

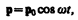
где р ₀ — амплитуда вектора р. Примером подобного диполя может служить система, состоящая из покоящегося положительного заряда + Q и отрицательного заряда –Q, гармонически колеблющегося вдоль направления р с частотой w.

Задача об излучении диполя имеет в теории излучающих систем важное значение, так как всякую реальную излучающую систему (например, антенну) можно рассчиты­вать рассматривая излучение диполя. Кроме того, многие вопросы взаимодействия излучения с веществом можно объяснить на основе классической теории, рассматривая атомы как системы зарядов, в которых электроны совершают гармонические колеба­ния около их положений равновесия.

Характер электромагнитного поля диполя зависит от выбора рассматриваемой точки. Особый интерес представляет так называемая волновая зона диполя — точки пространства, отстоящие от диполя на расстояниях r, значительно превышающих длину волны (r >> l), — так как в ней картина электромагнитного поля диполя сильно упрощается. Это связано с тем, что в волновой зоне диполя практически остаются только «отпочковавшиеся» от диполя, свободно распространяющиеся поля, в то время как поля, колеблющиеся вместе с диполем и имеющие более сложную структуру, сосредоточены в области расстояний r < l.

Если волна распространяется в однородной изотропной среде, то время прохожде­ния волны до точек, удаленных от диполя на расстояние r, одинаково. Поэтому во всех точках сферы, центр которой совпадает с диполем, фаза колебаний одинакова, т. е. в волновой зоне волновой фронт будет сферическим и, следовательно, волна, излуча­емая диполем, есть сферическая волна.

В каждой точке векторы Е и Н колеблются по закону cos(wt—kr), амплитуды этих векторов пропорциональны (1/ r) sin q (для вакуума), т. е. зависят от расстояния r до излучателя и угла q между направлением радиуса-вектора и осью диполя. Отсюда следует, что интенсивность излучения диполя в волновой зоне

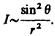(164.1)

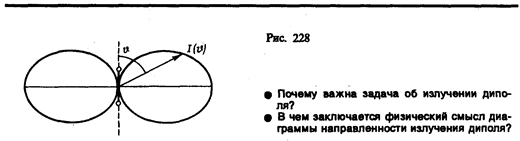
Зависимость (164.1) I от q при заданном значении r, приводимая в полярных коор­динатах (рис. 228), называется диаграммой направленности излучения диполя. Как видно из выражения (164.1) и приведенной диаграммы, диполь сильнее всего излучает в на­правлениях, перпендикулярных его оси (q = p /2). Вдоль своей оси (q =0 и q = p) диполь не излучает вообще. Диаграмма направленности излучения диполя позволяет фор­мировать излучение с определенными характеристиками и используется при констру­ировании антенн.

Впервые электромагнитные волны были использованы через семь лет после опытов Герца. 7 мая 1895 г. преподаватель физики офицерских минных классов А. С. Попов (1859—1906) на заседании Русского физико-химического общества продемонстрировал первый в мире радиоприемник, открывший возможность практического использования электромагнитных волн для беспроволочной связи, преобразившей жизнь человечест­ва. Первая переданная в мире радиограмма содержала лишь два слова: «Генрих Герц». Изобретение радио Поповым сыграло огромную роль для распространения и развития теории Максвелла.

Электромагнитные волны сантиметрового и миллиметрового диапазонов, встречая на своем пути преграды, отражаются от них. Это явление лежит в основе радиолока­ции — обнаружения предметов (например, самолетов, кораблей и т. д.) на больших расстояниях и точного определения их положения. Помимо этого, методы радиолока­ции используются для наблюдения прохождения и образования облаков, движения метеоритов в верхних слоях атмосферы и т. д.

Для электромагнитных волн характерно явление дифракции — огибания волнами различных препятствий. Именно благодаря дифракции радиоволн возможна устой­чивая радиосвязь между удаленными пунктами, разделенными между собой выпук­лостью Земли. Длинные волны (сотни и тысячи метров) применяются в фототеле­графии, короткие волны (несколько метров и меньше) применяются в телевидении для передачи изображений на небольшие расстояния (немногим больше пределов прямой видимости). Электромагнитные волны используются также в радиогеодезии для очень точного определения расстояний с помощью радиосигналов, в радиоастрономии для исследования радиоизлучения небесных тел и т. д. Полное описание применения электромагнитных волн дать практически невозможно, так как нет областей науки и техники, где бы они не использовались.

Задачи

20.1. Электромагнитная волна с частотой 4 МГц переходит из немагнитной среды с диэлект­рической проницаемостью e =3 в вакуум. Определить приращение ее длины волны. [31,7 м]

20.2. Два параллельных провода, одни концы которых изолированы, а другие индуктивно соединены с генератором электромагнитных колебаний, погружены в спирт. При соответ­ствующем подборе частоты колебаний в системе возникают стоячие волны. Расстояние между двумя узлами стоячих волн на проводах равно 0,5 м. Принимая диэлектрическую проницаемость спирта e = 26, а его магнитную проницаемость m =1, определить частоту колебаний генератора. [58,8 МГц]

20.3. В вакууме вдоль оси х распространяется плоская электромагнитная волна. Амплитуда напряженности электрического поля волны составляет 18,8 В/м. Определить интенсив­ность волны, т.е. среднюю энергию, приходящуюся за единицу времени на единицу площади, расположенной перпендикулярно направлению распространения волны. [0,47 Вт/м²]

5 ОПТИКА. КВАНТОВАЯ ПРИРОДА ИЗЛУЧЕНИЯ

Глава 21 Элементы геометрической и электронной оптики

§ 165. Основные законы оптики. Полное отражение

Еще до установления природы света были известны следующие основные законы оптики: закон прямолинейного распространения света в оптически однородной среде; закон независимости световых пучков (справедлив только в линейной оптике); закон отражения света; закон преломления света.

Закон прямолинейного распространения света: свет в оптически однородной среде распространяется прямолинейно.

Доказательством этого закона является наличие тени с резкими границами от непрозрачных предметов при освещении их точечными источниками света (источники, размеры которых значительно меньше освещаемого предмета и расстояния до него). Тщательные эксперименты показали, однако, что этот закон нарушается, если свет проходит сквозь очень малые отверстия, причем отклонение от прямолинейности распространения тем больше, чем меньше отверстия.

Закон независимости световых пучков: эффект, производимый отдельным пучком, не зависит от того, действуют ли одновременно остальные пучки или они устранены. Разбивая световой поток на отдельные световые пучки (например, с помощью диа­фрагм), можно показать, что действие выделенных световых пучков независимо.

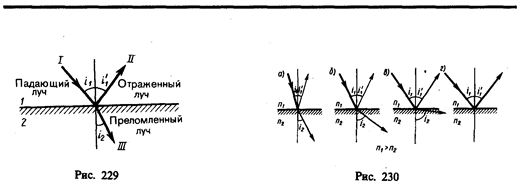
Если свет падает на границу раздела двух сред (двух прозрачных веществ), то падающий луч I (рис. 229) разделяется на два — отраженный II и преломленный III, направления которых задаются законами отражения и преломления.

Закон отражения: отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела двух сред в точке падения; угол i '₁ отражения равен углу i ₁ падения:

Закон преломления: луч падающий, луч преломленный и перпендикуляр, проведен­ный к границе раздела в точке падения, лежат в одной плоскости; отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред:

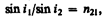(165.1)

где n ₂₁ — относительный показатель преломления второй среды относительно первой. Индексы в обозначениях углов i ₁, i '₁, i ₂ указывают, в какой среде (первой или второй) идет луч.

Относительный показатель преломления двух сред равен отношению их абсолют­ных показателей преломления:

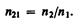(165.2)

Абсолютным показателем преломления среды называется величина n, равная от­ношению скорости c электромагнитных волн в вакууме к их фазовой скорости v в среде:

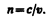(165.3)

Сравнение с формулой (162.3) дает, что 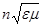, где e и m — соответственно электри­ческая и магнитная проницаемости среды. Учитывая (165.2), закон преломления (165.1) можно записать в виде

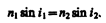(165.4)

Из симметрии выражения (165.4) вытекает обратимость световых лучей. Если обратить луч III (рис.229), заставив его падать на границу раздела под углом i ₂, то преломлен­ный луч в первой среде будет распространяться под углом i ₁, т. е. пойдет в обратном направлении вдоль луча I.

Если свет распространяется из среды с большим показателем преломления n ₁ (оп­тически более плотной) в среду с меньшим показателем преломления n ₂ (оптически менее плотную) (n ₁> n ₂), например из стекла в воду, то, согласно (165.4),

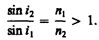
Отсюда следует, что преломленный луч удаляется от нормали и угол преломления i ₂ больше,чем угол падения i ₁ (рис. 230, а). С увеличением угла падения увеличивается угол преломления (рис. 230, б, в) до тех пор, пока при некотором угле падения (i ₁= i _пр) угол преломления не окажется равным p /2. Угол i _пр называется предельным углом. При углах падения i ₁> i _пр весь падающий свет полностью отражается (рис. 230, г).

По мере приближения угла падения к предельному интенсивность преломленного луча уменьшается, а отраженного — растет (рис. 230, а—в). Если i ₁= i _пр, то интенсив­ность преломленного луча обращается в нуль, а интенсивность отраженного равна интенсивности падающего (рис. 230, г). Таким образом, при углах падения в пределах от i _пр до p /2 луч не преломляется, а полностью отражается в первую среду, причем интенсивности отраженного и падающего лучей одинаковы. Это явление называется полным отражением.

Предельный угол i _пр определим из формулы (165.4) при подстановке в нее i ₂= p /2.

Тогда

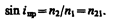(165.5)

Уравнение (165.5) удовлетворяет значениям угла i _пр при n ₂ £ n ₁. Следовательно, явление полного отражения имеет место только при падении света из среды оптически более плотной в среду оптически менее плотную.

Date: 2015-08-15; view: 465; Нарушение авторских прав