Типовые задачи

Задача № 1.

Найти производную функции 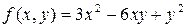в точке 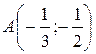в направлении , составляющем угол a положительным направлением оси Ох.

В каком направлении эта производная имеет:

а) наибольшее значение

б) наименьшее значение

в) значение, равное нулю?

Решение.

По условию задачи .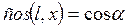

Тогда .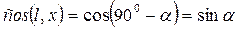

.

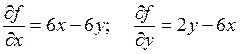Подстановка в формулу:

дает

.

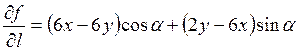В точке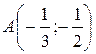

.

Теперь найдем те значения a, при которых имеет значения а) наибольшее, б) наименьшее, в) значение, равное нулю.

Обозначим и найдем экстремум этой функции.

.

Считая, что 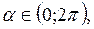получим:

;

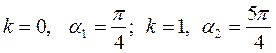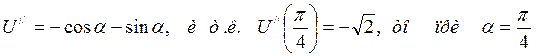
функция достигает максимума.

При 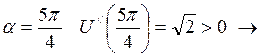функция достигает минимума.

При 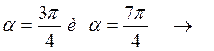функция U =0.

Ответ: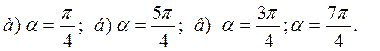

Задача № 2.

Найти производную скалярного поля U=xyz в точке М₀ (1,-1,1) по направлению от т. М₀ к точке М₁ (2,3,1).

Решение.

Найдем 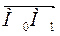и его направляющие косинусы

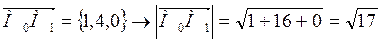
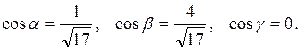
Найдем частные производные функции U=xyz в точке М₀ (1,-1,1).

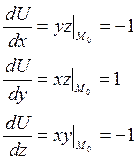
Полученные значения частных производных и направляющих косинусов подставим в формулу:

.

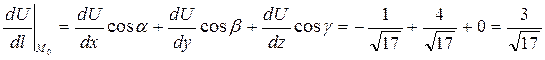Тот факт, что , означает, что скалярное поле в точке М₀ в данном направлении возрастает.

«Градиент»

Градиентом функции U (x,y,z) в точке M (x,y,z) называется вектор, проекциями которого на оси координат служат значения частных производных этой функции в данной точке, т.е.

.

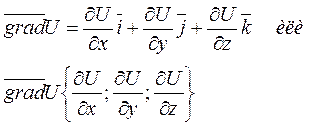
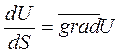Направление 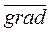есть направление наискорейшего возрастания функции. В противоположном направлении функция быстрее всего убывает.

Типовые примеры

№ 1. С какой наибольшей скоростью может возрастать функция

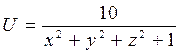при переходе точки M (x,y,z) через точку M₀ (-1,2,-2)?

В каком направлении должна двигаться точка M при переходе через точку M₁ (2,0,1), чтобы функция U(M) убывала с наибольшей скоростью?

Решение.

Наибольшая по абсолютной величине скорость изменения функции U(M) при переходе через т. Р численно равна модулю градиента функции в точке Р. При этом функция будет возрастать или убывать с наибольшей скоростью, смотря по тому, будет ли точка M при переходе через точку Р двигаться по направлению градиента функции в точке Р или по прямо противоположному направлению.

Итак, находим градиент функции U(M):

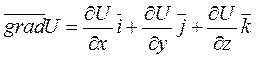
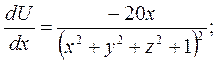
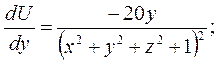
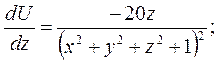
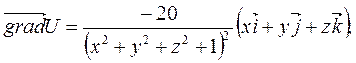
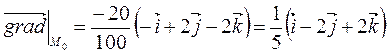
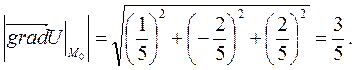
Итак, наибольшая скорость возрастания функции U(M) при переходе точки М через точку М₀ равна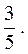

Итак, чтобы функция убывала с наибольшей скоростью при переходе через точку М, точка М должна двигаться в направлении, противоположном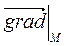

№ 2. Найти точки, в которых функция стационарна, т.е. точки, в которых производная по любому направлению равна нулю.

Решение.

Чтобы в некоторой точке Р производная функция по любому направлению была равна нулю, необходимо и достаточно, чтобы в этой точке все частные производные первого порядка функции одновременно обращались в нуль.

;

;

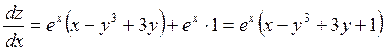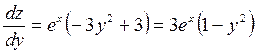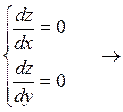
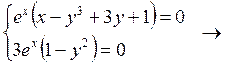
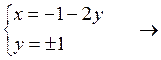
М₁ (1,-1), М₂ (-3,1).

Ответ: функция z стационарна в точках М₁ (1,-1), М₂ (-3,1).

Date: 2015-08-07; view: 2505; Нарушение авторских прав