
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Линейные блочные коды
|
|
Блочный код определяется, как набор возможных кодов, который получается из последовательности бит, составляющих сообщение. Например, если мы имеем К бит, то имеется 2К возможных сообщений и такое же число кодов, которые могут быть получены из этих сообщений. Набор этих кодов представляет собой блочный код. Линейные коды получаются в результате перемножения сообщения М на порождающую матрицу G[IA]. Каждой порождающей матрице ставится в соответствие матрица проверки четности (n-k)*n. Эта матрица позволяет исправлять ошибки в полученных сообщениях путем вычисления синдрома. Матрица проверки четности находится из матрицы идентичности i и транспонированной матрицы А. G[IA] ==> H[ATI].
| I | A | AT |
Если 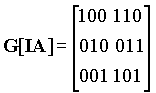 , то H[ATI] =
, то H[ATI] = 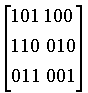
Синдром полученного сообщения равен
S = [полученное сообщение]. [матрица проверки четности].
Если синдром содержит нули, ошибок нет, в противном случае сообщение доставлено с ошибкой. Если сообщение М соответствует М=2k, а k =3 высота матрицы, то можно записать восемь кодов:
| Сообщения | Кодовые вектора | Вычисленные как |
| M1 = 000 | V1 = 000000 | M1.G |
| M2 = 001 | V2 = 001101 | M2.G |
| M3 = 010 | V3 = 010011 | M3. G |
| M4 = 100 | V4 = 100110 | M4. G |
| M5 = 011 | V5 = 011110 | M5.G |
| M6 = 101 | V6 = 101011 | M6 .G |
| M7 = 110 | V7 = 110101 | M7 .G |
| M8 = 111 | V8 = 111000 | M8 .G |
Кодовые векторы для этих сообщений приведены во второй колонке. На основе этой информации генерируется таблица 1, которая называется стандартным массивом. Стандартный массив использует кодовые слова и добавляет к ним биты ошибок, чтобы получить неверные кодовые слова.
Таблица1.Стандартный массив для кодов
Предположим, что верхняя строка таблицы содержит истинные значения переданных кодов. Из таблицы 1 видно, что, если ошибки случаются в позициях, соответствующих битам кодов из левой колонки, можно определить истинное значение полученного кода. Для этого достаточно полученный код сложить с кодом в левой колонке посредством операции XOR.
Синдром равен произведению левой колонки (CL "cosetleader") стандартного массива на транспонированную матрицу контроля четности HT.
| Синдром = CL . HT | Левая колонка стандартного массива |
Чтобы преобразовать полученный код в правильный, нужно умножить полученный код на транспонированную матрицу проверки четности, с тем чтобы получить синдром. Полученное значение левой колонки стандартного массива добавляется (XOR!) к полученному коду, чтобы получить его истинное значение. Например, если мы получили 001100, умножаем этот код на HT:
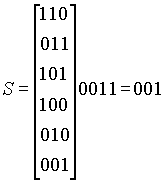
этот результат указывает на место ошибки, истинное значение кода получается в результате операции XOR:
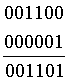
под горизонтальной чертой записано истинное значение кода.
Транспортировка данных подвержена влиянию шумов и наводок, которые вносят искажения. Если вероятность повреждения данных мала, достаточно зарегистрировать сам факт искажения и повторить передачу поврежденного фрагмента.
Когда вероятность искажения велика, например, в каналах коммуникаций с геостационарными спутниками, используются методы коррекции ошибок. Одним из таких методов является FEC (ForwardErrorCorrection, иногда называемое канальным кодированием [1]). Технология FEC последнее время достаточно широко используется в беспроводных, локальных сетях (WLAN). Существуют две основные разновидности FEC: блочное кодирование и кодирование по методу свертки.
Блочное кодирование работает с блоками (пакетами) бит или символов фиксированного размера. Метод свертки работает с потоками бит или символов произвольной протяженности. Коды свертки при желании могут быть преобразованы в блочные коды.
Существует большое число блочных кодов, одним из наиболее важных является алгоритм Рида-Соломона, который используется при работе с CD, DVD и жесткими дисками ЭВМ. Блочные коды и коды свертки могут использоваться и совместно.
Тема 15: Основная теорема Шеннона о кодировании для канала с помехами.
При отсутствии помех ошибки при передаче могут возникать только за счет неоднозначного кодирования сообщений. Рассмотрим теперь ситуацию, когда в канале действуют помехи, вызывающие искажения передаваемых символов. Возникающие при этом ошибки носят случайный характер, они действуют при любой скорости передачи сообщений через канал, в том числе, когда Vu<Vk.
Возникает вопрос, возможен ли такой способ кодирования, при котором сообщения передаются через канал без ошибок с некоторой ненулевой скоростью Vk.0 (действие ошибок полностью устраняется при кодировании)? В первой главе рассматривались методы помехоустойчивости кодирования, основанные на введении избыточности. Однако для полного устранения ошибок их применение потребовало бы введения бесконечной избыточности, что привело бы к снижению скорости передачи сообщений до нуля.
Тем не менее вторая теорема Шеннона утверждает, что такой способ возможен. Тогда возникает следующий вопрос: чем определяется максимальная скорость передачи сообщений по каналу с помехами? Оказывается, что, как и для канала без помех, она определяется соотношением информационных характеристик источника и канала.
Вторая теорема Шеннона: для канала с помехами существует такой способ кодирования, при котором обеспечивается безошибочная передача всех сообщений источника, если только пропускная способность канала превышает производительность источника, т.е. Ck>Vu.
Возникающая ситуация поясняется на рис. 19. На вход канала поступают типичные последовательности источника АТ.Они кодируются последовательностями канала, причем для этой цели используется только часть возможных последовательностей канала Ак. Под действием помех входные последовательности изменяются и переходят в выходные последовательности канала Вк, вообще говоря, не совпадающие с переданными.
| Получив одну из последовательностей Вк на выходе канала, мы должны принять решение относительно переданной последовательности. Как это сделать? Разобьем множество Вк на непересекающиеся подмножества Sk так, чтобы каждой переданной последовательности соответствовало своё подмножество Sk.. При этом выберем подмножества так, чтобы для каждой вход ной последовательности вероятность попадания в своё подмножество была больше, чем в остальные. Принимая последовательность на выходе, смотрим, к какому подмножеству она относится, и в соответствии с этим принимаем решение о переданной типичной последовательности. |
Очевидно, что при этом велика вероятность правильно определить переданную последовательность, однако, возможны и ошибки. Ошибка возникает, если входная последовательность перейдет в несоответствующее ей множество Sk (на рис. 19 показан этот случай). Передача будет всегда безошибочной, если удастся так выбрать входные последовательности канала и разбиение Sk, что переходы в несоответствующие подмножества будут невозможны или, по крайней мере, будут иметь сколь угодно малую вероятность для больших Т. Возможна ли такая ситуация? Оказывается возможна.
Теорема Шеннона для канала с помехами не указывает конкретного способа кодирования, обеспечивающего достоверную передачу информации со скоростью сколь угодно близкой к пропускной способности канала, а лишь указывает на принципиальное существование такого способа. Кроме того, как и в первой теореме, кодирование будет сопровождаться задержкой сообщений не менее 2Т, где. Поэтому идеальное кодирование технически нереализуемо. Однако из формулы для вероятности ошибки вытекает крайне важный практический вывод: достоверность передачи сообщений тем выше, чем больше длительность кодируемой последовательности и чем менее эффективно используется пропускная способность канала, т.е. чем больше запас Ck-Vu.
Теорема Шеннона для канала с помехами оказала огромное влияние на становление правильных взглядов на возможности передачи сообщений и на разработку технически реализуемых методов помехоустойчивого кодирования. Шеннон показал, что для безошибочной передачи сообщений вовсе не обязательно вводить бесконечную избыточность и уменьшать скорость передачи информации до нуля. Достаточно ввести в сообщения источника такую избыточность, которая равна потерям количества информации в канале из-за действия помех.
Тема 16: Помехозащищенности передачи и приема данных.
Помехоустойчивость линии — способность линии уменьшать уровень помех, создаваемых во внешней среде и на внутренних проводниках. Эта способность целиком и полностью зависит от:
§ характеристик используемой физической среды
§ средств линии, предназначенных для экранирования и подавления помех самой линии
Наименьшим является показатель помехоустойчивости у радиолиний, гораздо большей устойчивостью обладают кабельные линии и наилучшей — волоконно-оптические линии, малочувствительные ко внешнему электромагнитному излучению. Стандартными способами уменьшения помех, появляющихся из-за внешних электромагнитных полей, являются методы экранирования и/или скручивания проводников.
Перекрестные наводки на ближнем конце
Перекрестные наводки на ближнем конце (NearEndCrossTalk — NEXT) определяют помехоустойчивость кабеля к внутренним источникам помех. Внутренними называются помехи, возникающие при передаче электромагнитного сигнала по паре проводников, которые наводят на другую пару проводников сигнал помехи. В случае, когда ко второй паре подключен приемник, то наведенная помеха может быть принята за полезный сигнал.
Показатель NEXT рассчитывается следующим образом:
NEXT = 10 logРвых/Рнав,
где Рвых — мощность выходного сигнала, Рнав — мощность наведенного сигнала. Выражается в децибелах
Интерпретация показателя NEXT
Чем меньше значение NEXT, тем лучше кабель. Например, для витой пары категории 5 значение NEXT должно быть не более −27 дБ при частоте 100 МГц.
Показатель NEXT обычно используется применительно к кабелю, состоящему из нескольких витых пар, так как в этом случае взаимные наводки одной пары на другую могут достигать значительных величин. Для коаксиального кабеля, с одной экранированной жилой, этот показатель не рассчитывается, также как и для двойного, в силу высокой защищенности каждого из элементов в составе кабеля. Оптические волокна обладают высокой степенью защиты и практически не создают помех друг для друга.
PowerSUM
В Современных технологиях используется передача данных по нескольким витым парам единовременно. Ввиду этих тенденций, для определения помехоустойчивости стал применяться показатель PowerSUM. Этот показатель — модификация NEXT. Он отражает суммарную мощность перекрестных наводок от всех передающих пар в кабеле.
Достоверность передачи данных. BER
Достоверность передачи данных характеризует вероятность получить искажение для передаваемого бита данных. Часто этот показатель называют интенсивностью битовых ошибок (BitErrorRate, BER). Величина BER для каналов связи без дополнительных средств защиты от ошибок составляет, 10−4 — 10−6, в оптоволокне — 10−9. Значение BER в 10−4 говорит о том, что в среднем из 10000 бит искажается значение одного бита. Искажения бит происходят как из-за наличия помех на линии, так и по причине искажений формы сигнала ограниченной полосой пропускания линии. Для повышения достоверности передаваемых данных нужно повышать степень помехозащищенности линии, снижать уровень перекрестных наводок в кабеле, а также использовать более широкополосные линии связи.
Date: 2015-08-07; view: 1488; Нарушение авторских прав