Производительность источника - количество бит, вырабатываемых в единицу времени - 1 секунду

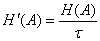
Скорость передач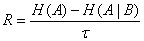и или ;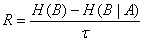

Скорость передачи источника:

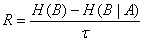[бит/сек],

Емкость канала (пропускная способность канала) - это максимальное

количество бит, передаваемое в единицу времени – секунду.

Пропускная способность – максимальная скорость передачи.

C=maxR

Емкость канала источника:

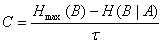[бит/сек],

Коэффициент эффективности дискретного канала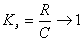

Чем больше коэффициент эффективности дискретного канала стремится к единице, тем эффективнее канал и тем меньше информационные потери на нём.

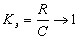
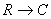
Тема 10: Основныемодели источника дискретных сообщений: источник с памятью и без памяти. Производительность источника дискретных сообщений.

Источник сообщений - это то, что вырабатывает сообщения. Это устная речь, письмо, газеты, книги, сообщения по радио, телевидению, результаты измерений, представленные в виде последовательности цифр и т. д. Сообщение может поступать в форме последовательности каких-либо кодовых знаков.

Нас интересует источник с математической точки зрения, так чтобы можно было отличать источники друг от друга с каких то обобщенных позиций.

С математической точки зрения, под источником информации понимают множество возможных сообщений с заданной на этом множестве вероятностной мерой.

Различают дискретные источники и непрерывные.

Тема 11: Свойства эргодических последовательностей символов. Избыточность. Производительность источника дискретных сообщений.

При доказательстве основных положений теории информацииШенноном использовалась модель, называемая эргодическим источником сообщений. Предполагается, что создаваемые им сообщения математически можно представить в виде эргодической случайной последовательности. Такая последовательность, как известно, удовлетворяет условиям стационарности и эргодичности. Первое означает, что вероятности отдельных знаков и их сочетаний не зависят от расположения последних по длине сообщения. Из второго следует, что статистические закономерности, полученные при исследовании одного достаточно длинного сообщения с вероятностью, близкой к единице, справедливы для всех сообщений, создаваемых источником. Из статистических характеристик в данном случае нас интересует средняя неопределенность в расчете на один знак последовательности.

Уменьшение энтропии источника с увеличением статисти­ческой взаимосвязи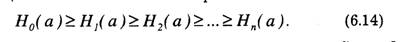

можно рассматривать как снижение информационной емкости сообщений. Одно и то же сообщение при наличии взаимосвязи содержит в среднем меньше информации, чем при ее отсутствии.

Иначе говоря, если источник создает последовательность сообщений, обладающих статистической связью, и характер этой связи известен, то часть сообщений, выдаваемая источником, является избыточной, так как она может быть восстановлена по известным статистическим связям. Появляется возможность передавать сообщения в сокращенном виде без потери информации, содержащейся в них.

Например, при передаче телеграммы мы исключаем из текста союзы, предлоги, знаки препинания, так как они легко восстанавливаются при чтении телеграммы на основании известных правил построения фраз и слов.

Таким образом, любой источник зависимых сообщений, как принято говорить, обладает избыточностью. Количе­ственное определение избыточности может быть получено из следующих соображений. Для того чтобы передать количе

называется коэффициентом сжатия. Он показывает, до ка­кой величины можно сжать передаваемые сообщения, если устранить избыточность. Источник, обладающий избыточнос­тью, передает излишнее количество сообщений. Это увеличи­вает продолжительность передачи и снижает эффективность использования канала связи. Сжатие сообщений можно осу­ществить посредством соответствующего кодирования. Информацию необходимо передавать такими сообщениями, ин­формационная емкость которых используется наиболее пол­но. Этому условию удовлетворяют равновероятные и незави­симые сообщения.

Вместе с тем избыточность источника не всегда является отрицательным свойством. Наличие взаимосвязи между бук­вами текста дает возможность восстанавливать его при искажении отдельных букв, т. е. использовать избыточность для повышения достоверности передачи информации.

Тема 12: Информационные характеристики дискретных каналов связи. Модели дискретных каналов: каналы с памятью и без памяти, стационарные и нестационарные.

Модели дискретных каналов. Дискретным каналом называют совокупность средств, предназначенных для передачи дискретных сигналов. Такие каналы широко используются, например, при передаче данных, в телеграфии, радиолокации.

Дискретные сообщения, состоящие из последовательности знаков алфавита источника сообщений (первичного алфавита) преобразуются в кодирующем устройстве в последовательности символов.

Объем m алфавита символов (вторичного алфавита), как правило, меньше объема l алфавита знаков, но они могут и совпадать.

Материальным воплощением символа является элементарный сигнал,

получаемый в процессе манипуляции — дискретного изменения определенного параметра переносчика информации. Элементарные сигналы

формируются с учетом физических ограничений, накладываемых конкретной

линией связи. В результате манипуляции каждой последовательности символов ставится в соответствие сложный сигнал. Множество сложных сигналов конечно. Они различаются числом, составом и взаимным расположением элементарных сигналов.

Термины «элементарный сигнал» и «символ», так же как «сложный сигнал» и «последовательность символов», в дальнейшем будут использоваться как синонимы.

Информационная модель канала с помехами задается множеством символов на его входе и выходе и описанием вероятностных свойств передачи отдельных символов. В общем случае канал может иметь множество состояний и переходить из одного состояния в другое как с течением времени, так и в зависимости от последовательности передаваемых символов.

В каждом состоянии канал характеризуется матрицей условных вероятностей ρ(juiv) того, что переданный символ ui будет воспринят на выходе как символ νj. Значения вероятностей в реальных каналах зависят от

многих различных факторов: свойств сигналов, являющихся физическими

носителями символов (энергия, вид модуляции и т.д.), характера и интенсивности воздействующих на канал помех, способа определения сигнала на приемной стороне.

При наличии зависимости переходных вероятностей канала от времени, что характерно практически для всех реальных каналов, он называется нестационарным каналом связи. Если эта зависимость несущественна, используется модель в виде стационарного канала, переходные вероятности которого не зависят от времени. Нестационарный канал может быть представлен рядом стационарных каналов, соответствующих различным интервалам времени.

Канал называется с «памятью» (с последействием), если переходные вероятности в данном состоянии канала зависят от его предыдущих состояний. Если переходные вероятности постоянны, т.е. канал имеет только одно состояние, он называется стационарным каналом без памяти. Под k-ичным каналом подразумевается канал связи, у которого число различных символов на входе и выходе одинаково и равно k.Стационарный дискретный двоичный канал без памяти однозначно определяется четырьмя условными вероятностями: р(0/0), р(1/0), р(0/1), р(1/1). Такую модель канала принято изображать в виде графа, представленного на рис. 4.2, где р(0/0) и р(1/1) — вероятности неискаженной передачи символов, а р(0/1) и р(1/0) — вероятности искажения (трансформация) символов 0 и 1 соответственно.

Если вероятности искажения символов можно принять равными, т. е.

то такой канал называют двоичным симметричным каналом

[при р(0/1)≠ ≠ р(1/0) канал называется несимметричным]. Символы на его выходе правильно принимают с вероятностью ρ и неправильно — с вероятностью 1—p = q. Математическая модель упрощается.

Именно этот канал исследовался наиболее интенсивно не столько в силу своей практической значимости (многие реальные каналы описываются им весьма приближенно), сколько в силу простоты математического описания.

Важнейшие результаты, полученные для двоичного симметрического

канала, распространены на более широкие классы каналов.Следует отметить еще одну модель канала, которая в последнее время приобретает все большее значение. Это дискретный канал со стиранием. Для него характерно, что алфавит выходных символов отличается от алфавита входных символов. На входе, как и ранее, символы 0 и 1, а на выходе канала фиксируются состояния, при которых сигнал с равным основанием может быть отнесен как к единице, так и к нулю. На месте такого символа не ставится ни нуль, ни единица: состояние отмечается дополнительным символом стирания S. При декодировании значительно легче исправить такие символы, чем ошибочно

определенные.

Скорость передачи информации по дискретному каналу.Характеризуя дискретный канал связи, используют два понятия скорости передачи: технической и информационной.Под технической скоростью передачи VT, называемой также скоростью манипуляции, подразумевают число элементарных сигналов (символов), передаваемых по каналу в единицу времени. Она зависит от свойств линии связи и быстродействия аппаратуры канала.

С учетом возможных различий в длительностях символов скорость

где ср

τ — среднее значение длительности символа.

При одинаковой продолжительности τ всех передаваемых символов ср

τ

= τ.

Единицей измерения технической скорости служит бод — скорость, при которой за одну секунду передается один символ.

Информационная скорость, или скорость передачи информации, определяется средним количеством информации, которое передается по каналу в единицу времени. Она зависит как от характеристик данного канала связи, таких, как объем алфавита используемых символов, техническая скорость их передачи, статистические свойства помех в линии, так и от вероятностей поступающих на вход символов и их статистической взаимосвязи. При известной скорости манипуляции VT скорость передачи информации по каналу Ī(V,U) задается соотношением

где I(V,U) — среднее количество информации, переносимое одним символом.

Пропускная способность дискретного канала без помех. Для теории и практики важно выяснить, до какого предела и каким путем можно повысить скорость передачи информации по конкретному каналу связи. Предельные возможности канала по передаче информации характеризуются его пропускной способностью.

Пропускная способность канала Сд равна той максимальной скорости

передачи информации по данному каналу, которой можно достигнуть при

самых совершенных способах передачи и приема:

При заданном алфавите символов и фиксированных основных характеристиках канала (например, полосе частот, средней и пиковой мощности передатчика) остальные характеристики должны быть выбраны такими, чтобы обеспечить наибольшую скорость передачи по нему элементарных сигналов, т. е. обеспечить максимальное значение VТ.

Максимум среднего количества информации, приходящейся на один символ принятого сигнала I(V,U), определяется на множестве распределений вероятностей между символами u u

i

um

...... 1

Пропускная способность канала, как и скорость передачи информации

по каналу, измеряется числом двоичных единиц информации в секунду (дв.

ед./с).

Так как в отсутствие помех имеет место взаимно-однозначное соответствие между множеством символов {ν} на выходе канала и {u} наего

входе, то I(V,U) = =I(U,V) = H(U). Максимум возможного количества информации на символ равен log m, где m — объем алфавита символов, откуда пропускная способность дискретного канала без помех

Следовательно, для увеличения скорости передачи информации по дискретному каналу без помех и приближения ее к пропускной способности канала последовательность букв сообщения должна подвергнуться такому преобразованию в кодере, при котором различные символы в его выходной последовательности появлялись бы по возможности равновероятно, а статистические связи между ними отсутствовали бы.

Расширение объема алфавита символов m приводит к повышению пропускной способности канала (рис. 4.4), однако возрастает и сложность технической реализации.

Пропускная способность дискретного канала с помехами. При наличии помех соответствие между множествами символов на входе и выходе канала связи перестает быть однозначным. Среднее количество информации I(V,U), передаваемое по каналу одним символом, определяется в этом случае соотношением

Если статистические связи между символами отсутствуют, энтропия

сигнала на выходе линии связи равна

При наличии статистической связи энтропию определяют с использованием цепей Маркова. Поскольку алгоритм такого определения ясен и нет необходимости усложнять изложение громоздкими формулами, ограничимся здесь только случаем отсутствия связей.

Апостериорная энтропия характеризует уменьшение количества переданной информации вследствие возникновения ошибок. Она зависит как от статистических свойств последовательностей символов, поступающих на вход канала связи, так и от совокупности переходных вероятностей, отражающих вредное действие помехи.

Если объем алфавита входных символов u равен m1, а выходных символов υ — m2, то

Подставив выражения (4.18) и (4.19) в (4.17) и проведя несложные

преобразования, получим

Скорость передачи информации по каналу с помехами

Считая скорость манипуляции VT предельно допустимой при заданных

технических характеристиках канала, величину I(V,U) можно

максимизировать, изменяя статистические свойства последовательностей

символов на входе канала посредством преобразователя (кодера канала). Получаемое при этом предельное значение СД скорости передачи

информации по каналу называют пропускной способностью дискретного

канала связи с помехами:

где р{u} — множество возможных распределений вероятностей входных

сигналов.

Важно подчеркнуть, что при наличии помех пропускная способность

канала определяет наибольшее количество информации в единицу времени,

которое может быть передано со сколь угодно малой вероятностью ошибки.

В гл. 6 показано, что к пропускной способности канала связи с

помехами можно приблизиться, кодируя эргодическую последовательность

букв источника сообщений блоками такой длины, при которой справедлива

теорема об асимптотическойравновероятности длинных

последовательностей.

Произвольно малая вероятность ошибки оказывается достижимой

только в пределе, когда длина блоков становится бесконечной.

При удлинении кодируемых блоков возрастает сложность технической

реализации кодирующих и декодирующих устройств и задержка в передаче

сообщений, обусловленная необходимостью накопления требуемого числа

букв в блоке. В рамках допустимых усложнений на практике при

кодировании могут преследоваться две цели: либо при заданной скорости

передачи информации стремятся обеспечить минимальную ошибку, либо при

заданной достоверности — скорость передачи, приближающуюся к

пропускной способности канала.

Предельные возможности канала никогда не используются полностью.

Степень его загрузки характеризуется коэффициентом использования канала

где — производительность источника сообщений; СД — пропускная

способность канала связи.Поскольку нормальное функционирование канала возможно, как

показано далее, при изменении производительности источника в пределах

, теоретически может изменяться в пределах от 0 до 1.

Пример 4.4. Определить пропускную способность двоичного

симметричного канала (ДСК) со скоростью манипуляции VT в

предположении независимости передаваемых символов.

Запишем соотношение (4.19) в следующем виде:

Воспользовавшись обозначениями на графе (рис. 4.5), можем записать

Так как-то

Величина HU(V) не зависит от вероятностей входных символов, что является следствием симметрии канала. Следовательно, пропускная способность

Максимум H(V) достигается при равенстве вероятностей появления

символов, он равен 1. При увеличении вероятности трансформации символа с 0 до 1/2 СД(р) уменьшается от 1 до 0. Если ρ = 0, то шум в канале отсутствует и его пропускная способность равна 1. При р=1/2 канал бесполезен, так как

значения символов на приемной стороне с равным успехом можно

устанавливать по результатам подбрасывания монеты (герб—1, решетка —

0). Пропускная способность канала при этом равна нулю

Тема 13: Основная теорема Шеннона о кодировании в канале без помех

Рассмотрим две фундаментальные теоремы идеального кодирования, носящие имя Шеннона. Первая из них рассматривает случай отсутствия помех в канале, вторая учитывает наличие помех, приводящих к ошибкам.

Рассмотрим проблему согласования источника сообщений и канала при передаче последовательности сообщений. Пусть источник сообщений выдает сообщения с некоторой скоростью (сообщений/ед. времени), называемой технической производительностью источника. Пусть по каналу можно передавать без искажений сообщения со скоростью, не превышающей некоторую величину (сообщений/ед. времени), называемую технической пропускной способностью канала. Очевидно, что если выполняется условие <, то канал успевает передать все сообщения, поступающие на его вход от источника, и передача будет вестись без искажений. Что произойдет, если >? Можно ли в этом случае обеспечить передачу без искажений? Если исходить только из технических характеристик, то, очевидно, нельзя. А если учесть информационные характеристики? Ведь нам известно, что если последовательность обладает информационной избыточностью, то её можно сжать, применив методы экономного кодирования. Рассмотрим подробнее такую возможность.

Пусть Vu - (информационная) производительность источника, т.е. количество информации, производимое источником в единицу времени; Ck — (информационная) пропускная способность канала, т.е. максимальное количество информации, которое способен передать канал без искажений за единицу времени. Первая теорема Шеннона утверждает, что безошибочная передача сообщений определяется соотношением Vu и Ck.

Первая теорема Шеннона: если пропускная способность канала без помех превышает производительность источника сообщений, т.е. удовлетворяется условие Ck >Vu,

то существует способ кодирования и декодирования сообщений источника, обеспечивающий сколь угодно высокую надежность передачи сообщений. В противном случае, т.е. если Ck <Vu

Такого способа нет.

Таким образом, идеальное кодирование по Шеннону по существу представляет собой экономное кодирование последовательности сообщений при безграничном укрупнении сообщений. Такой способ кодирования характеризуется задержкой сообщений

поскольку кодирование очередной типичной последовательности может начаться только после получения последовательности источника длительностью T, а декодирование — только когда принята последовательность из канала той же длительности T. Поскольку требуется, то идеальное кодирование требует бесконечной задержки передачи информации. В этом причина техническойнереализуемости идеального кодирования по Шеннону. Тем не менее, значение этого результата, устанавливающего предельные соотношения информационных характеристик источника и канала для безошибочной передачи сообщений, весьма велико. Исторически именно теорема Шеннона инициировала и определила развитие практических методов экономного кодирования.

Тема 14: Блочное кодирование и его преимущества.

Блочный кодер обозначается (K2,K1), где K1 - число символов в блоке входной последовательности, а K2 - число символов в блоке выходной последовательности. Отношение R=K1/K2 носит наименование скорости кодирования (codingrate) и характеризует меру избыточности, вносимую кодером.

При блочном кодировании в стандарте TETRA используется двоичный систематический кодер, т. е. кодер, у которого каждый символ входной и выходной последовательности соответствует одному биту, а в состав блока выходной информации полностью включается блок входной информации, который дополняется p-битовым кодом циклического контроля избыточности (CRC - CyclicRedundancyCheck). Таким образом, K1 битов типа 1 преобразуются в K2 бита типа 2, где K2=K1+p.

CRC-коды вычисляются по правилу

F(X) = X^n-K1M(X) mod G(X),

гдеM(X)=b₁(1)X^K1-1 + b₁(2)X^K1-2 +... + b₁(K1-1)X^! + b₁(K1),

G(X) - формирующий полином, различный для разных логических каналов;
n-K1 - количество создаваемых битов четности.

Многочлен F(X) является многочленом степени (n-K1-1) с

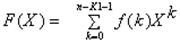
коэффициентами f(0), f(1),.., f(n-K1-1), т. е.

Тогда K2 бит типа 2 имеют вид:
b₂(k) = b₁(k) при k = 1,2,.., K1
b₂(k) = f(k-K1-1) при k = K1+1, K1+2,.., n.

Порождающий полином для канала речевого трафика имеет вид:

G(X) = 1 + X³ +X⁷,

для остальных каналов:G(X) = 1 + X⁵ + X¹² + X¹⁶.

Для одного из логических каналов - канала назначения доступа AACH - используется блочное кодирование на основе кода Рида-Маллера. Коды Рида-Маллера представляют собой класс линейных кодов с простым описанием и декодированием, осуществляемым методом простого голосования.

Порождающая матрица кода Рида-Маллера r-го порядка длиной 2^m определяется как совокупность блоков

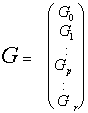
где G₀ - вектор размерности n=2^m, состоящий из одних единиц; G_p - (m х 2^m)- матрица, содержащая в качестве столбцов все двоичные m-последовательности; строки матрицы G_pполучены из строк матрицы G₁ как все возможные произведения p строк из G₁.

При блочном кодировании канала AACH стандарта TETRA 14 бит входной информационной последовательности должно преобразовываться в 30-разрядный выходной блок в соответствии с уравнением

[b₂(1), b₂(2),..,b₂(30)] = [b₁(1), b₁(2),..,b₁(14)] G,

где G - порождающая матрица, имеющая вид

G = [I₁₄G_RM],

где I₁₄ - единичная матрица размером 14х14, а GRM - порождающая матрица кода Рида-Маллера размерностью 16х14.

Это означает, что при блочном кодировании AACH первые 14 бит выходной последовательности соответствуют битам входного информационного блока, а последующие 16 бит образуются с помощью кода Рида-Маллера.

Date: 2015-08-07; view: 1458; Нарушение авторских прав