
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Определение количества информации
|
|
Пусть сообщение состоит из одного символа. Если вероятности появления всех символов одинаковы и равны P = 1/m, то количество информации, которое переносит символ, можно выразить как
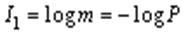 .
.
Здесь количество информации связано с вероятностью появления символа. В реальных сообщениях символы 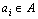 появляются с различными вероятностями
появляются с различными вероятностями 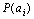 , поэтому
, поэтому
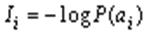 .
.
Среднее количество информацииH(A), которое приходится на один символ источника сообщений можно найти усреднением по всему объему алфавита
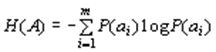 . (1)
. (1)
Эта величина называется энтропией источника дискретных сообщений. Формула (1) носит название формулы Шеннона.
Энтропия рассматривается как мера неопределенности в поведении источника сообщений. При вероятностном подходе состояние источника информации характеризуется неопределенностью. Неопределенность снижается при приеме сообщения, т.е. получении информации. Поэтому получаемая информация, приходящаяся в среднем на один символ источника сообщений, количественно определяет степень уменьшения неопределенности.
Энтропия является непрерывной функцией от вероятностей появления символов и обладает следующими свойствами:
· Энтропия источника дискретных сообщений есть величина вещественная, ограниченная и неотрицательная.
· Энтропия равна нулю, если с вероятностью единица выбирается один и тот же символ (неопределенность в поведении источника отсутствует).
· Энтропия максимальна, если все символы источника появляются независимо и с одинаковой вероятностью:
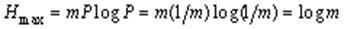 .
.
Если символы являются взаимосвязанными (коррелированными друг с другом), то используется понятие условной энтропии
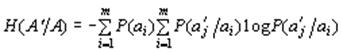 , (2)
, (2)
где 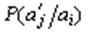 – условная вероятность появления символа
– условная вероятность появления символа 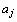 после символа
после символа 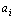 .
.
Из-за корреляционных связей символов и неравновероятного их появления в реальных сообщениях снижается среднее количество информации, которое переносит один символ. Эти потери информации характеризуются коэффициентом избыточности
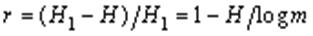 ,
,
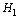 – максимальное количество информации, которое может переносить один символ, H – количество информации, которое переносит один символ в реальных сообщениях (например, для европейских языков
– максимальное количество информации, которое может переносить один символ, H – количество информации, которое переносит один символ в реальных сообщениях (например, для европейских языков  ).
).
Наиболее часто основание логарифма в (1) принимают равным 2. При этом единицей количества информации является бит (binarydigit).
Производительностью источника сообщений называется среднее количество информации, выдаваемой источником в единицу времени, а именно
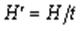 [бит/с].
[бит/с].
Для каналов передачи информации вводят аналогичную характеристику – скорость передачи информации C. Максимальное её значение называется пропускной способностью канала. Для дискретного канала
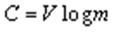 [бит/с], (3)
[бит/с], (3)
где V – скорость передачи электрических кодовых сигналов.
Тема 3: Энтропия как мера неопределенности выбора. Сообщение как совокупность сведений о состоянии физической системы.
Любое сообщение, с которым мы имеем дело в теории информации, представляет собой совокупность сведений о некоторой физической системе.
Например, на вход автоматизированной системы управления производственным цехом может быть передано сообщение о нормальном или повышенном проценте брака, о химическом составе сырья или температуре в печи. На вход системы управления средствами противовоздушной обороны может быть передано сообщение о том, что в воздухе находятся две цели, летящие на определенной высоте, с определенной скоростью. На тот же вход может быть передано сообщение о том, что на определенном аэродроме в данный момент находится такое-то количество истребителей в боевой готовности, или что аэродром выведен из строя огневым воздействием противника, или что первая цель сбита, а вторая продолжает полет с измененным курсом. Любое из этих сообщений описывает состояние какой-то физической системы.
Очевидно, если бы состояние физической системы было известно заранее, не было бы смысла передавать сообщение. Сообщение приобретает смысл только тогда, когда состояние системы заранее неизвестно, случайно.
Поэтому в качестве объекта, о котором передается информация, мы будем рассматривать некоторую физическую систему 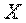 , которая случайным образом может оказаться в том или ином состоянии, т. е. систему, которой заведомо присуща какая-то степень неопределенности. Очевидно, сведения, полученные о системе, будут, вообще говоря, тем ценнее и содержательнее, чем больше была неопределенность системы до получения этих сведений («априори»).
, которая случайным образом может оказаться в том или ином состоянии, т. е. систему, которой заведомо присуща какая-то степень неопределенности. Очевидно, сведения, полученные о системе, будут, вообще говоря, тем ценнее и содержательнее, чем больше была неопределенность системы до получения этих сведений («априори»).
Возникает естественный вопрос: что значит «большая» или «меньшая» степень неопределенности и чем можно ее измерить?
Чтобы ответить на этот вопрос, сравним между собой две системы, каждой из которых присуща некоторая неопределенность.
В качестве первой системы возьмем монету, которая в результате бросания может оказаться в одном из двух состояний: 1) выпал герб и 2) выпала цифра.
В качестве второй - игральную кость, у которой шесть возможных состояний: 1, 2, 3, 4, 5 и 6.
Спрашивается, неопределенность какой системы больше?
Очевидно, второй, так как у нее больше возможных состояний, в каждом из которых она может оказаться с одинаковой вероятностью.
Может показаться, что степень неопределенности определяется числом возможных состояний системы. Однако в общем случае это не так.
Рассмотрим, например, техническое устройство, которое может быть в двух состояниях: 1) исправно и 2) отказало. Предположим, что до получения сведений (априори) вероятность исправной работы устройства 0,99, а вероятность отказа 0,01. Такая система обладает только очень малой степенью неопределенности: почти наверное можно предугадать, что устройство будет работать исправно. При бросании монеты тоже имеется два возможных состояния, но степень неопределенности гораздо больше. Мы видим, что степень неопределенности физической системы определяется не только числом ее возможных состояний, но и вероятностями состояний.
Перейдем к общему случаю. Рассмотрим некоторую систему 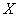 , которая может принимать конечное множество состояний:
, которая может принимать конечное множество состояний: 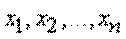 с вероятностями
с вероятностями 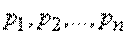 , где
, где
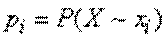 (1)
(1)
- вероятность того, что система 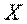 примет состояние
примет состояние 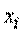 (символом
(символом 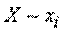 обозначается событие: система находится в состоянии
обозначается событие: система находится в состоянии 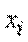 ). Очевидно,
). Очевидно, 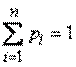 .
.
Запишем эти данные в виде таблицы, где в верхней строке перечислены возможные состояния системы, а в нижней - соответствующие вероятности:
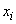
| 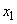
| 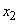
| 
| 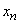
|
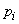
| 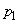
| 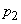
| 
| 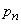
|
Эта табличка по написанию сходна с рядом распределения прерывной случайной величины 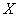 с возможными значениями
с возможными значениями 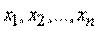 , имеющими вероятности
, имеющими вероятности 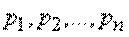 . И действительно, между физической системой
. И действительно, между физической системой 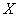 с конечным множеством состояний и прерывной случайной величиной много общего; для того чтобы свести первую ко второй, достаточно приписать каждому состоянию какое-то числовое значение (скажем, номер состояния). Подчеркнем, что для описания степени неопределенности системы совершенно неважно, какие именно значения
с конечным множеством состояний и прерывной случайной величиной много общего; для того чтобы свести первую ко второй, достаточно приписать каждому состоянию какое-то числовое значение (скажем, номер состояния). Подчеркнем, что для описания степени неопределенности системы совершенно неважно, какие именно значения 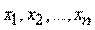 записаны в верхней строке таблицы; важны только количество этих значений и их вероятности.
записаны в верхней строке таблицы; важны только количество этих значений и их вероятности.
В качестве меры априорной неопределенности системы (или прерывной случайной величины 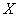 ) в теории информации применяется специальная характеристика, называемая энтропией. Понятие об энтропии является в теории информации основным.
) в теории информации применяется специальная характеристика, называемая энтропией. Понятие об энтропии является в теории информации основным.
Энтропией системы называется сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей, взятая с обратным знаком:
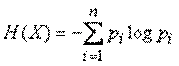 (2)
(2)
Энтропия 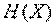 , как мы увидим в дальнейшем, обладает рядом свойств, оправдывающих ее выбор в качестве характеристики степени неопределенности. Во-первых, она обращается в нуль, когда одно из состояний системы достоверно, а другие - невозможны. Во-вторых, при заданном числе состояний она обращается в максимум, когда эти состояния равновероятны, а при увеличении числа состояний - увеличивается. Наконец, и это самое главное, она обладает свойством аддитивности, т. е. когда несколько независимых систем объединяются в одну, их энтропии складываются.
, как мы увидим в дальнейшем, обладает рядом свойств, оправдывающих ее выбор в качестве характеристики степени неопределенности. Во-первых, она обращается в нуль, когда одно из состояний системы достоверно, а другие - невозможны. Во-вторых, при заданном числе состояний она обращается в максимум, когда эти состояния равновероятны, а при увеличении числа состояний - увеличивается. Наконец, и это самое главное, она обладает свойством аддитивности, т. е. когда несколько независимых систем объединяются в одну, их энтропии складываются.
Логарифм в формуле может быть взят при любом основании 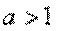 . Перемена основания равносильна простому умножению энтропии на постоянное число, а выбор основания равносилен выбору определенной единицы измерения энтропии. Если за основание выбрано число 10, то говорят о «десятичных единицах» энтропии, если 2 - о «двоичных единицах». На практике удобнее всего пользоваться логарифмами при основании 2 и измерять энтропию в двоичных единицах; это хорошо согласуется с применяемой в электронных цифровых вычислительных машинах двоичной системой счисления.
. Перемена основания равносильна простому умножению энтропии на постоянное число, а выбор основания равносилен выбору определенной единицы измерения энтропии. Если за основание выбрано число 10, то говорят о «десятичных единицах» энтропии, если 2 - о «двоичных единицах». На практике удобнее всего пользоваться логарифмами при основании 2 и измерять энтропию в двоичных единицах; это хорошо согласуется с применяемой в электронных цифровых вычислительных машинах двоичной системой счисления.
В дальнейшем мы будем везде, если не оговорено противное, под символом 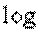 понимать двоичный логарифм.
понимать двоичный логарифм.
В приложении (табл. 6) даны двоичные логарифмы целых чисел от 1 до 100.
Легко убедиться, что при выборе 2 в качестве основания логарифмов за единицу измерения энтропии принимается энтропия простейшей системы 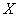 , которая имеет два равновозможных состояния:
, которая имеет два равновозможных состояния:
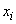
| 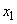
| 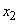
|
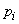
| 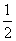
| 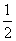
|
Действительно, по формуле (2) имеем:
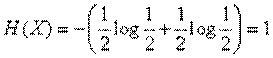 .
.
Определенная таким образом единица энтропии называется «двоичной единицей» и иногда обозначается bit (от английского «binarydigit» - двоичный знак). Это энтропия одного разряда двоичного числа, если он с одинаковой вероятностью может быть нулем или единицей.
Измерим в двоичных единицах энтропию системы 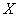 , которая имеет
, которая имеет 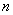 равновероятных состояний:
равновероятных состояний:
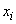
| 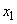
| 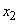
| 
| 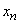
|
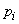
| 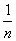
| 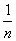
| 
| 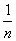
|
Имеем:
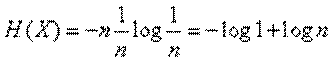
или
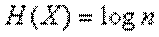 , (3)
, (3)
т. е. энтропия системы с равновозможными состояниями равна логарифму числа состояний.
Например, для системы с восемью состояниями 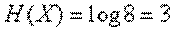 .
.
Докажем, что в случае, когда состояние системы в точности известно заранее, ее энтропия равна нулю. Действительно, в этом случае все вероятности 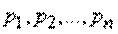 в формуле (2) обращаются в нуль, кроме одной - например
в формуле (2) обращаются в нуль, кроме одной - например 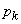 , которая равна единице. Член
, которая равна единице. Член 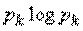 обращается в нуль, так как
обращается в нуль, так как 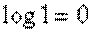 . Остальные члены тоже обращаются в нуль, так как
. Остальные члены тоже обращаются в нуль, так как
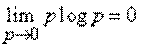 .
.
Докажем, что энтропия системы с конечным множеством состояний достигает максимума, когда все состояния равновероятны. Для этого рассмотрим энтропию системы (2) как функцию вероятностей  и найдем условный экстремум этой функции при условии:
и найдем условный экстремум этой функции при условии:
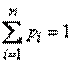 . (4)
. (4)
Пользуясь методом неопределенных множителей Лагранжа, будем искать экстремум функции:
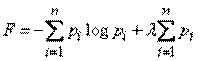 (5)
(5)
Дифференцируя (5) по 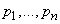 и приравнивая производные нулю, получим систему уравнений:
и приравнивая производные нулю, получим систему уравнений:
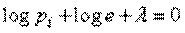
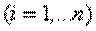
или
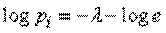
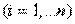 , (6)
, (6)
откуда видно, что экстремум (в данном случае максимум) достигается при равных между собой значениях 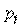 . Из условия (4) видно, что при этом
. Из условия (4) видно, что при этом
 , (7)
, (7)
а максимальная энтропия системы равна:
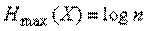 , (8)
, (8)
т. е. максимальное значение энтропии системы с конечным числом состояний равно логарифму числа состояний и достигается, когда все состояния равновероятны.
Вычисление энтропии по формуле (2) можно несколько упростить, если ввести в рассмотрение специальную функцию:
 , (9)
, (9)
где логарифм берется по основанию 2.
Формула принимает вид:
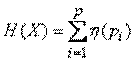 . (10)
. (10)
Функция 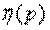 затабулирована; ее значения для
затабулирована; ее значения для  от 0 до 1 через 0,01.
от 0 до 1 через 0,01.
Пример 1. Определить энтропию физической системы, состоящей из двух самолетов (истребителя и бомбардировщика), участвующих в воздушном бою. В результате боя система может оказаться в одном из четырех возможных состояний:
1) оба самолета не сбиты;
2) истребитель сбит, бомбардировщик не сбит;
3) истребитель не сбит, бомбардировщик сбит;
4) оба самолета сбиты.
Вероятности этих состояний равны соответственно 0,2; 0,3; 0,4 и 0,1.
Решение. Записываем условия в виде таблицы:
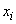
| 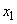
| 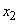
| 
| 
|
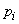
| 0,2 | 0,3 | 0,4 | 0,1 |
По формуле (18.2.10) имеем:
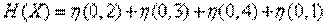 .
.
Пользуясь таблицей 7 приложения, находим
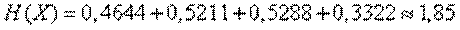 (дв. ед.).
(дв. ед.).
Пример 2. Определить энтропию системы, состояние которой описывается прерывной случайной величиной 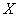 с рядом распределения
с рядом распределения
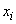
| 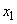
| 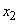
| 
| 
| 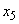
|
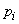
| 0,01 | 0,01 | 0,01 | 0,01 | 0,96 |
Date: 2015-08-07; view: 1878; Нарушение авторских прав