Исследование нелинейных систем методом фазовой плоскости

Основные понятия

Метод фазовой плоскости обычно применяется для анализа нелинейных систем второго порядка при исследовании в них собственных процессов 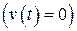или вынужденных при 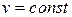. Пусть в нелинейной системе рис. 2.2 передаточная функция имеет вид

. (2.10)

Используем модели (2.7), (2.8) для данного случая и запишем уравнения (2.7) в нормальной форме [1]:

, .

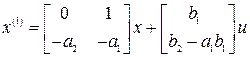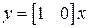Уравнение замкнутой системы (2.8) будет

, .

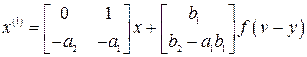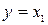Будем полагать, что 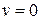, а нелинейность обладает свойством симметрии относительно начала координат (рис 2.3, 2,4), т.е. .

В этом случае уравнения примут вид:

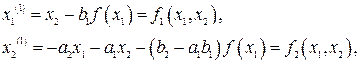(2.11)

где 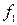, 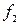– нелинейные функции.

Частным случаем уравнения (2.11) является случай, когда :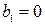

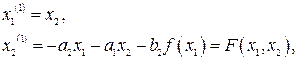(2.12)

который встречается довольно часто.

Характерной особенностью (2.11), (2.12) является то, что координата 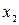является скоростью изменения координаты 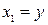, т.е. .

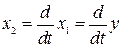Пусть при заданных начальных условиях 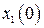, 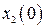определено конкретное (частное) решение 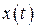уравнения (2.11). В трехмерном пространстве с коорди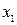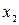натами , , это решение можно изобразить в виде некоторой кривой, которую называют интегральной кривой. Проекция этой кривой на плоскость с координатами 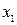, 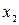также будет некоторой кривой или траекторией, которую будем называть траекторией состояния или фазовой траекторией.

Совокупность фазовых траекторий на плоскости с координатами 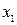, 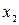будем называть фазовым портретом системы, а саму плоскость – фазовой плоскостью.

При 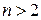все вышесказанное можно обобщить, однако ввиду сложной геометрической интерпретации фазовое пространство и фазовые траектории для этого случая применяются редко.

Найдем уравнения, определяющие фазовые траектории. Для этого в (2.11) разделим почленно второе уравнение на первое, тогда с учетом 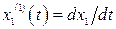, 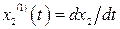получим

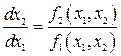. (2.13)

Уравнение (2.13) является нелинейным дифференциальным уравнением первого порядка, в котором 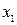является аргументом (независимой переменной). Решение этого уравнения 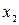(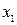) и является искомой фазовой траекторией. Так как в конечном итоге координаты 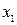и 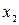зависят от времени , то с течением времени точка на фазовой траектории, которую назовем изображающей точкой, будет двигаться по фазовой траектории.

Для частного случая (2.12) уравнения фазовых траекторий будут иметь вид

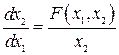. (2.14)

Правила движения изображающей точки по фазовым траекториям на фазовой плоскости 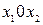, где 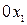– ось абсцисс, 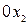– ось ординат:

а) если 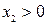, то по фазовой траектории изображающая точка движется слева направо в сторону увеличения 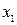, т.к. скорость ;

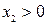б) если 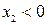, то наоборот – справа налево;

в) ось 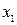фазовая траектория пересекает под прямым углом (свойство справедливо только для уравнения (2.14)).

Рассмотрим качественное соответствие характера поведения интегральной кривой (координат 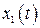, 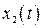) и соответствующих фазовых траекторий. На рис. 2.3 показаны 5 видов процессов : 1 − периодический, 2 − возрастающий колебательный, 3 − затухающий колебательный, 4 − монотонный возрастающий, 5 − монотонный затухающий. На рис. 4 для каждого из них показаны фазовые траектории.

Рис. 2.3

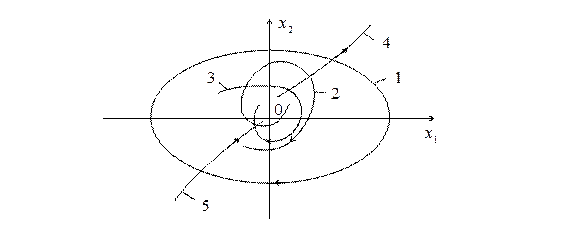
Рис. 2.4

Итак, если известен фазовый портрет системы, то можно качественно оценить характер протекающих в системе процессов: являются ли они затухающими и стремятся к нулю при 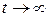либо нет; как затухают – с колебаниями, либо монотонно; являются ли периодическими и т.п.

Date: 2015-08-06; view: 520; Нарушение авторских прав