экстремума, поэтому требуется дополнительное исследование

Пример 1. Исследовать на экстремум функцию f (x, y) = 4 x ² у + 24 хy + у ² + 32 у – 6.

Решение. Область определения D (f) – вся плоскость Оху, f (x, y) дифференцируема в каждой точке М (x; y) 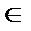D (f).

1. Найдем стационарные точки:

<=> =>

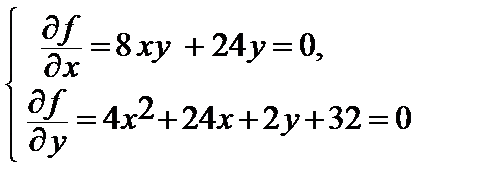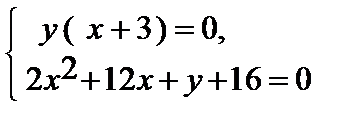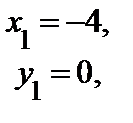
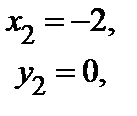
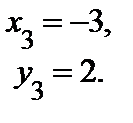
Получили три стационарные точки М ₁(4; 0), М ₂(–2; 0), М ₃(–3; 2 ), лежащие в области D (f).

2. Исследуем все эти точки на достаточность условий экстремума. Сначала определим отдельно

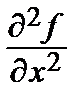= 8 у, 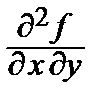= 8 х + 24, 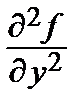= 2. Затем в каждой точке вычислим А, В, С, определим Δ = АС – В ² и А:

а) М ₁(4; 0): А ₁= 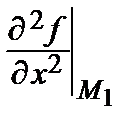= 8 ∙ 0 = 0, В ₁= 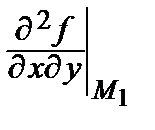= 8 ∙ (–4) + 24 = –8, С ₁= 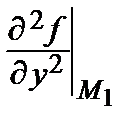= 2;

Δ₁ = А ₁ С ₁ – В ₁² = –64 => точка М ₁(4; 0) не является точкой экстремума;

б) М ₂(–2; 0): А ₂ = 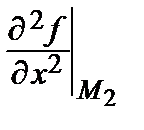= 8 ∙ 0 = 0, В ₂ = 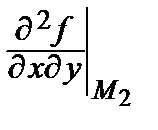= 8 ∙ (–2) + 24 = 8, С ₂= 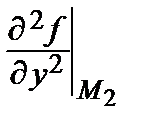= 2;

Δ₂ = А ₂ С ₂ – В ₂² = –64 => точка М ₂(–2; 0) не является точкой экстремума;

в) М ₃(–3; 2): А ₃ = 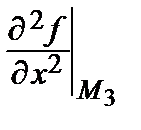= 8 ∙ 2 = 16, В ₃ = 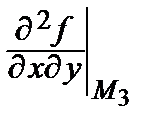= 8 ∙ (–3) + 24 = 0, С ₃ = 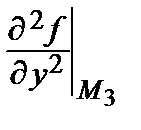= 2;

Δ₃ = А ₃ С ₃ – В ₃² = 32 => точка М ₃(–3; 2) является точкой экстремума, т.к. А ₃ > 0, то это точка

локального минимума функции, значение которой в этой точке f _min = f (–3, 2) = –10.

Пример 2. Исследовать на экстремум функцию z (x, y), заданную неявно уравнением 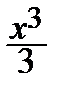+ 2 у ² – z ² x + z = 0.

Решение. Схема исследования обычная, но необходимо учитывать неявное задание функции.

1. Необходимые условия. Положим F (x, y, z) = 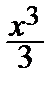+ 2 у ² – z ² x + z

<=> => .

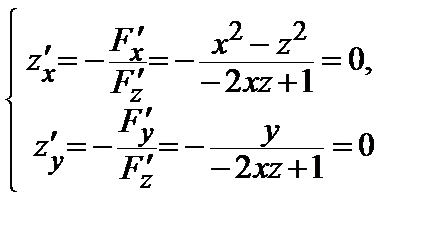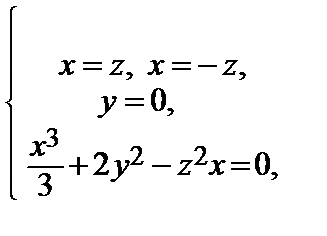К третьей системе присоединили уравнение, определяющее нашу неявную функцию.

Условия у = 0 и z = x приводят исходное уравнение к виду 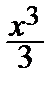– х ³ + x = 0, корни которого

x = 0, x = ± , .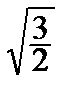

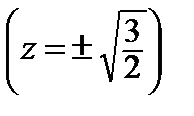Условия у = 0 и z = – x приводят исходное уравнение к виду 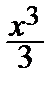– х ³ – x = 0, имеющему один действительный корень x = 0. Получаем три пары (x = 0; у = 0), , .

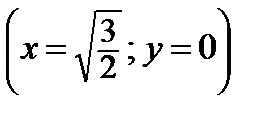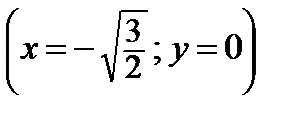Если x = 0, у = 0, то и z = 0, а, значит, и f_x ¢ = 0. Это означает, что в окрестности точки (0; 0) уравнение не определяет однозначную функцию, и эта точка не подлежит исследованию. Остаются две стационарные точки: М ₁ 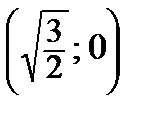и М ₂ .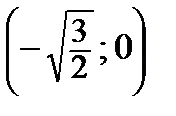

2. Найдем вторые производные по правилам дифференцирования неявных функций:

= = ;

= = ; = = – .

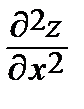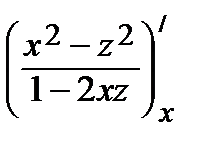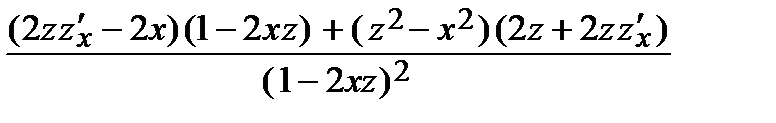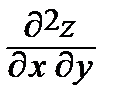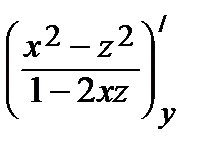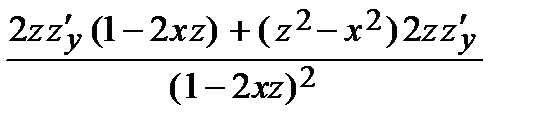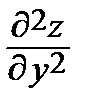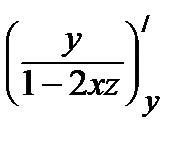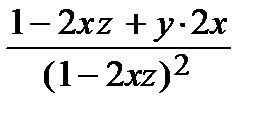С учетом того, что у = 0, z = х, z_x ¢ = z_y 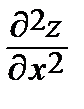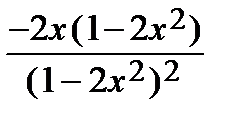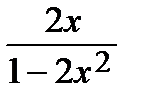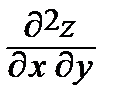¢ = 0,

= = – , = 0, = – .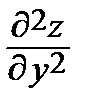

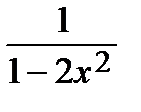3. Проверяем точки на достаточность условий экстремума.

а) М ₁ 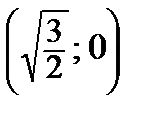: А ₁= 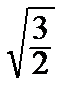, В ₁= 0, С ₁= 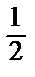; Δ₁ = А ₁ С ₁ – В ₁² > 0, A ₁ > 0 => точка М ₁ – точка минимума;

б) М ₂ 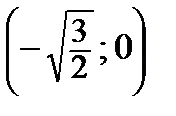: А ₂ = – 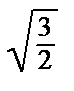, В ₂ = 0, С ₂= 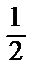= 2; Δ₂ = А ₂ С ₂ – В ₂² < 0, A ₂ > 0 => экстремума нет.

Значение экстремума z = x = 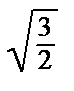= z _min.

Пример 3. Исследовать на экстремум функцию z= x ⁴ + у ⁴.

Решение. 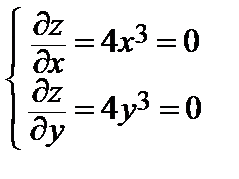=> x = 0, y = 0 => M (0; 0) – стационарная точка.

А = 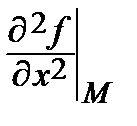= 0, В = 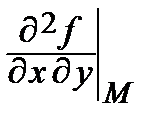= 0, С = 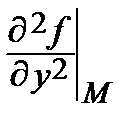= 0 => Δ = АС – В ² = 0 => достаточные условия не дают ответа о наличии или отсутствии экстремума. Поступаем так: рассматриваем ближайшую окрестность точки М. Имеем: во всех точках, отличных от M (0; 0), z (x, y) > z (0; 0). Следовательно,

M (0; 0) – точка минимума.

Пример 4. Исследовать на экстремум функцию z= x ⁴ + у ⁴.

Решение. Эта функция в точке M (0; 0) экстремума не имеет, т.к. в любой

окрестности этой точки найдутся как точки, в которых z (x, y) > z (0; 0), так и

точки, в которых z (x, y) < z (0; 0) – функция растет по х и убывает по у. Это

говорит о том, что M (0; 0) – точка минимакса («седловая» точка функции z).

Под условным экстремумом понимается поиск экстремума некоторой функции z = f (x, y) при условии, что точки (x; y) удовлетворяют еще некоторым условиям, например, уравнению φ ( x, y ) = 0, называемом уравнением связи.

F (x, y, λ) = f (x, y) + λ φ (x, y),

которая называется функцией Лагранжа, а λ – множителем Лагранжа.

Чтобы найти точки, которые могут быть точками условного экстремума функции z = f (x, y) при условии связи φ (x, y) = 0:

1) составляем функцию Лагранжа F (x, y, λ) = f (x, y) + λ φ (x, y),

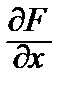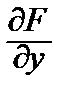2) приравнивая нулю производные и этой функции и присоединяя к полученным уравнениям уравнение связи, получим систему из 3-х уравнений:

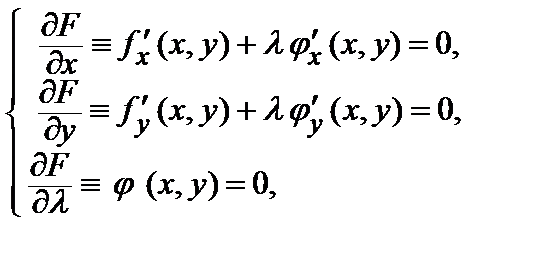
из которых находим значения λ и координаты х, у возможных точек экстремума.

Вопрос о существовании и характере условного экстремума решается

1) на основании изучения знака второго дифференциала функции Лагранжа:

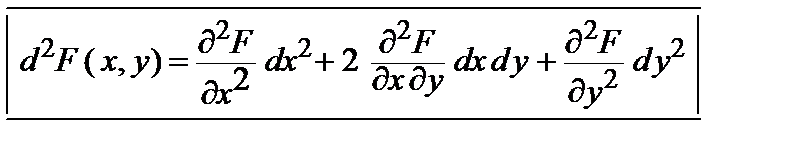
если в стационарной точке d ² F > 0 (d ² F < 0), то эта точка является точкой условного минимума (максимума).

2) на основании изучения знаков определителя D (x ₀, y ₀) = 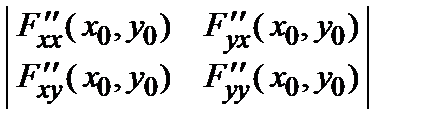и производно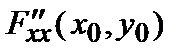й (или ).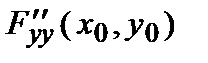

Если D (x ₀, y ₀) > 0, то в точке (x ₀, y ₀) функция f (x, y) имеет условный минимум, если 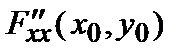> 0

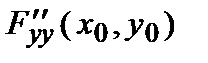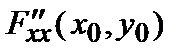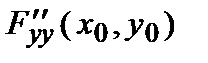( > 0) и условный максимум, если < 0 ( < 0).

Пример 1. Найти наибольшее значения функции z = xу, если переменные х и у

связаны соотношением 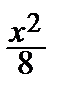+ 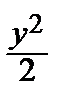– 1 = 0.

Решение. Строим функцию Лагранжа F (x, y, λ) = f (x, y) + λ φ (x, y) = ху + λ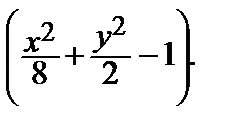

Находим стационарные точки этой функции 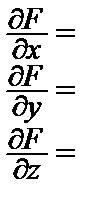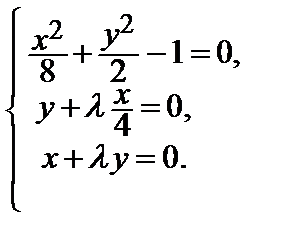Т. к. ищется наибольшее значение функции, то x > 0 и у > 0. С учетом этого решение системы имеет вид: х = 2, у = 1, λ = – 2. Т.о., имеется одна стационарная точка М (2; 1; – 2). Чтобы выяснить характер условного экстремума в этой точке. Найдем второй дифференциал функции Лагранжа при λ = – 2 (d ² z = d (dz) = 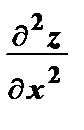dx ² + 2 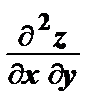dx dy + 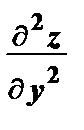dy ²):

d ² F = – 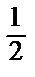dx ² + 2 dxdy – 2 dy ².

Из уравнения связи находим: dy (2; 1) = – 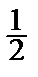dx. Следовательно,

d ² F (2; 1) = – 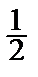dx ² + 2 dx 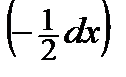– 2 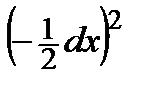= – 2 dx ² < 0,

поэтому точка (2; 1) является точкой условного максимума функции z = xу. При этом z _max = z (2; 1) = 2.

Этот результат легко проверить, если найти обычный экстремум функции z = x :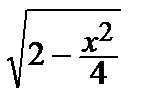

z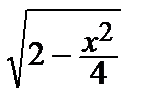_x ¢ = + x ∙ 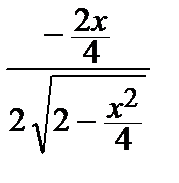= 0 <=> 2 – 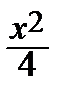= =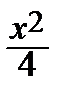> x ² = 4 => x = 2 => y = 1.

Т.к. z_x ¢ = 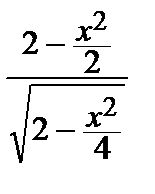при переходе через точку x = 2 меняет знак с «+» на «–»,

то x = 2 – точка максимума и z _max = z (2; 1) = 2.

Пример 2. Найти экстремум функции z = x ² + y ² (параболоид вращения) при условии х + у = 1.

Решение. (Метод Лагранжа) Функция Лагранжа в данном случае имеет вид:

F (x, y;l) = x ² + y ² + l (х + у – 1).

Для отыскания стационарных точек составляем систему:

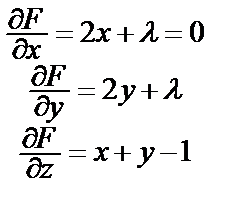=> x = y = 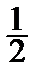, λ = –1 F (x, y;l) = x ² + y ² – х – у + 1.

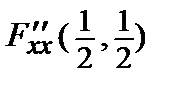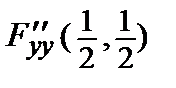Для нее: = 2; = 2; 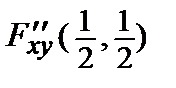= 0 =>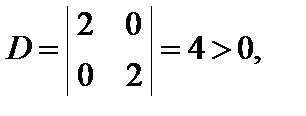 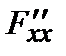= 2 > 0.

Т.о., точка (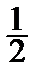, 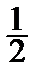) является точкой условного минимума функции z = x ² + y ² при условии х + у = 1.

Date: 2015-08-06; view: 3622; Нарушение авторских прав