
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Образец выполнения контрольной
|
|
1. Производная по направлению. Градиент
Пусть z = f (x, y) – дифференцируемая в некоторой области D функция и точка М 0(x 0, y 0)Î D. Пусть l – некоторое направление (вектор с началом в точке М 0), а е = {cos a, sin a } - орт этого направления. Пусть
М (x 0+D х, y 0+D у) – точка в направлении l от точки М 0.
Производная функции f (x, y) по направлению l:
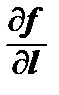 =
= 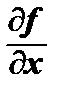 cos a +
cos a + 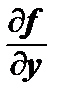 sin a.
sin a.
Производная по направлению для функции 3 -х переменных u = f (x, y, z):
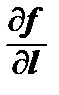 =
= 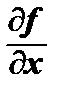 cos a +
cos a + 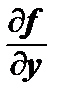 cos β +
cos β + 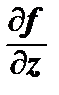 cos γ,
cos γ,
где e = {cos a, cos β, cos γ } – орт направленияl (cos a, cos β, cos γ – направляющие косинусы направления l).
Градиентом функции z = f (x, y) (скалярного поля) называется вектор с координатами 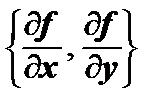 ,
,
определенный на плоскости Оху.
Обозначение: 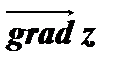 =
= 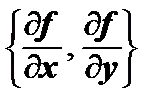 .
.
Имеет место равенство 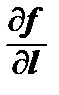 = (grad z, e), т.е. производная по направлению l равна скалярному произведению векторов градиента и орта направления l.
= (grad z, e), т.е. производная по направлению l равна скалярному произведению векторов градиента и орта направления l.
Вектор grad z в каждой точке направлен по нормали к линии уровня, проходящей через данную точку в сторону возрастания функции. При этом
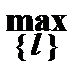
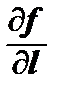 =
= 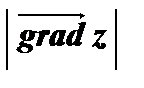 =
= 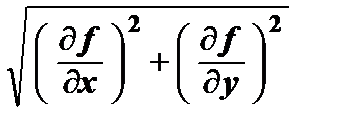 .
.
Скорость изменения функции f по некоторому направлению l равна проекции вектора градиента на это направление:
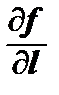 = pr l
= pr l 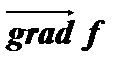 =
= 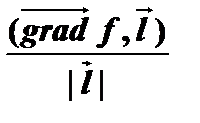 .
.
Градиентом функции u = f (x, y, z) называется вектор с координатами 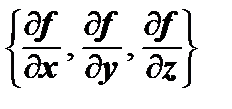 , определенный в трехмерном пространстве Охуz.
, определенный в трехмерном пространстве Охуz.
Пример 1. Найти производную функции z = f (x, y) = 3 x 2 – 5 y 2 в точке А (1; – 1)
по направлению к точке В (2; 1).
Решение. Вектор АВ = l = { 2 – 1, 1 – (– 1)} = {1, 2}; ½ l ½= 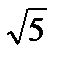 Þ cos a = 1 /
Þ cos a = 1 / 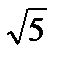 ;
;
sin a = 2 / 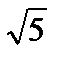 => е = {1 /
=> е = {1 / 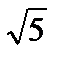 , 2 /
, 2 / 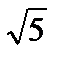 } (орт направления l).
} (орт направления l).
Далее zx ¢ = 6 x; zy ¢ = – 10 y; zx ¢½ A = 6; zy ¢½ A = 10.
=> 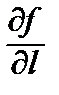 ½ A = 6 × (1 /
½ A = 6 × (1 / 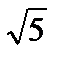 ) + 10 × (2 /
) + 10 × (2 / 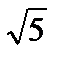 ) = 26 /
) = 26 / 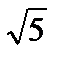 .
.
Пример 2. Даны: функция z = x 2 + 3 y 3– ху, точка А (1; 1), вектор а = { – 5, 12}.
Найти grad z ½ A и 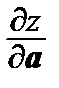 ½ A.
½ A.
Решение. zx ¢ = 2 x – у; zy ¢ = 9 y 2– х; zx ¢½ A = 1; zy ¢½ A = 8 => grad z ½ A = {1, 8} = i + 8 j.
½ а ½= 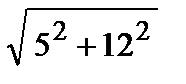 =
= 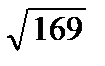 = 13 => cos a = – 5 / 13; sin a = 12 / 13 =>
= 13 => cos a = – 5 / 13; sin a = 12 / 13 =>
(¶ z / ¶ а)½ A = 1× (– 5 / 13) + 8× (12 / 13) = 91/ 13.
Максимальная производная в точке А (1; 1) равна
½ grad z (1; 1)½ = 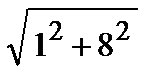 =
= 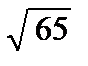 , а по направлению а величина производной
, а по направлению а величина производной
равна 91/ 13.
2. Вторые частные производные
Если задана функция z = f (х, y) и вычислены ее частные производные
f ′x = 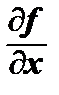 и f ′у =
и f ′у = 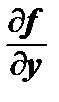 , то они могут быть также дифференцируемыми функциями двух переменных х и у.
, то они могут быть также дифференцируемыми функциями двух переменных х и у.
Принятые обозначения:
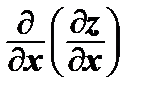 =
= 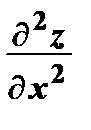 – вторая частная производная по х;
– вторая частная производная по х;
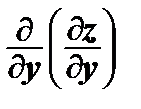 =
= 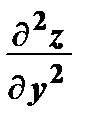 – вторая частная производная по у;
– вторая частная производная по у;
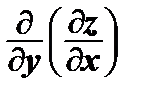 =
= 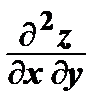 и
и 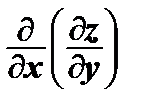 =
= 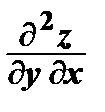 – смешанные частные производные второго порядка.
– смешанные частные производные второго порядка.
Date: 2015-08-06; view: 509; Нарушение авторских прав