Неоднородные системы

Неоднородной системой линейных уравнений называется система вида: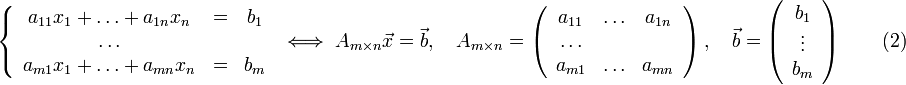

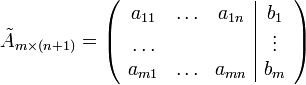её расширенная матрица.

Теорема (об общем решении неоднородных систем).

Пусть r= rangA=rangA (т.е. система (2) совместна), тогда:

Если r=n, где n- число переменных системы(2), то решение (2) существует и оно единственно;

Если r<n, то общее решение системы (2) имеет вид 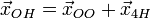— общее решение системы (1), называемое общим однородным решением 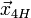частное решение системы (2), называемое частным неоднородным решением.

Пример:

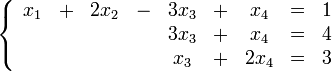
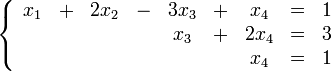
Тогда переменные х4=1 и х3=1обязательно будут главными, возьмём также х2 в качестве главной.

Заметим, что 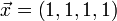является частным решением.

Составим однородную систему: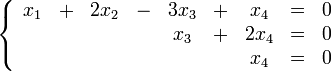

тогда, подставив единицу в качестве свободной переменной х1, получим ФСР однородной системы:

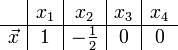
Общее решение системы может быть записано так:

Date: 2015-08-06; view: 262; Нарушение авторских прав