
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Пример: периодическая последовательность прямоугольных импульсов
|
|
Пример: периодическая последовательность прямоугольных импульсов с амплитудой Е, длительностью 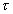 и периодом Т (рис.5). Отношение
и периодом Т (рис.5). Отношение 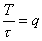 называется скважностью последовательности. Такой сигнал не удовлетворяет условиям для функций, к которым применимо разложение в обобщенный ряд Фурье. Однако существующие реальные сигналы, близкие по форме к прямоугольным импульсам, удовлетворяют этим условиям. Поэтому для простоты можно заменить реальные почти прямоугольные импульсы идеализированными прямоугольными, хотя ряд Фурье для них плохо сходится в углах.
называется скважностью последовательности. Такой сигнал не удовлетворяет условиям для функций, к которым применимо разложение в обобщенный ряд Фурье. Однако существующие реальные сигналы, близкие по форме к прямоугольным импульсам, удовлетворяют этим условиям. Поэтому для простоты можно заменить реальные почти прямоугольные импульсы идеализированными прямоугольными, хотя ряд Фурье для них плохо сходится в углах.
Итак, пусть 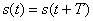 , причем в течение периода
, причем в течение периода 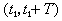 сигнал можно описать выражением:
сигнал можно описать выражением:
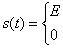 при
при 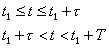
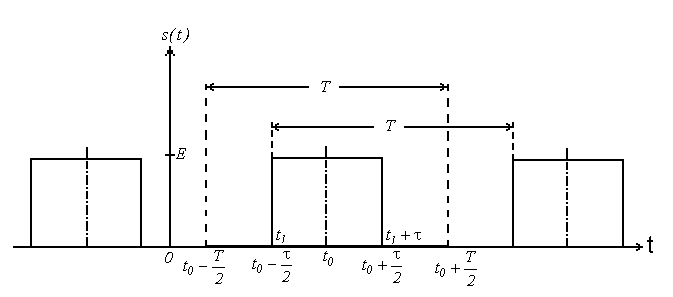
Рис. 5
Для упрощения вывода формулы для коэффициентов ряда Фурье, выберем такой интервал интегрирования, на котором сигнал, отличный от нуля расположен симметрично. Обозначим через t0 время, соответствующее середине импульса на одном из периодов (лучше ближайшем к началу отсчета). Тогда 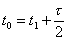 и на периоде
и на периоде 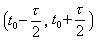 имеем
имеем
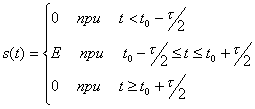 .
.
Тогда коэффициенты тригонометрического ряда Фурье определятся следующим образом:
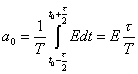 ;
;

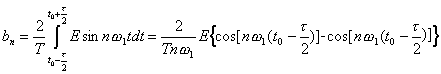
Проведя преобразования, получим:
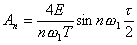 ;
;
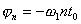 .
.
Аналогичные результаты гораздо проще получить с помощью коэффициентов для комплексного ряда Фурье. Действительно,
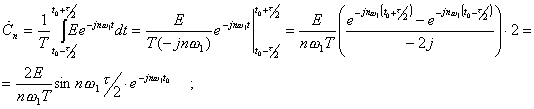
т.к. An=2Cn, то 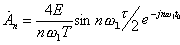 .
.
Соотношения для An легко привести к виду, удобному для построения АЧС, помножив и разделив его на 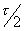 , получим:
, получим:
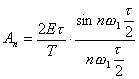 .
.
Учитывая, что 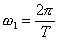 , можно получить и следующее выражение:
, можно получить и следующее выражение:
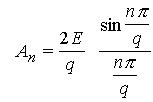 .
.
Так для q=2 («меандр») получаем следующие значения для амплитуд и фаз составляющих спектра:
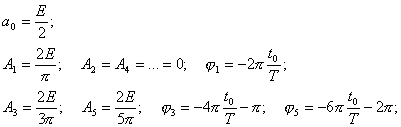
и т.д.
(добавление величины 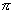 обусловлено переходом синуса через нуль).
обусловлено переходом синуса через нуль).
Таким образом, спектр меандра имеет вид рис. 6:
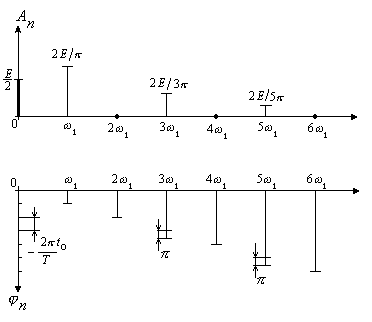
Рис. 6
Часто изменение знака синуса отражают на амплитудно-частотном спектре, показывая как бы отрицательное значение амплитуды. Тогда АЧС и ФЧС выглядят следующим образом (рис. 7):
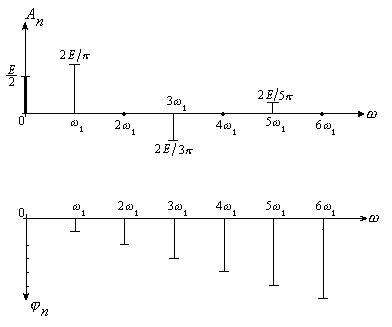
Рис. 7
Если сигнал задан так, что t 0 = 0, то все 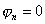 , и можно ограничиться только графиком АЧС с «отрицательными» амплитудами.
, и можно ограничиться только графиком АЧС с «отрицательными» амплитудами.
При увеличении скважности за счет, например, увеличения периода при неизменном 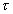 , амплитуды составляющих уменьшаются, расстояние между ними также уменьшается.
, амплитуды составляющих уменьшаются, расстояние между ними также уменьшается.
При произвольных значениях q и t 0 удобнее воспользоваться построением огибающих АЧХ и ФЧХ. Заменим 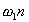 на текущее значение частоты
на текущее значение частоты 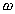 . Получим
. Получим
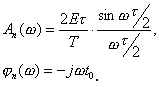
Построим график 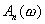 . Из соотношения для An видим, что огибающая меняет знак и, следовательно, проходит через нуль в точках, где
. Из соотношения для An видим, что огибающая меняет знак и, следовательно, проходит через нуль в точках, где 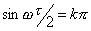 , откуда определяем частоты прохождения огибающей АЧХ через нуль:
, откуда определяем частоты прохождения огибающей АЧХ через нуль:
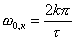 , где к= 1, 2, 3, …
, где к= 1, 2, 3, …
Частота, соответствующая k= 1, называется первым нулем спектра. Если 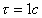 , то частота первого нуля равна
, то частота первого нуля равна 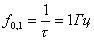 , а если
, а если 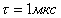 , то
, то 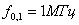 . Следующие нули огибающей спектра кратны этой величине. На частоте
. Следующие нули огибающей спектра кратны этой величине. На частоте 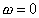 огибающая имеет максимум равный
огибающая имеет максимум равный
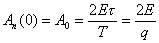 ,
,
откуда постоянная составляющая
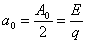 .
.
Следующий максимум будет на частоте 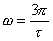 .
.
Величина огибающей на этой частоте равна
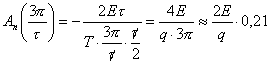 ;
;
то есть второй максимум примерно в 5 раз ниже максимума на нулевой частоте. Следующие максимумы уменьшаются пропорционально частоте.
Огибающая ФЧХ линейна и зависит от величины запаздывания 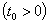 или опережения
или опережения 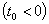 середины импульса относительно t= 0, т.е.
середины импульса относительно t= 0, т.е.  .
.
Таким образом, графики огибающих можно нарисовать так, как пунктиром показано на рис.8.
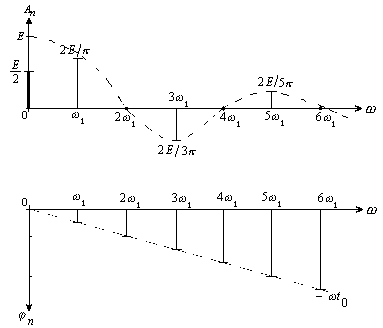
Рис. 8
Для построения самого спектра (АЧС и ФЧС) достаточно на частотах, кратных 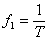 , провести отрезки до пересечения с огибающей. Для меандра (q= 2) в каждом лепестке огибающей (между нулями) будет лишь по одной ненулевой составляющей на частотах:
, провести отрезки до пересечения с огибающей. Для меандра (q= 2) в каждом лепестке огибающей (между нулями) будет лишь по одной ненулевой составляющей на частотах: 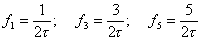 и т.д. Постоянная составляющая
и т.д. Постоянная составляющая 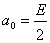 . Все четные гармоники имеют в этом случае нулевые амплитуды. Можно амплитудный спектр построить без учета знака синуса во втором, четвертом и т.д. лепестках, в этом случае на этих частотах к
. Все четные гармоники имеют в этом случае нулевые амплитуды. Можно амплитудный спектр построить без учета знака синуса во втором, четвертом и т.д. лепестках, в этом случае на этих частотах к 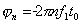 следует добавить
следует добавить 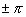 .
.
| <== предыдущая | | | следующая ==> |
| Природа оже-електронів | | | Теоретичні відомості. Тема: Спостереження спектрів випромінювання |
Date: 2015-08-06; view: 599; Нарушение авторских прав