
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Определение главного фокусного расстояния собирающей линзы по величине его изображения
|
|
1.Расположение приборов остается таким же, что и в первом случае.
2.На экране Э находят сильно увеличенное изображение предмета 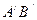 .
.
3.Измеряют величину предмета АВ, изображения 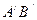 и расстояние от изображения предмета до линзы f.
и расстояние от изображения предмета до линзы f.
4.Из формул 1.1 и 1.2 после преобразования получается следующее выражение для вычисления фокусного расстояния 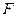 :
:
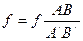 . (1.3)
. (1.3)
5.Меняя положение экрана и линзы, измеряют величины АВ, 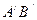 и f три раза.
и f три раза.
6.Подставляя значения АВ, 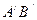 и f в формулу (1.3) вычисляют
и f в формулу (1.3) вычисляют 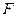 .
.
Полученные результаты заносят в таблицу.
| Номер опыта | F | АВ | 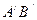
| 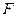
| 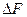
|
Упражнение 2
ОПРЕДЕЛЕНИЕ ГЛАВНОГО ФОКУСНОГО РАССТОЯНИЯ РАССЕИВАЮЩЕЙ ЛИНЗЫ
Оборудование: оптическая скамья, собирающая линза, рассеивающая линза, осветитель, экран.
Порядок выполнения работы
 Вогнутая, или рассеивающая линза дает мнимое изображение. Фокусное расстояние вогнутой линзы определяют следующим образом:
Вогнутая, или рассеивающая линза дает мнимое изображение. Фокусное расстояние вогнутой линзы определяют следующим образом:
1. Собирают схему, как в первом случае для выпуклой линзы.
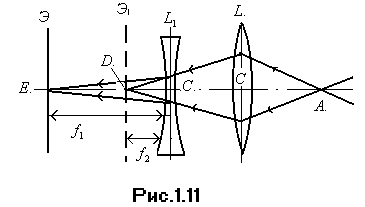
2. Замечают точку D, положение экрана, когда получается резкое изображение предмета, (рис.1.11).
3. Между собирающей линзой L и точкой D помещают рассеивающую линзу L1. Опять добиваются резкого изображения предмета на экране, которое из D перейдет в точку Е. Для линзы L1 "предметом" является изображение в точке D, даваемое линзой L от предмета А.
Пользуясь обратимостью хода лучей в системах линз, можно рассматривать эти лучи света как распространяющиеся из точки Е. Тогда точка D будет мнимым изображением точки Е (после преломления лучей в линзе L1).
Следовательно, расстояние 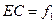 и
и 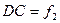 . Найдем эти расстояния (не менее трех раз).
. Найдем эти расстояния (не менее трех раз).
4. Найденные значения 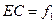 и
и 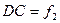 подставляют в формулу (1.1). Принимая во внимание, что
подставляют в формулу (1.1). Принимая во внимание, что 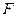 и
и 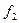 имеют в данном случае отрицательный знак, получим:
имеют в данном случае отрицательный знак, получим: 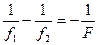 , откуда.
, откуда. 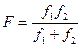 .
.
Упражнение 3
НАБЛЮДЕНИЕ СФЕРИЧЕСКОЙ И ХРОМАТИЧЕСКОЙ АБЕРРАЦИЙ ЛИНЗЫ
Оборудование: оптическая скамья, двояковыпуклая линза, экран, две диафрагмы (круглая и кольцевая), набор светофильтров.
а) Наблюдение сферической аберрации
Порядок выполнения работы
1. Между источником К и линзой L помещают круглую диафрагму, которая выделяет пучок лучей, проходящих через центр линзы, и, получив резкое изображение предмета (см.упр.1), отмечают расстояние от экрана до линзы 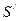 .
.
2.Между источником К и линзой L помещают кольцевую диафрагму, которая выделяет пучок лучей, проходящих через края линзы. Получив резкое изображение предмета, отмечают положение экрана и измеряют расстояние от линзы до экрана 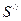 .
.
Разность 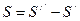 и есть величина сферической аберрации.
и есть величина сферической аберрации.
3. Измерения проделать три раза и занести в таблицу.
| Номер опыта | 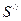
| 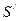
| 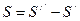
| 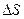
| 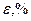
|
4. Ответ представить в виде: S = 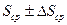
б) Наблюдение за хроматической аберрацией линз.
 |
Порядок выполнения работы
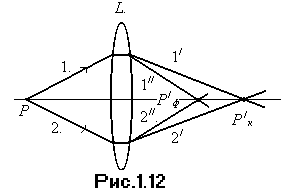
1. Между источником и линзой помещают фиолетовый светофильтр и получают резкое изображение предмета на экране (точка 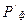 (рис 1.12)).
(рис 1.12)).
2. Отмечают положение экрана 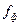 и рассчитывают фокусное расстояние
и рассчитывают фокусное расстояние 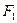 по формуле (1.1).
по формуле (1.1). 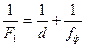
3. Между источником и линзой помещают красный светофильтр и получают резкое изображение предмета на экране (точка 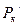 ).
).
4. Отмечают положение экрана 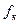 и рассчитывают фокусное расстояние по формуле:
и рассчитывают фокусное расстояние по формуле: 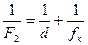 .
.
5. Вычисляют величины: Δf = f k – f ф и ΔF = Fk - Fф , которые характеризуют величину хроматической аберрации
Контрольные вопросы
1. Построить изображения в положительных и отрицательных линзах, когда предмет находится между: оптическим центром и главным фокусом, главным и двойным фокусом, за двойным фокусом и в фокусе линзы.
2. Какие параметры и характеристики линз вы знаете?
3. Как определить оптическую силу системы линз?
4. В чем заключаются причины сферической аберрации? Какие способы их устранения вы знаете?
5. Какова роль диафрагм в оптических приборах?
6. Какое физическое явление вызывает хроматическую аберрацию? Какими способами удается ее уменьшить?
ЛАБОРАТОРНАЯ РАБОТА №2
ИЗМЕРЕНИЕ АБСОЛЮТНОГО ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ ТВЕРДЫХ И ЖИДКИХ ВЕЩЕСТВ
Вопросы допуска
1. Относительный и абсолютный показатели преломления и их физический смысл.
2. Как определяется абсолютный показатель преломления твердых тел с помощью микроскопа?
3. Как определить абсолютный показатель преломления жидкостей с помощью рефрактометра?
Упражнение 1
ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ ПЛОСКОПАРАЛЛЕЛЬНОЙ СТЕКЛЯННОЙ ПЛАСТИНКИ С ПОМОЩЬЮ МИКРОСКОПА
Оборудование: набор стеклянных пластин, микроскоп типа МБУ-4, микрометр.
Содержание и метод выполнения работы
При прохождении света через ровную и плоскую границу двух прозрачных веществ неодинаковой оптической плотности падающий луч света АО разделяется на два луча: отраженный луч ОВ и преломленный луч ОD (рис.1.12). Направления этих лучей определяется следующими законами отражения и преломления света:
1. 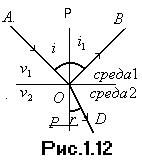 Луч АО, падающий на преломляющую поверхность, нормаль к поверхности в точке падения РОР, луч отраженный ОВ и луч преломленный ОD лежат в одной плоскости.
Луч АО, падающий на преломляющую поверхность, нормаль к поверхности в точке падения РОР, луч отраженный ОВ и луч преломленный ОD лежат в одной плоскости.
2. Угол отражения РОВ численно равен углу падения РОА.
3. Синус угла падения 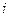 относится к синусу угла преломления
относится к синусу угла преломления 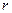 , как скорость света в первой среде
, как скорость света в первой среде 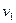 относится к скорости света во второй среде
относится к скорости света во второй среде 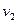 :
: 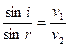 .(1.4)
.(1.4)
Этот закон гласит о том, что свет распространяется в различных средах с различной скоростью.
Для двух данных сред и для луча данной длины волны отношение скорости света в среде 1 к скорости света в среде 2 или отношение синуса угла падения к синусу угла преломления есть величина постоянная: 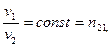
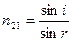 .
.
Величина 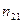 называется относительным коэффициентом преломления второй среды по отношению к первой.
называется относительным коэффициентом преломления второй среды по отношению к первой.
Показатель преломления 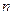 данной среды по отношению к вакууму называется абсолютным коэффициентом преломления.
данной среды по отношению к вакууму называется абсолютным коэффициентом преломления.
Абсолютный коэффициент преломления среды 2 (рис1.12):
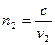 ,
, 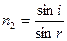 , где
, где 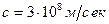 -скорость света в вакууме,
-скорость света в вакууме, 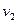 -скорость света в данной среде 2, т.е. показатель (коэффициент) преломления среды есть отношение скорости света в вакууме к скорости света в данной среде.
-скорость света в данной среде 2, т.е. показатель (коэффициент) преломления среды есть отношение скорости света в вакууме к скорости света в данной среде.
 В основе метода, определения показателя преломления стекла при помощи микроскопа, лежит явление кажущегося уменьшения толщины стеклянной пластинки вследствие преломления световых лучей, проходящих в стекле при рассматривании пластинки нормально к ее поверхности.
В основе метода, определения показателя преломления стекла при помощи микроскопа, лежит явление кажущегося уменьшения толщины стеклянной пластинки вследствие преломления световых лучей, проходящих в стекле при рассматривании пластинки нормально к ее поверхности.
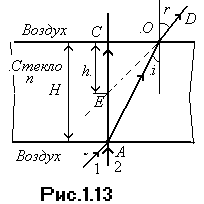
В точку А, находящуюся на нижней поверхности стеклянной пластинки (рис.1.13), падают два луча света 1 и 2. Луч 2 падает на пластинку нормально к ее поверхности и поэтому проходит сквозь пластинку и выходит в воздух в точке С, не испытывая преломления. Луч 1 преломляется и выходит из пластинки в точку О в направлении D.
При выходе из пластинки луч ОD образует угол преломления 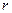 -больший, чем угол падения
-больший, чем угол падения 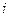 . Если смотреть из точки D по направлению DО, то наблюдатель будет видеть точку пересечения лучей ОD и АС не в точке А, а в точке Е, т.е. толщина пластинки будет казаться равной СЕ.
. Если смотреть из точки D по направлению DО, то наблюдатель будет видеть точку пересечения лучей ОD и АС не в точке А, а в точке Е, т.е. толщина пластинки будет казаться равной СЕ.
Из рисунка видно, что кажущаяся толщина пластинки 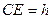 меньше действительной ее толщины
меньше действительной ее толщины 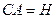 .
.
Для лучей, близких к нормально падающим лучам, углы падения и преломления малы. В этом случае синусы можно заменить тангенсами и по закону преломления света (рассматривая обратный ход лучей): 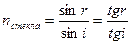 .
.
В нашем случае, после соответствующих преобразований имеем: 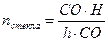 или
или 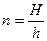 .
.
Следовательно, показатель преломления стекла можно найти из отношения истинной толщины стеклянной пластинки к кажущейся ее толщине.
Порядок выполнения работы
1. Измеряют микрометром истинную толщину стеклянной пластинки 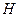 в том месте, где нанесены штрихи, и берут ее значение в миллиметрах.
в том месте, где нанесены штрихи, и берут ее значение в миллиметрах.
2. Определяют кажущуюся толщину стеклянной пластинки 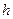 , для чего пластинку кладут на столик микроскопа под объектив так, чтобы оба штриха пересекали оптическую ось прибора.
, для чего пластинку кладут на столик микроскопа под объектив так, чтобы оба штриха пересекали оптическую ось прибора.
3. Двигая тубус микроскопа, добиваются четкого изображения видимого в микроскоп штриха, нанесенного на верхнюю поверхность пластинки. Записывают отсчет микрометрического винта и считают его за нулевое деление (от этого нулевого деления производят дальнейшие отчеты).
4. Опускают тубус микроскопа до получения четкого изображения штриха на нижней поверхности пластинки. Новый отсчет микрометрического винта показывает кажущуюся толщину пластинки: 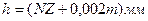 , где
, где 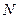 -число полных оборотов барабана винта,
-число полных оборотов барабана винта, 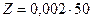 - шаг винта, 50 -число делении в одном полном обороте барабана, 0,002 - цена одного деления барабана винта,
- шаг винта, 50 -число делении в одном полном обороте барабана, 0,002 - цена одного деления барабана винта, 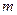 - число делении в неполном обороте барабана. Как видно, за один полный оборот барабана микрометрического винта тубус микроскопа перемещается на
- число делении в неполном обороте барабана. Как видно, за один полный оборот барабана микрометрического винта тубус микроскопа перемещается на 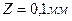 .
.
5. Вычисляют показатель преломления стекла по формуле: 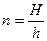 . Измерения проводят не менее трех раз. Полученные результаты заносят в таблицу.
. Измерения проводят не менее трех раз. Полученные результаты заносят в таблицу.
| № п/п | H мм | N | m | 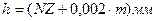
| n | 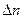
| 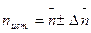
|
Упражнение 2
ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ ЖИДКОСТЕЙ ПРИЗМЕННЫМ РЕФРАКТОМЕТРОМ
Оборудование: рефрактометр типа ИРФ-22, исследуемые жидкости, промокательная бумага.
Содержание и метод выполнения работы
Определение показателя преломления жидкостей и растворов при помощи призменного рефрактометра основана на использовании явления, обратного явлению полного внутреннего отражения света.
На приборе можно исследовать вещества, показатель преломления которых меньше показателя преломления измерительной призмы.
 |
Основной частью рефрактометра являются две призмы
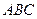 и
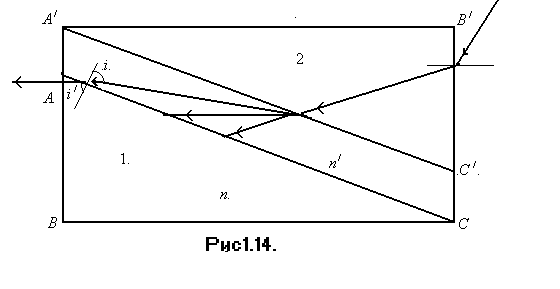
и 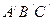 (рис.1.14), изготовленные из стекла сорта флинтгласа с большим показателем преломления. Между этими призмами помещают несколько капель исследуемой жидкости.
(рис.1.14), изготовленные из стекла сорта флинтгласа с большим показателем преломления. Между этими призмами помещают несколько капель исследуемой жидкости.
Призма 1 с хорошо отполированной гранью 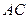 является измерительной, а призма 2 с матовой гранью
является измерительной, а призма 2 с матовой гранью 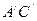 -осветительной.
-осветительной.
Рассмотрим ход лучей в призмах. От источника света лучи падают на грань 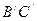 , преломляются и падают на матовую поверхность
, преломляются и падают на матовую поверхность 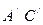 . Вследствие рассеивания матовой поверхностью в исследуемую жидкость входят лучи различных направлений. Проходя слой жидкости, лучи попадают на грань
. Вследствие рассеивания матовой поверхностью в исследуемую жидкость входят лучи различных направлений. Проходя слой жидкости, лучи попадают на грань 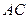 призмы 1. Т.к. показатель преломления жидкости
призмы 1. Т.к. показатель преломления жидкости 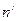 меньше показателя преломления измерительной призмы
меньше показателя преломления измерительной призмы 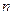 , то лучи всех направлений, преломляясь на границе жидкость-стекло, входят в призму 1.
, то лучи всех направлений, преломляясь на границе жидкость-стекло, входят в призму 1.
Применяя закон преломления, запишем: 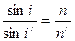 , или
, или 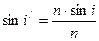 .(1.5)
.(1.5)
Из (1.5) видно, что с увеличением угла 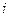 угол
угол 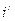 также увеличится, достигая максимального значения при угле падения
также увеличится, достигая максимального значения при угле падения 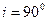 , то есть, когда падающий луч скользит по поверхности
, то есть, когда падающий луч скользит по поверхности 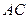 .
.
 Здесь имеет место явление, обратное явлению полного внутреннего отражения. Так как зазор между призмами 1 и 2 очень мал, то приближенно можно считать, что лучи с наибольшим углом падения являются скользящими.
Здесь имеет место явление, обратное явлению полного внутреннего отражения. Так как зазор между призмами 1 и 2 очень мал, то приближенно можно считать, что лучи с наибольшим углом падения являются скользящими.
Тогда, считая 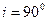 , можно написать:
, можно написать: 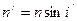 .
.
Таким образом, зная 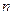 и угол преломления
и угол преломления 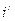 , можно вычислить
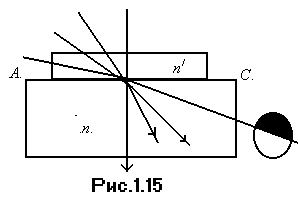
, можно вычислить 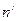 . Если на пути лучей, выходящих из призмы, поставить зрительную трубу, то нижняя часть ее поля зрения будет освещена, а верхняя - останется темной. Получающаяся граница света и тени определяется лучом, выходящим из призмы под предельным углом, как показана на рисунке (1.15).
. Если на пути лучей, выходящих из призмы, поставить зрительную трубу, то нижняя часть ее поля зрения будет освещена, а верхняя - останется темной. Получающаяся граница света и тени определяется лучом, выходящим из призмы под предельным углом, как показана на рисунке (1.15).
Скользящий луч по границе АС будет определять границу освещенной и темной частей поля зрения.
Порядок выполнения работы
1. Установку шкалы прибора производят по эталонному образцу с известным показателем преломления.
2. Для измерения показателя преломления той или иной жидкости: откидывают верхнюю часть измерительной головки прибора, пипеткой наносят несколько капель исследуемой жидкости на поверхность измерительной призмы, осторожно закидывают головку прибора, наблюдая в окуляр зрительной трубы и вращая маховиком измерительную головку, находят границу раздела с перекрестием нитей окуляра и снимают отсчет по шкале показателей преломления. Индексом для отсчета служит неподвижный, горизонтальный штрих шкалы. Целые, десятые, сотые и тысячные значения показателя преломления отсчитываются по шкале, десятитысячные–оцениваются на глаз.
3. Опыт провести с водой, глицерином и сахарными растворами. Полученные результаты занести в таблицу.***
| № | жидкость | n | 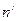
| 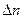
| 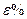
|
Сравнить полученные результаты со справочными данными. Сделать выводы.
4. Построить график зависимости показателя преломления сахарного раствора от концентрации сахара.
5. По графику определить неизвестную концентрацию.
Контрольные вопросы
1. Сформулировать законы отражения и преломления света.
2. Объяснить явление полного внутреннего отражения. Как используется обратное явление для измерения показателя преломления в рефрактометрах?
3. Что характеризует абсолютный показатель преломления? От каких параметров вещества может зависеть абсолютный показатель преломления?
4. Показатели преломления воды, стекла и алмаза равны соответственно 1,33, 1,5, 2,42. В каком из этих трех веществ угол преломления максимален, если угол падения во всех трех случаях одинаков?
II. ИНТЕРФЕРЕНЦИЯ СВЕТА
Рассмотрим две волны одинаковой циклической частоты 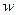 , распространяющиеся в одном направлении. Накладываясь, друг на друга, они возбуждают в некоторых точках пространства колебания одинакового направления:
, распространяющиеся в одном направлении. Накладываясь, друг на друга, они возбуждают в некоторых точках пространства колебания одинакового направления:
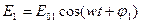 ,
,
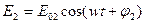 .
.
Амплитуда результирующего колебания в данной точке определяется, формулой: 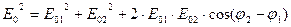 .
.
Если разность фаз 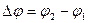 возбуждаемых колебаний остается постоянной по времени, то волны называются когерентными, а источники таких волн – когерентными источниками. В случае некогерентных волн
возбуждаемых колебаний остается постоянной по времени, то волны называются когерентными, а источники таких волн – когерентными источниками. В случае некогерентных волн 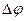 непрерывно изменяется, принимая с равной вероятностью любые значения, вследствие чего среднее по времени значение:
непрерывно изменяется, принимая с равной вероятностью любые значения, вследствие чего среднее по времени значение: 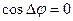 и
и 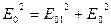 .
.
Так как интенсивность света 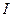 ~
~ 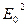 , то интенсивность, наблюдаемая при наложении некогерентных волн, равна сумме интенсивностей, создаваемых каждой волной в отдельности:
, то интенсивность, наблюдаемая при наложении некогерентных волн, равна сумме интенсивностей, создаваемых каждой волной в отдельности: 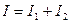 .
.
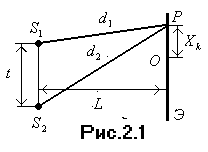 В случае когерентных волн
В случае когерентных волн 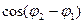 имеет постоянное во времени, но разное для каждой точки пространства значение, так что интенсивность:
имеет постоянное во времени, но разное для каждой точки пространства значение, так что интенсивность: 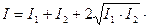
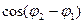 , (2.1) так же постоянна для каждой точки пространства.
, (2.1) так же постоянна для каждой точки пространства.
Интенсивность света по всему полю, где происходит наложение когерентных волн, будет изменяться, причем в тех точках пространства, для которых 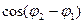 >
> 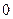 значения
значения 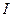 >
> 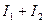 , в тех точках, для которых
, в тех точках, для которых 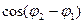 <
< 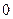 ,
, 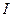 <
< 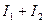 . Таким образом, при наложении когерентных световых волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают устойчивые максимумы, в других минимумы интенсивности. Это явление называется интерференцией световых волн.
. Таким образом, при наложении когерентных световых волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают устойчивые максимумы, в других минимумы интенсивности. Это явление называется интерференцией световых волн.
Особенно отчетливое проявление интерференции света наблюдается в том случае, когда интенсивность интерферирующих волн одинакова: 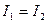 . Согласно (2.1) в этом случае:
. Согласно (2.1) в этом случае:
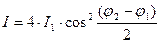 (2.2), в минимумах
(2.2), в минимумах 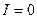 , в максимумах
, в максимумах 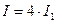 . Для некогерентных волн при этом же условии получается всюду одинаковая интенсивность
. Для некогерентных волн при этом же условии получается всюду одинаковая интенсивность 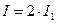 .
.
Пусть 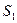 и
и 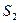 (рис. 2.1) – когерентные источники. Расстояние между источниками
(рис. 2.1) – когерентные источники. Расстояние между источниками 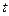 мало по сравнению с расстоянием
мало по сравнению с расстоянием 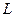 до экрана Э, помещенного параллельно линии, соединяющей источники. Характер интерференционной картины на экране зависит от разности фаз
до экрана Э, помещенного параллельно линии, соединяющей источники. Характер интерференционной картины на экране зависит от разности фаз 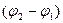 , которую интерферирующие волны имеют в точке наблюдения
, которую интерферирующие волны имеют в точке наблюдения 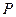 . Эта разность фаз, в свою очередь, обусловлена тем, что волны от источников
. Эта разность фаз, в свою очередь, обусловлена тем, что волны от источников 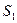 и
и 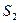 до точки
до точки 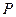 проходят разные пути
проходят разные пути 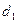 и
и 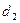 . Разность путей
. Разность путей 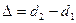 (разность хода лучей) связана с разностью фаз
(разность хода лучей) связана с разностью фаз 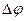 , соотношением:
, соотношением:
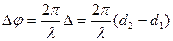 . (2.3)
. (2.3)
Теперь (2.2) с учетом (2.3) можно записать в виде:
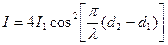 .
.
Интенсивность в точке 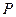 будет максимальна
будет максимальна 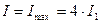 , если выполняется условие:
, если выполняется условие: 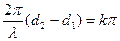 , или
, или 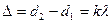 , (2.4), где
, (2.4), где 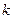 – целое число.
– целое число.
Интенсивность в точке 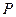 будет минимальна
будет минимальна 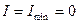 , если
, если 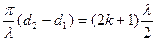 , или
, или 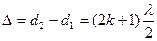 (2.5).
(2.5).
Условия (2.4) и (2.5) называются условиями интерференционного максимума и минимума соответственно.
В точке 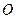 будет находиться центральная светлая полоса (разность хода равна 0). Расстояние от центра до
будет находиться центральная светлая полоса (разность хода равна 0). Расстояние от центра до 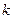 -ой светлой полосы
-ой светлой полосы 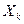 опреВеляется из условия:
опреВеляется из условия: 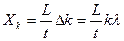 .
.
Положение темных полос определяется условием: 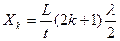 .
.
Ширина интерференционной полосы или расстояние между соседними светлыми (темными) полосами ΔХ есть: 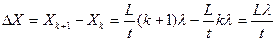 , откуда
, откуда 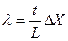 . (2.6)
. (2.6)
|
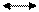
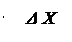 |  |
ЛАБОРАТОРНАЯ РАБОТА №3
ОПРЕДЕЛЕНИЕ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ МЕТОДОМ ЮНГА
Вопросы допуска
1. Дайте определение явлению интерференции.
2. Какие волны называются когерентными?
3. Как осуществляется интерференция в методе Юнга?
4. Как определяется длина световой волны в данной лабораторной работе?
Оборудование: оптическая скамья, лазер, экран, столик для установки пластины с двойной щелью, собирающая линза, набор стеклянных светофильтров.
Содержание и метод выполнения работы
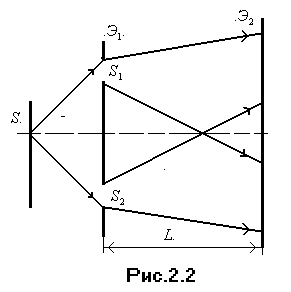 Из точки S (рис.2.2) распространяется монохроматическая световая волна, которая падает на два очень малых и близко расположенных на расстоянии t друг от друга отверстия
Из точки S (рис.2.2) распространяется монохроматическая световая волна, которая падает на два очень малых и близко расположенных на расстоянии t друг от друга отверстия 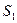 и
и 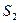 в пластине
в пластине 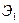 . По принципу Гюйгенса эти два отверстия являются самостоятельными источниками световых колебаний; из этих источников будут выходить когерентные волны, т.е. происходит дифракция на узких щелях,
. По принципу Гюйгенса эти два отверстия являются самостоятельными источниками световых колебаний; из этих источников будут выходить когерентные волны, т.е. происходит дифракция на узких щелях, 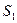 и
и 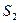 , параллельных
, параллельных 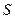 , которые прорезаны в непрозрачной пластинке
, которые прорезаны в непрозрачной пластинке 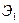 . За пластинкой происходит интерференция налагающихся когерентных волн, источниками которых являются щели
. За пластинкой происходит интерференция налагающихся когерентных волн, источниками которых являются щели 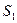 и
и 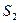 .
.
При известных расстояниях 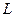 от когерентных источников
от когерентных источников 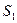 и
и 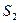 до экрана Э2 и
до экрана Э2 и 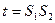 – между источниками по формуле (2.6) можно определить длину световой волны
– между источниками по формуле (2.6) можно определить длину световой волны 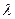 , измерив ширину интерференционной полосы
, измерив ширину интерференционной полосы 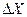 .
.
Порядок выполнения работы
1. Устанавливают пластинку с двойной щелью на расстоянии 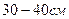 от лазера, включают его. Перемещая пластину с двойной щелью перпендикулярно оптической скамье, выводят интерференционные полосы на экран. Двигая пластинку с двойной щелью, добиваются того, чтобы полосы интерференции были яркими и четкими.
от лазера, включают его. Перемещая пластину с двойной щелью перпендикулярно оптической скамье, выводят интерференционные полосы на экран. Двигая пластинку с двойной щелью, добиваются того, чтобы полосы интерференции были яркими и четкими.
2. Измеряют расстояние между темными и светлыми полосами (ширину интерференционной полосы) 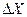 . Для обеспечения большей точности определения
. Для обеспечения большей точности определения 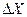 необходимо измерить расстояние между удаленными, но хорошо видимыми полосами и разделить его на число световых полос
необходимо измерить расстояние между удаленными, но хорошо видимыми полосами и разделить его на число световых полос 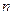 .
.
3. Далее измеряют расстояние 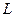 от пластинки с двойной щелью до экрана и по формуле (2.6) определяют
от пластинки с двойной щелью до экрана и по формуле (2.6) определяют 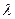 . Расстояние между источниками
. Расстояние между источниками 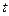 указано на пластинке с двойной щелью.
указано на пластинке с двойной щелью.
4. Повторите опыт, изменив расстояние 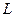 от пластинки с двойной щелью до экрана. Сделайте вывод, как зависит расстояние между темными и светлыми полосами
от пластинки с двойной щелью до экрана. Сделайте вывод, как зависит расстояние между темными и светлыми полосами 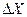 от
от 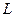 расстояния от пластинки с двойной щелью до экрана.
расстояния от пластинки с двойной щелью до экрана.
4. Установите вместо пластинки с известным расстоянием между щелями 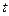 другую пластинку с неизвестным
другую пластинку с неизвестным 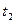 и по формуле (2.6) вычисляем его. Длину волны
и по формуле (2.6) вычисляем его. Длину волны 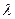 берем из предыдущего упражнения.
берем из предыдущего упражнения.
5. Полученные данные занесите в таблицу.
| Номер опыта | t | L | ΔX | λ | Δλ |
Контрольные вопросы
1. В чем заключаются особенности сложения когерентных и некогерентных волн?
2.Поясните понятие разности хода и разности фаз. Как выражается связь между ними?
3. Назовите условия усиления и ослабления света при интерференции.
4. Выведите выражение для ширины полос интерференции 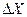 .
.
III. ДИФРАКЦИЯ СВЕТА
Наблюдения свидетельствовали о нарушении прямолинейности распространения света в некоторых условиях. Так, если пропустить свет через щель, то при достаточной ее ширине края щели очерчены вполне резко. Если же щель сужать, то сначала изображение так же сужается без искажений, но затем края делаются размытыми, при дальнейшем уменьшении ширины щели ее изображение заметно расширяется. В подобных наблюдениях проявляется «загибание» световых лучей названное дифракцией.
Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле – любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Благодаря дифракции волны могут попадать в область геометрической тени, огибать препятствия, проникать через небольшие отверстия в экранах и т.д. Например, звук хорошо слышен за углом дома, т.е. звуковая волна его огибает.
Явление дифракции объясняется с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн. Огибающая этих волн задает положение волнового фронта в следующей момент времени.
Пусть плоская волна нормально падает на отверстие в непрозрачном экране. Согласно принципу Гюйгенса, каждая точка выделяемого отверстием волнового фронта служит источником вторичных волн. Построив огибающую вторичных волн для некоторого момента времени видим, что фронт волны заходит в область геометрической тени, т.е. волна, огибает края отверстия.
Явление дифракции характерно для волновых процессов. Поэтому если свет является волновым процессом, то для него должна наблюдаться дифракция, значит световая волна, падающего на границу какого-либо непрозрачного тела, должна огибать его. Но опыт показывает, что предметы, освещаемые светом, идущим от точечного источника, дают резкую тень и, следовательно, лучи не отклоняются от их прямолинейного распространения. Почему же возникает резкая тень, если свет имеет волновую природу? К сожалению, теория Гюйгенса ответить на этот вопрос не могла.
Принцип Гюйгенса решает только задачу о направлении распространения волнового фронта, но не затрагивает вопроса об амплитуде, а следовательно, и об интенсивности волн, распространяющихся по разным направлениям. Френель вложил в принцип Гюйгенса физический смысл. Дополнив его идеей интерференции вторичных волн.
Согласно принципу Гюйгенса–Френеля, световая волна, возбуждаемая каким-либо источником 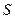 , может быть представлена как результат суперпозиции когерентных вторичных волн, "излучаемых" фиктивными источниками. Такими источниками могут служить бесконечно малые элементы любой замкнутой поверхности, охватывающей источник
, может быть представлена как результат суперпозиции когерентных вторичных волн, "излучаемых" фиктивными источниками. Такими источниками могут служить бесконечно малые элементы любой замкнутой поверхности, охватывающей источник 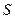 . Обычно в качестве этой поверхности выбирают одну из волновых поверхностей, поэтому все фиктивные источники действуют синфазно. Таким образом, волны, распространяющиеся от источника, являются результатом интерференции всех когерентных вторичных волн.
. Обычно в качестве этой поверхности выбирают одну из волновых поверхностей, поэтому все фиктивные источники действуют синфазно. Таким образом, волны, распространяющиеся от источника, являются результатом интерференции всех когерентных вторичных волн.
Учет амплитуд и фаз вторичных волн позволяет в каждом конкретном случае найти амплитуду (интенсивность) результирующей волны в любой точке пространства, т.е. определить закономерности распространения света.
Немецкий физик Фраунгофер рассмотрел дифракцию плоских световых волн, или дифракцию в параллельных лучах. Дифракция Фраунгофера, имеющая большое практическое значение, наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызывавшего дифракцию. Чтобы осуществить такую дифракцию, достаточно точечный источник света поместить в фокусе собирающей линзы, а дифракционную картину исследовать в фокальной плоскости второй собирающей линзы, установленной за препятствием.
Большое практическое значение имеет дифракция, наблюдаемая при прохождении света через дифракционную решетку – систему параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками.
 Дифракционная картина на решетке является результатом взаимной интерференции волн, идущих от всех щелей, т.е. в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей.
Дифракционная картина на решетке является результатом взаимной интерференции волн, идущих от всех щелей, т.е. в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей.
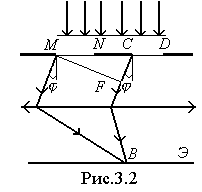
Рассмотрим дифракционную решетку. На рисунке 3.2. для наглядности показаны только две соседние щели 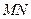 и
и 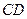 . Если ширина каждой щели равна
. Если ширина каждой щели равна 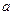 , а ширина непрозрачных участков между щелями
, а ширина непрозрачных участков между щелями 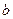 , то величина
, то величина 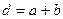 называется постоянной (периодом) дифракционной решетки.
называется постоянной (периодом) дифракционной решетки.
Пусть плоская монохроматическая волна падает нормально к плоскости решетки. Так как щели находятся друг от друга на одинаковых расстояниях, то разность хода лучей, идущих от двух соседних щелей, будут для данного направления 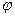 одинаковы в пределах всей дифракционной решетки:
одинаковы в пределах всей дифракционной решетки:
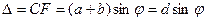 (3.1)
(3.1)
Очевидно. что в направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, т.е. главные минимумы интенсивности будут наблюдаться в направлениях, определяемых условием:
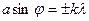
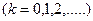 (3.2)
(3.2)
Кроме того вследствие взаимной интерференции световых лучей, посылаемых двумя щелями, в некоторых направлениях они будут гасить друг друга, т.е. возникнут дополнительные минимумы. Очевидно, эти дополнительные минимумы будут наблюдаться в тех направлениях, которым соответствует разность хода лучей 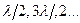 , посылаемых, например, от крайних левых точек
, посылаемых, например, от крайних левых точек 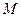 и
и 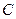 обеих щелей. Таким образом, условие дополнительных минимумов:
обеих щелей. Таким образом, условие дополнительных минимумов:
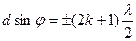
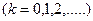 .
.
Наоборот, действие одной щели будет усиливать действие другой, если:
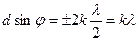
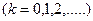 (3.3)
(3.3)
т.е. выражение (3.3) задает условие главных максимумов дифракционной решетки.
Таким образом, полная дифракционная картина для двух щелей определяется из условий:
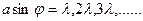 –главные минимумы,
–главные минимумы,
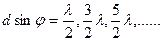 –дополнительные минимумы,
–дополнительные минимумы,
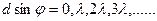 –главные максимумы.
–главные максимумы.
Если дифракционная решетка состоит из 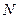 щелей, то условием главных минимумов является условие (3.2), условием главных максимумов–условие (3.3), а условием дополнительных минимумов:
щелей, то условием главных минимумов является условие (3.2), условием главных максимумов–условие (3.3), а условием дополнительных минимумов:
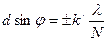
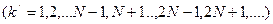 (3.4)
(3.4)
где 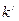 может принимать все целочисленные значения, кроме
может принимать все целочисленные значения, кроме 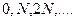 .Следовательно, в случае
.Следовательно, в случае 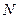 щелей между двумя главными максимумами располагается
щелей между двумя главными максимумами располагается 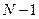 дополнительных минимумов.
дополнительных минимумов.
Основными характеристиками дифракционной решетки являютсяее дисперсия, разрешающая способность и область дисперсии.
Дисперсия. Угловая дисперсия определяется угловым расстоянием между двумя спектральными линиями, отличающимися на 1 нм. Если двум близким спектральным линиям 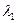 и
и 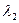 , отличающимся на
, отличающимся на 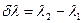 , соответствует угловое расстояние
, соответствует угловое расстояние 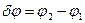 ,то мерой угловой дисперсии является отношение:
,то мерой угловой дисперсии является отношение: 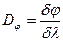 , (3.5)
, (3.5)
Для дифракционной решетки под 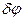 , следует понимать угловое расстояние в спектре одного и того же порядка между дифракционными максимумами для двух спектральных линий с отличающимися на
, следует понимать угловое расстояние в спектре одного и того же порядка между дифракционными максимумами для двух спектральных линий с отличающимися на 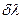 длинами волн. Дифференцируя, получим:
длинами волн. Дифференцируя, получим: 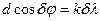 , откуда:
, откуда:
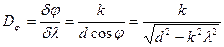 (3.6).
(3.6).
Как видно, угловая дисперсия возрастает с увеличением порядка спектра. Дисперсия может также определяться линейным расстоянием 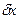 на экране между спектральными линиями с
на экране между спектральными линиями с 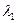 и
и 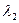 , отличающимися на
, отличающимися на 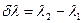 :
:
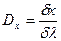 (3.7).
(3.7).
Определенная таким образом дисперсия называется линейной, она связана с угловой дисперсией соотношением: 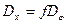 .
.
Разрешающая способность. Переход от максимума данной волны к минимуму происходит более или менее плавно. Если в спектре присутствуют две близкие спектральные линии, то возможность их раздельного восприятия на данном спектральном приборе определяется не только положением их максимумов, но и тем, как быстро происходит спад интенсивностей от максимума к минимуму, или, иначе говоря, возможность разрешения спектральных линий зависит от их ширины.
В качестве меры разрешающей способности спектрального прибора принимается отношение длины волны, вблизи которой производится наблюдение, к той минимальной разности длин волн 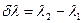 ,, которая может быть разрешенана этом приборе:
,, которая может быть разрешенана этом приборе:
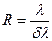 .
.
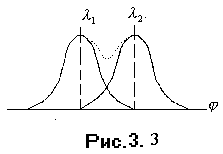 Согласно критерию Релея, разрешение двух близких спектральных линий одинаковой интенсивности считается полным, когда расстояние между максимумами этих линий равно или больше расстояния от максимума одной из линий до ее первого минимума (рис. 3.3).
Согласно критерию Релея, разрешение двух близких спектральных линий одинаковой интенсивности считается полным, когда расстояние между максимумами этих линий равно или больше расстояния от максимума одной из линий до ее первого минимума (рис. 3.3).
На рис. 3.3 пунктирная линия - результат сложения интенсивностей в линиях с длинами 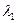 и
и 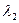 / Линии в спектре видны раздельно.
/ Линии в спектре видны раздельно.
В спектре порядка К положение максимума для волны длиной 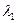 :
:
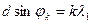 (3.8)
(3.8)
Условие первого минимума в том же порядке для длины волны 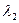 :
: 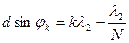 .
.
По Релею эти максимумы и минимумы видны под одним и тем же углом,
т.е.: 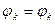 ,
,
или 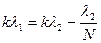 ,
,
откуда: 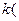
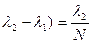 .
.
Положим 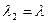 , тогда:
, тогда: 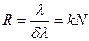 .
.
Итак, разрешающая способность дифракционной решетки определяется произведением порядка спектра на общее число ее штрихов. Чем меньше 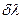 вблизи
вблизи 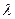 , тем более близкие линии можно будет наблюдать раздельно в дифракционном спектре.
, тем более близкие линии можно будет наблюдать раздельно в дифракционном спектре.
Область дисперсии. В реальных условиях работы прибора мы имеем дело не с монохроматическим светом и не с набором близких монохроматических линий, а с некоторым спектральным интервалом конечной ширины 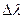 , простирающимся от
, простирающимся от 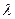 до
до 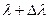 . Благодаря этому в спектрах высоких порядков происходит наложение максимумов разных волн в различных порядках. Предельная ширина
. Благодаря этому в спектрах высоких порядков происходит наложение максимумов разных волн в различных порядках. Предельная ширина 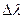 спектрального интервала, при которой наложение спектров еще не происходит, называется областью дисперсии.
спектрального интервала, при которой наложение спектров еще не происходит, называется областью дисперсии.
Для дифракционной решетки направление 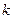 -го максимума для света с длиной волны
-го максимума для света с длиной волны 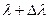 определяется условием:
определяется условием:
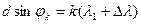 , (3.9)
, (3.9)
максимум же порядка 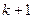 для волны с длиной
для волны с длиной 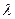 :
: 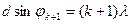 .(3.10)
.(3.10)
Поскольку наложение спектров 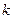 -го и
-го и 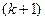 -го порядков начинается при условии
-го порядков начинается при условии 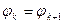 , то из (3.9) и (3.10) легко найти, что:
, то из (3.9) и (3.10) легко найти, что:
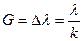
Как видим, область дисперсии сужается с увеличением порядка спектра.
Date: 2015-08-06; view: 897; Нарушение авторских прав