
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дифракционная решетка как спектральный прибор
|
|
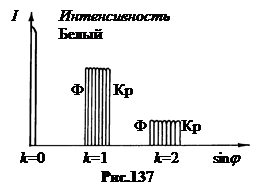
1. Дифракционный спектр. Если на дифракционную решетку падает не монохроматический свет, то дифракционные максимумы для лучей разных длин волн пространственно расходятся. Нулевой максимум для всех длин волн при j = 0 совпадает, а максимумы других порядков для фиолетовых лучей располагаются ближе к центру, чем для красных (рис.137). Между ними располагаются максимумы промежуточных цветов. В результате формируются дифракционные спектры. Если k = 1, говорят, спектр первого порядка, при k = 2 - спектр 2 - го порядка и так далее. Между спектрами расположены практически - темные зоны очень слабых побочных максимумов.
 Максимальное количество наблюдаемых дифракционных спектров находится из условия:
Максимальное количество наблюдаемых дифракционных спектров находится из условия: 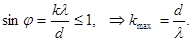 (16.1)
(16.1)
У решеток с числом щелей 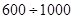 на один миллиметр наблюдается практически лишь один спектр первого порядка. Действительно даже при d = 1 ç 600 мм k max » 2. Но спектр второго порядка находится далеко от центрального максимума и имеет очень малую интенсивность. При d ≤ 1 ç 1000 мм k max< 2.
на один миллиметр наблюдается практически лишь один спектр первого порядка. Действительно даже при d = 1 ç 600 мм k max » 2. Но спектр второго порядка находится далеко от центрального максимума и имеет очень малую интенсивность. При d ≤ 1 ç 1000 мм k max< 2.
Способность решетки разлагать белый свет в спектр позволяет использовать ее как спектральный прибор. Основными характеристиками дифракционной решетки как спектрального прибора являются дисперсия и разрешающая способность.
2. Угловая дисперсия D j определяет степень угловой растянутости спектра в зависимости от длины волны, 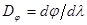 . Величина ее найдется дифференцированием по l условия главных максимумов.
. Величина ее найдется дифференцированием по l условия главных максимумов. 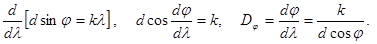 (16.2)
(16.2)
Угловая дисперсия решетки зависит от единственного параметра решетки - ее периода d. Зависимость от k не имеет практического значения, потому что в спектральных приборах используют исключительно k = 1. Выразив cos j из условия главного максимума, 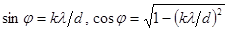 , получаем выражение для угловой дисперсии:
, получаем выражение для угловой дисперсии:
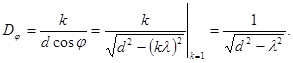 (16.3)
(16.3)
Из формулы хорошо видно, что угловая дисперсия быстро увеличивается по мере приближения d к l. При 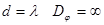 , но этот результат не имеет смысла, так как
, но этот результат не имеет смысла, так как 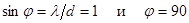 °. Направление главного максимума решетки уходит из пределов наблюдения.
°. Направление главного максимума решетки уходит из пределов наблюдения.
3. Линейная дисперсия D l численно равна расстоянию между одноименными максимумами для двух волн, длины l которых отличаются на единицу.
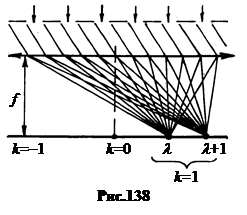 В спектральных приборах ее величина определяются произведением угловой дисперсии решетки на фокусное расстояние объектива f (рис.138).
В спектральных приборах ее величина определяются произведением угловой дисперсии решетки на фокусное расстояние объектива f (рис.138). 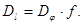 (16.4)
(16.4)
Чем меньше постоянная решетки d, тем на больший угол расходятся одноименные максимумы. На величину дисперсии не влияет общее число щелей N.
Решетка с периодом d = 2 мкм (500 щелей на миллиметр) имеет угловую дисперсию для зеленых лучей Dj = 5,2∙105 р/м. Спектральный прибор с объективом f = 0,5 м и данной решеткой имеет линейную дисперсию в зеленых лучах Dl = Dj ∙ f = 5,2∙105∙0,5 = 2,6∙105 м/м.
В системе единиц СИ численные значения Dl и Dj следует рассматривать как формальные характеристики спектральных приборов, поскольку ни один прибор не обеспечивает возможность наблюдения спектра с длинами волн 1 м. Таких величин много в физике, например, модуль Юнга твердых тел и др.
4. Разрешающая способность определяет возможность разрешения, то есть раздельного восприятия двух близких одно-порядковых максимумов, получающихся для разных длин волн. 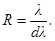 (16.5)
(16.5)
Для дифракционной решетки Рэлей предложил следующий критерий спектрального разрешения. Спектральные линии с близкими длинами волн l и l + dl считаются разрешенными, если главный максимум дифракционной картины для одной длины волны l совпадает по своему положению с ближайшим дифракционным минимумом картины для другой длины волны 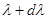 .
.
Найдем зависимость разрешающей способности R от параметров решетки.
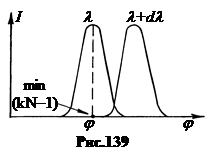 Пусть на угол j приходится k -тый главный максимум волны с длиной волны l, d sin j = ± kl. С увеличением длины волны главный максимум смещается в направлении увеличения угла j. При некотором значении длины волны l + dl на положение главного максимума волны l придется ближайший вторичный минимум волны l + dl, Nd sin j = (kN – 1)(l + dl). (рис.139). Получаем два уравнения. d sin j = kl. (16.6)
Пусть на угол j приходится k -тый главный максимум волны с длиной волны l, d sin j = ± kl. С увеличением длины волны главный максимум смещается в направлении увеличения угла j. При некотором значении длины волны l + dl на положение главного максимума волны l придется ближайший вторичный минимум волны l + dl, Nd sin j = (kN – 1)(l + dl). (рис.139). Получаем два уравнения. d sin j = kl. (16.6)
Nd sin j = (kN – 1)(l + dl), (16.7)
где k - порядок главного максимума, N - число щелей решетки.
Исключив из уравнений угол j, получаем:
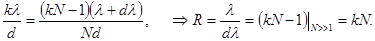 (16.8)
(16.8)
 Разрешение R пропорционально порядку k главного максимума и числу щелей решетки N. Первый путь повышения R не имеет практического значения, поскольку наблюдаются спектры исключительно первого порядка (k= 1). А вот повышение R за счет увеличения числа щелей N решетки на практике используется широко.
Разрешение R пропорционально порядку k главного максимума и числу щелей решетки N. Первый путь повышения R не имеет практического значения, поскольку наблюдаются спектры исключительно первого порядка (k= 1). А вот повышение R за счет увеличения числа щелей N решетки на практике используется широко.
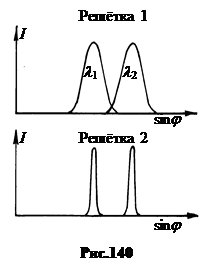
На рис.140 показаны однопорядковые максимумы, соответствующие длинам волн l 1 и l 2, наблюдающиеся в спектрах двух решеток. Обе решетки имеют одинаковый период d, поэтому их дисперсии одинаковы. То есть одинаково угловое расстояние между максимами l 1 и l 2. Но решетка 2 по сравнению с решеткой 1 имеет в два раза большее число щелей. Поэтому ее дифракционные максимумы более контрастны.
5. Историческая справка. Первые дифракционные решетки изготовил Йозеф Фраун-гофер в 1821г., наматывая тонкую проволоку на два параллельных винта. Эти решетки имели от 2 до 14 щелей на 1 мм. С их помощью Фраунгофер открыл темные линии в сплошном спектре Солнца (линии Фраунгофера), измерил длину волны l D -линий натрия (588,6 нм).
Для изготовления более совершенных решеток Фраунгофер перешел к нанесению штрихов на тонком золотом слое, покрывавшем стекло, а затем к нанесению алмазом непрозрачных штрихов непосредственно на стекле. Лучшая решетка Фраунгофера имела ширину 12,5 мм и период около 3 мкм (320 штрихов на один миллиметр).
В 1868 г. швед Андерс Ангстрём с помощью дифракционной решетки составил первый атлас солнечного спектра, в котором положение фраунгоферовых линий было измерено с точностью до 5 знаков.
В 1882 г. американец Генри Роуланд сконструировал и построил специальные машины для изготовления высококачественных решеток больших размеров. Решетки Роуланда имели до 800 линий на миллиметр и ширину до 10 сантиметров с общим числом щелей до 80000. Роуланд первый стал делать отражательные вогнутые решетки, выполняющие одновременно роль решетки и собирающей линзы.
 6. Амплитудные и фазовые дифракционные решетки. Решетки, представляющие собой систему прозрачных и непрозрачных параллельных полос, формируют вторичные лучи путем деления волнового фронта, вырезая из него с помощью прозрачных щелей отдельные участки. Амплитуда светового вектора волнового фронта делиться щелями на одинаковые амплитудные порции. Поэтому такие решетки называются амплитудными.
6. Амплитудные и фазовые дифракционные решетки. Решетки, представляющие собой систему прозрачных и непрозрачных параллельных полос, формируют вторичные лучи путем деления волнового фронта, вырезая из него с помощью прозрачных щелей отдельные участки. Амплитуда светового вектора волнового фронта делиться щелями на одинаковые амплитудные порции. Поэтому такие решетки называются амплитудными.
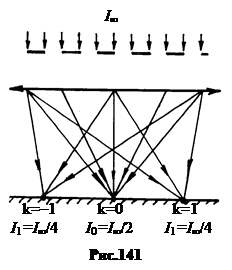
Главные недостатки амплитудной решетки в том, что примерно половина падающего на нее света задерживается непрозрачными участками, а половина прошедшей половины идет в направлении центрального максимума. В спектр первого порядка попадает не более 1 ç 4 падающего на решетку света (рис.141). Это снижает светосилу решетки как спектрального прибора и требует большой интенсивности пучков.
В 1910 г. Роберт Вуд сконструировал фазовую отражательную решетку. Особенность ее в том, что в ней практически нет непрозрачных участков, бесполезно задерживающих свет. Из-за сходства с лестницей такую решетку назвали э шелеттом (от фр. echelle-лестница).
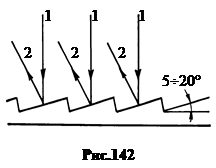 На зеркальной металлической поверхности выполнены борозды с косым треугольным профилем (рис.142). Параллельный пучок света направляется по нормали к решетке. Наибольшая часть энергии пучка 1 отражается по закону отражения в направлении 2. Угол наклона отражающих граней и постоянная решетки подбираются так, чтобы свет отражался в направлении спектра 1-го порядка. Тогда мощность излучения в нем оказывается много больше мощности излучения в спектрах всех остальных порядков. Практически решетка дает в этом случае только один спектр, собирая в нем до 80% энергии падающего на решетку света.
На зеркальной металлической поверхности выполнены борозды с косым треугольным профилем (рис.142). Параллельный пучок света направляется по нормали к решетке. Наибольшая часть энергии пучка 1 отражается по закону отражения в направлении 2. Угол наклона отражающих граней и постоянная решетки подбираются так, чтобы свет отражался в направлении спектра 1-го порядка. Тогда мощность излучения в нем оказывается много больше мощности излучения в спектрах всех остальных порядков. Практически решетка дает в этом случае только один спектр, собирая в нем до 80% энергии падающего на решетку света.
Оптическая промышленность развитых стран изготовляет в настоящее время эшеллеты с числом штрихов от 600 для видимой области и до 1 на миллиметр (для дальней ИК области). Размеры эшеллетов от 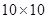 см2 до
см2 до 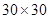 см2.
см2.
Гравированные решетки для исследования УФ лучей изготавливают в настоящее время с периодом до 3600 штрихов на миллиметр и размером до 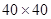 см2.
см2.
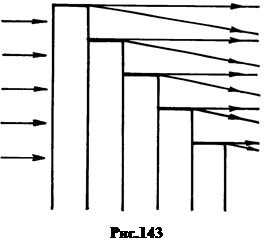 7. Эшелон Майкельсона является важной разновидностью дифракционной решетки как многолучевого интерферометра. Он был построен в 1898 г. и представляет собой стопу стеклянных высокооднородных пластин одинаковой толщины (±0,01 l), сложенных на оптический контакт так, что концы образуют лестницу со ступеньками равной толщины (рис.143).
7. Эшелон Майкельсона является важной разновидностью дифракционной решетки как многолучевого интерферометра. Он был построен в 1898 г. и представляет собой стопу стеклянных высокооднородных пластин одинаковой толщины (±0,01 l), сложенных на оптический контакт так, что концы образуют лестницу со ступеньками равной толщины (рис.143).
Параллельный пучок света, падая на эшелон, разделяется на несколько лучей по числу пластин, проходящих разные пути в материале пластины. В отличие от обыкновенной дифракционной решетки разность хода соседних лучей в эшелоне составляет десятки тысяч длин волн, а число этих лучей, равных числу пластин, обычно не превышает 30-40.
Благодаря тому, что прядок максимумов очень высок и достигает десятков тысяч 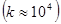 , эшелон Майкельсона обладает исключительно высокой разрешающей способностью,
, эшелон Майкельсона обладает исключительно высокой разрешающей способностью, 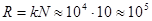 . Это высокое разрешение реализуется лишь в очень узком интервале длин волн. Поэтому эшелон Майкельсона пригоден для анализа очень узких участков спектра
. Это высокое разрешение реализуется лишь в очень узком интервале длин волн. Поэтому эшелон Майкельсона пригоден для анализа очень узких участков спектра 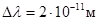 , в частности, для изучения мультиплетов спектральных линий.
, в частности, для изучения мультиплетов спектральных линий.
Обычно свет разлагается вначале в спектр приборами нормального разрешения, в основе которых лежит дифракционная решетка или призма (например, монохроматор УМ-2). А уже выведенный из прибора участок спектра расщепляется далее с помощью эшелона Майкельсона, интерферометра Фабри Перо или пластинки Люммера-Герке.
8. Голография (от греческого holjs – полный и grapho – пишу) метод безлинзового получения оптических изображений путем восстановления волнового фронта.
Процесс получения изображения в голографии включает в себя два этапа. На первом этапе изготавливается голограмма, то есть фотопластинка, с помощью которой можно восстановить световую волну, отраженную предметом. Не втором этапе с помощью голограммы восстанавливается световая волна и получается оптическое изображение предмета.
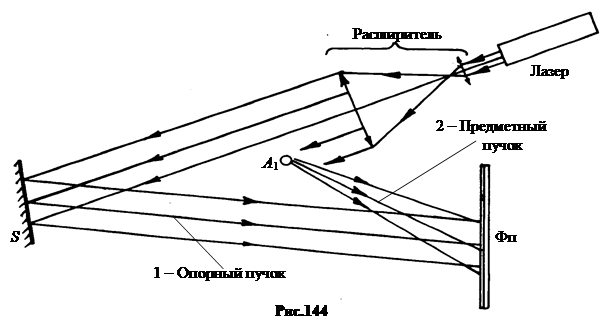 |
а. Получение голограммы. Пучок лучей от лазера, обладающий высокой пространственной и временной когерентностью, делится на две части. Одна часть отражается от плоского зеркала S, а другая направляется на предмет А1 (рис.144).
Отразившийся от зеркала опорный пучок 1 и отразившийся от предмета предметный пучок 2 (сигнальная волна), накладываясь друг на друга, создают интерференционную картину, которая фотографируется фотопленкой Фп. Проявленная и отфиксированная фотография называется голограммой. Голограмма в закодированной форме содержит полную информацию об амплитудах и фазах рассеянной предметом А1 волны. Под микроскопом она представляет собой сложную систему мелких почернений в слое прозрачной эмульсии. Поскольку разность хода между предметной и опорной волнами велика и может достигать нескольких метров, то столь же велика должна быть и пространственная когерентность интерферирующих пучков. Время когерентности должно доходить до 10–6¸10–5 с. Никакие источники, кроме лазеров, не могут обеспечить такие условия.
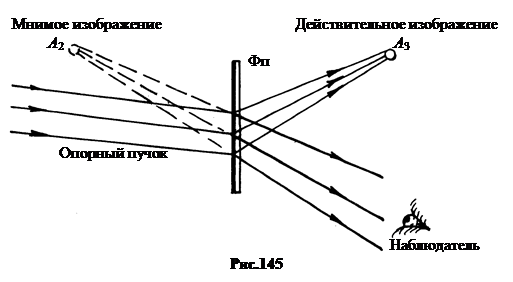 |
б. Восстановление волнового поля. Для этого на схеме рисунка 144 нужно убрать предмет А1 и осветить голограмму Фп одним опорным пучком. Взаимодействуя с голограммой (даже в негативе), опорный пучок создает в проходящих лучах дифракционную картину в виде двух изображений предмета А1 (рис.145).
В расходящихся лучах формируется мнимое изображение А2, расположенное там же, где был предмет А1. В сходящихся лучах формируется изображение А3, расположенное симметрично мнимому изображению А2. Плоскостью симметрии является голограмма Фп.
Голографическое изображение является объемным. Его зрительное восприятие ничем не отличается от восприятия предмета. Фотографируя мнимое изображение из разных точек, можно получить фотографии предмета в разных ракурсах.
На обычных фотографиях предмета судить о предмете можно лишь на основе площади всей фотографии. Если часть фотографии оторвать, то информация о предмете на оторванной части окажется утерянной. Оставшаяся часть фотографии не позволяет оптическими методами восстановить утерянную информацию.
Замечательным свойством голограммы является то, что каждый ее достаточно большой фрагмент содержит информацию обо всем предмете. При уменьшении фрагмента ухудшается лишь разрешающая способность изображения (контрастность). Поэтому информация, записанная в виде голограммы, имеет более высокую надежность хранения.
Date: 2015-08-06; view: 1656; Нарушение авторских прав