
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дифракция на щели
|
|
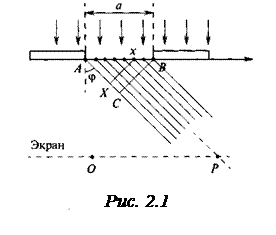
Пусть на бесконечно длинную щель падает плоская световая волна. В соответствии с принципом Гюйгенса-Френеля освещенную щель можно рассматривать как множество точечных когерентных источников волн. Поместим за щелью экран, расстояние до которого достаточно велико по сравнению с шириной щели. Это условие означает, что в данную точку Р экрана попадет параллельный пучок лучей, отклонившийся на угол φ (рис. 2.1). Оптическая разность хода АС=Δ крайних лучей из этого пучка определяется из треугольника ABC ( ):
):
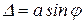 , (2.1)
, (2.1)
где а =АВ – ширина щели. Разобьем щель на зоны Френеля, параллельные щели: оптическая разность хода лучей, идущих от соседних зон, равна половине длины волны, то есть колебания в них происходят в противофазе. Если при наблюдении из точки Р в щели помещается четное число зон Френеля:
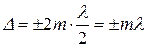 , (2.2)
, (2.2)
то их вклады взаимно погасятся и в точке Р будет наблюдаться минимум интенсивности света. Таким образом, из (2.1) и (2.2) получим условие дифракционных минимумов при дифракции на щели:
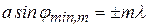 ; (m =1, 2, 3,…) (2.3)
; (m =1, 2, 3,…) (2.3)
где угол 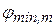 – направление на минимум с номером m.
– направление на минимум с номером m.
Если разность хода крайних лучей равна нечетному числу полуволн:
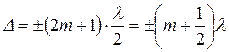 , (2.4)
, (2.4)
то при наблюдении из точки Р в щели помещается нечетное число зон Френеля. Каждая зона гасит соседнюю, а оставшаяся последняя посылает свет в направлении 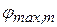 и образует максимум. Поэтому условие максимумов имеет вид:
и образует максимум. Поэтому условие максимумов имеет вид:
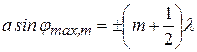 ; (m =1, 2, 3,…) (2.5)
; (m =1, 2, 3,…) (2.5)
Соображения, приводящие к выражениям (2.3) и (2.5), имеют, вообще говоря, приближенный характер, поскольку мы применили метод зон Френеля для бесконечно удаленных точек наблюдения, рассматривая дифракцию в параллельных лучах, однако условие минимумов (2.3) оказывается точным.
Что же касается «центральной» точки О экрана, расположенной против центра щели, то в нее попадает пучок неотклонённых лучей, ортогональных щели. Все они имеют одинаковую фазу, т. е. должны усиливать друг друга. Поэтому в условии минимумов (2.3) исключено значение m =0, соответствующее точке О.
Значение m =0 исключено и из условия максимумов (2.5), поскольку этот максимум должен был бы расположиться между центральным максимумом и первым минимумом, что невозможно.
Точные расчёты показывают, что при наложении всех вторичных волн, идущих под углом j от каждой точки щели, с учётом их амплитуд и фаз, амплитуда результирующего колебания имеет вид:
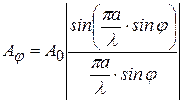 . (2.6)
. (2.6)
Для точки О, лежащей против центра щели, угол φ=0 и Аφ=А0. Этот результат следует, как мы видели, и из физических рассуждений. Следующий за ним первый максимум можно найти при решении уравнения 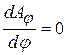 , что даёт:
, что даёт:
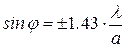 . (2.7)
. (2.7)
 Из приближенного выражения (2.5) при m =1 следует коэффициент 1.5 вместо правильного 1.43, что приводит к погрешности всего лишь в 5%. Для других максимумов согласие с приближенной формулой становится еще лучше. При углах φ, удовлетворяющих условию
Из приближенного выражения (2.5) при m =1 следует коэффициент 1.5 вместо правильного 1.43, что приводит к погрешности всего лишь в 5%. Для других максимумов согласие с приближенной формулой становится еще лучше. При углах φ, удовлетворяющих условию  (m =1, 2, 3,...), амплитуда
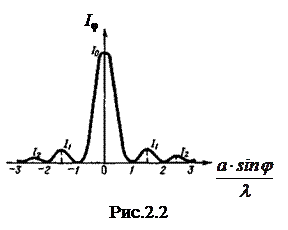
(m =1, 2, 3,...), амплитуда 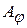 , как видно из (2.6), равна нулю. Это условие определяет положение минимумов, как и было получено выше в (2.3). На рис.2.2 представлена зависимость интенсивности света от угла дифракции.
, как видно из (2.6), равна нулю. Это условие определяет положение минимумов, как и было получено выше в (2.3). На рис.2.2 представлена зависимость интенсивности света от угла дифракции.
Date: 2015-08-06; view: 387; Нарушение авторских прав