да лучей, идущих от двух соседних щелей, будут для данного направления θ одинаковы в пределах всей дифракционной решетки:
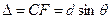 . (7.5)
Очевидно, что в тех направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, т.е. прежние (главные) минимумы интенсивности будут наблюдаться в направлениях, определяемых условием (7.2). Кроме того, вследствие взаимной интерференции световых лучей, посылаемых двумя щелями, в некоторых направлениях они будут гасить друг друга, т.е. возникнут дополнительные минимумы. Эти дополнительные минимумы будут наблюдаться в тех направлениях, которым соответствует разность хода лучей λ/2, 3λ/2, …, посылаемых, например, от крайних левых точек М и С обеих щелей. Таким образом, с учетом (7.5), условие дополнительных минимумов имеет вид: . (7.5)
Очевидно, что в тех направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, т.е. прежние (главные) минимумы интенсивности будут наблюдаться в направлениях, определяемых условием (7.2). Кроме того, вследствие взаимной интерференции световых лучей, посылаемых двумя щелями, в некоторых направлениях они будут гасить друг друга, т.е. возникнут дополнительные минимумы. Эти дополнительные минимумы будут наблюдаться в тех направлениях, которым соответствует разность хода лучей λ/2, 3λ/2, …, посылаемых, например, от крайних левых точек М и С обеих щелей. Таким образом, с учетом (7.5), условие дополнительных минимумов имеет вид:
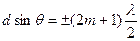 (m = 0, 1, 2, …). (7.6)
Наоборот, действие одной щели будет усиливать действие другой, если (m = 0, 1, 2, …). (7.6)
Наоборот, действие одной щели будет усиливать действие другой, если
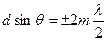 (m = 0, 1, 2, …), (7.7)
т.е. выражение (7.7) задает условие главных максимумов.
Если дифракционная решетка состоит из N щелей, то условием главных минимумов является условие (7.2), условием главных максимумов – условие (7.7), а условием дополнительных минимумов (m = 0, 1, 2, …), (7.7)
т.е. выражение (7.7) задает условие главных максимумов.
Если дифракционная решетка состоит из N щелей, то условием главных минимумов является условие (7.2), условием главных максимумов – условие (7.7), а условием дополнительных минимумов
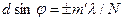 ( (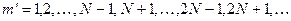 ), (7.8)
где ), (7.8)
где 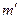 может принимать все целочисленные значения, кроме 0, N, 2N, …, т.е. кроме тех, при которых условие (7.8) переходит в (7.7). Следовательно, в случае N щелей между двумя главными максимумами располагается N – 1 дополнительных минимумов, разделенных вторичными максимумами, создающими весьма слабый фон.
Чем больше щелей N, тем большее количество световой энергии пройдет через решетку, тем больше минимумов образуется меж может принимать все целочисленные значения, кроме 0, N, 2N, …, т.е. кроме тех, при которых условие (7.8) переходит в (7.7). Следовательно, в случае N щелей между двумя главными максимумами располагается N – 1 дополнительных минимумов, разделенных вторичными максимумами, создающими весьма слабый фон.
Чем больше щелей N, тем большее количество световой энергии пройдет через решетку, тем больше минимумов образуется меж | |



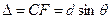 . (7.5)
Очевидно, что в тех направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, т.е. прежние (главные) минимумы интенсивности будут наблюдаться в направлениях, определяемых условием (7.2). Кроме того, вследствие взаимной интерференции световых лучей, посылаемых двумя щелями, в некоторых направлениях они будут гасить друг друга, т.е. возникнут дополнительные минимумы. Эти дополнительные минимумы будут наблюдаться в тех направлениях, которым соответствует разность хода лучей λ/2, 3λ/2, …, посылаемых, например, от крайних левых точек М и С обеих щелей. Таким образом, с учетом (7.5), условие дополнительных минимумов имеет вид:
. (7.5)
Очевидно, что в тех направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, т.е. прежние (главные) минимумы интенсивности будут наблюдаться в направлениях, определяемых условием (7.2). Кроме того, вследствие взаимной интерференции световых лучей, посылаемых двумя щелями, в некоторых направлениях они будут гасить друг друга, т.е. возникнут дополнительные минимумы. Эти дополнительные минимумы будут наблюдаться в тех направлениях, которым соответствует разность хода лучей λ/2, 3λ/2, …, посылаемых, например, от крайних левых точек М и С обеих щелей. Таким образом, с учетом (7.5), условие дополнительных минимумов имеет вид:
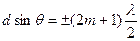 (m = 0, 1, 2, …). (7.6)
Наоборот, действие одной щели будет усиливать действие другой, если
(m = 0, 1, 2, …). (7.6)
Наоборот, действие одной щели будет усиливать действие другой, если
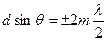 (m = 0, 1, 2, …), (7.7)
т.е. выражение (7.7) задает условие главных максимумов.
Если дифракционная решетка состоит из N щелей, то условием главных минимумов является условие (7.2), условием главных максимумов – условие (7.7), а условием дополнительных минимумов
(m = 0, 1, 2, …), (7.7)
т.е. выражение (7.7) задает условие главных максимумов.
Если дифракционная решетка состоит из N щелей, то условием главных минимумов является условие (7.2), условием главных максимумов – условие (7.7), а условием дополнительных минимумов
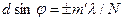 (
(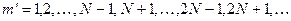 ), (7.8)
где
), (7.8)
где 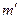 может принимать все целочисленные значения, кроме 0, N, 2N, …, т.е. кроме тех, при которых условие (7.8) переходит в (7.7). Следовательно, в случае N щелей между двумя главными максимумами располагается N – 1 дополнительных минимумов, разделенных вторичными максимумами, создающими весьма слабый фон.
Чем больше щелей N, тем большее количество световой энергии пройдет через решетку, тем больше минимумов образуется меж
может принимать все целочисленные значения, кроме 0, N, 2N, …, т.е. кроме тех, при которых условие (7.8) переходит в (7.7). Следовательно, в случае N щелей между двумя главными максимумами располагается N – 1 дополнительных минимумов, разделенных вторичными максимумами, создающими весьма слабый фон.
Чем больше щелей N, тем большее количество световой энергии пройдет через решетку, тем больше минимумов образуется меж
 и
и  .
.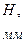
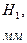
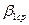
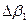
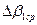
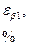
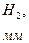
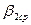
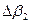
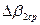
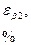
 7.2. Дифракция Фраунгофера на дифракционной решетке.
Одномерной дифракционной решеткой называется система параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками. Как было показано выше, при дифракции Фраунгофера на одной щели распределение интенсивности на экране определяется направлением дифрагированных лучей. Это означает, что перемещение щели параллельно самой себе влево или вправо не изменит дифракционной картины. Следовательно, если перейти от одной щели ко многим (к дифракционной решетке), то дифракционные картины, создаваемые каждой щелью в отдельности будут одинаковыми. Дифракционная картина на решетке возникает как результат взаимной интерференции волн, идущих от всех щелей.
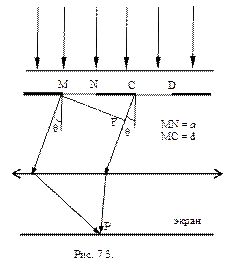
Рассмотрим дифракционную решетку. На рис. 7.3. для наглядности показаны только две соседние щели MN и CD; ширина каждой щели равна a. Расстояние d между серединами (или соответствующими краями) соседних щелей называется постоянной (периодом) дифракционной решетки. Пусть плоская монохроматическая световая волна падает нормально к плоскости решетки. Так как щели находятся друг от друга на одинаковых расстояниях, то разности хо
7.2. Дифракция Фраунгофера на дифракционной решетке.
Одномерной дифракционной решеткой называется система параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками. Как было показано выше, при дифракции Фраунгофера на одной щели распределение интенсивности на экране определяется направлением дифрагированных лучей. Это означает, что перемещение щели параллельно самой себе влево или вправо не изменит дифракционной картины. Следовательно, если перейти от одной щели ко многим (к дифракционной решетке), то дифракционные картины, создаваемые каждой щелью в отдельности будут одинаковыми. Дифракционная картина на решетке возникает как результат взаимной интерференции волн, идущих от всех щелей.
Рассмотрим дифракционную решетку. На рис. 7.3. для наглядности показаны только две соседние щели MN и CD; ширина каждой щели равна a. Расстояние d между серединами (или соответствующими краями) соседних щелей называется постоянной (периодом) дифракционной решетки. Пусть плоская монохроматическая световая волна падает нормально к плоскости решетки. Так как щели находятся друг от друга на одинаковых расстояниях, то разности хо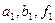 с
с 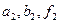 ?
?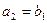 и
и 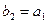 ? Почему они должны выполняться?
? Почему они должны выполняться?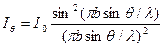 . (7.4)
График функции (7.4) показан на рис. 7.2. Расчеты по данной формуле показывают, что интенсивности в центральном и последующих максимумах относятся как 1:0,047:0,017:0,0083:…, т.е. основная часть световой энергии сосредоточена в центральном максимуме. Из опыта и соответствующих расчетов следует, что сужение щели приводит к тому, что центральный максимум расплывается, а интенсивность уменьшается (это относится и к другим максимумам). Наоборот, чем щель шире (а > λ), тем картина ярче, но дифракционные полосы уже, а число самих полос больше. При
. (7.4)
График функции (7.4) показан на рис. 7.2. Расчеты по данной формуле показывают, что интенсивности в центральном и последующих максимумах относятся как 1:0,047:0,017:0,0083:…, т.е. основная часть световой энергии сосредоточена в центральном максимуме. Из опыта и соответствующих расчетов следует, что сужение щели приводит к тому, что центральный максимум расплывается, а интенсивность уменьшается (это относится и к другим максимумам). Наоборот, чем щель шире (а > λ), тем картина ярче, но дифракционные полосы уже, а число самих полос больше. При 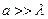 в центре получается резкое изображение источника света, т.е. имеет место прямолинейное распространение света.
в центре получается резкое изображение источника света, т.е. имеет место прямолинейное распространение света.
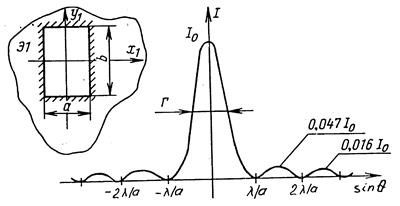 Рис. 7.2.
Рис. 7.2.
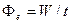 . (3.1)
Единица потока излучения – ватт (Вт).
Энергетическая светимость (излучательность)Re – величина, равная отношению потока излучения Φe, испускаемого поверхностью, к площади S сечения, сквозь которое этот поток проходит:
. (3.1)
Единица потока излучения – ватт (Вт).
Энергетическая светимость (излучательность)Re – величина, равная отношению потока излучения Φe, испускаемого поверхностью, к площади S сечения, сквозь которое этот поток проходит:
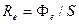 , (3.2)
, (3.2)
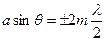 (m = 1, 2, 3, …), (7.2)
и в точке Р наблюдается дифракционный минимум (полная темнота), если же число зон Френеля нечетное, то
(m = 1, 2, 3, …), (7.2)
и в точке Р наблюдается дифракционный минимум (полная темнота), если же число зон Френеля нечетное, то
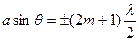 (m = 1, 2, 3, …), (7.3)
и наблюдается дифракционный максимум, соответствующий действию одной нескомпенсированной зоны Френеля. Отметим, что в направлении
(m = 1, 2, 3, …), (7.3)
и наблюдается дифракционный максимум, соответствующий действию одной нескомпенсированной зоны Френеля. Отметим, что в направлении 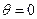 щель действует как одна зона Френеля, и в этом направлении свет распространяется с наибольшей интенсивностью, т.е. в точке Р0 наблюдается центральный дифракционный максимум.
Из условий (7.2) и (7.3) можно найти направления на точки экрана, в которых амплитуда (а следовательно и интенсивность) света равна нулю (
щель действует как одна зона Френеля, и в этом направлении свет распространяется с наибольшей интенсивностью, т.е. в точке Р0 наблюдается центральный дифракционный максимум.
Из условий (7.2) и (7.3) можно найти направления на точки экрана, в которых амплитуда (а следовательно и интенсивность) света равна нулю (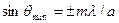 ) или максимальна (
) или максимальна (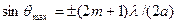 ). Распределение интенсивности на экране, получаемое вследствие дифракции (дифракционный спектр) показано на рис. 7.2. Интенсивность света Iθ в точке, расположение которой характеризуется углом θ и интенсивность I0 в точке Р0, расположенной в центре дифракционной картины (против центра линзы) связаны между собой соотношением
). Распределение интенсивности на экране, получаемое вследствие дифракции (дифракционный спектр) показано на рис. 7.2. Интенсивность света Iθ в точке, расположение которой характеризуется углом θ и интенсивность I0 в точке Р0, расположенной в центре дифракционной картины (против центра линзы) связаны между собой соотношением
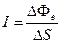 , (3.3)
где Δ S – малая поверхность, перпендикулярная направлению распространения излучения, через которую переносится поток ΔΦе.
Единица измерения интенсивности излучения такая же, как у энергетической светимости –Вт/м2.
, (3.3)
где Δ S – малая поверхность, перпендикулярная направлению распространения излучения, через которую переносится поток ΔΦе.
Единица измерения интенсивности излучения такая же, как у энергетической светимости –Вт/м2.
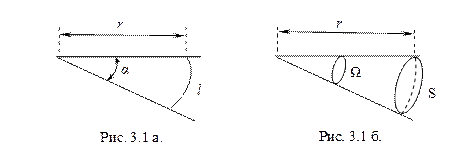 Для определения последующих величин понадобится использовать одно геометрическое понятие – телесный угол, который является мерой раствора некоторой конической поверхности. Как известно, мерой плоского угла является отношение дуги окружности l к радиусу этой окружности r, т.е.
Для определения последующих величин понадобится использовать одно геометрическое понятие – телесный угол, который является мерой раствора некоторой конической поверхности. Как известно, мерой плоского угла является отношение дуги окружности l к радиусу этой окружности r, т.е. 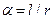 (рис. 3.1 а). Аналогично этому определяется телесный угол Ω (рис. 3.1 б) как отношение поверхности шарового сегмента S к квадрату радиуса сферы:
(рис. 3.1 а). Аналогично этому определяется телесный угол Ω (рис. 3.1 б) как отношение поверхности шарового сегмента S к квадрату радиуса сферы:
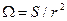 . (3.4)
Единицей измерения телесного угла служит стерадиан (ср) – это телесный угл, вершина которого расположена в центре сферы, и который вырезает на поверхности сферы площадь, равную квадрату радиуса: Ω = 1 ср, если
. (3.4)
Единицей измерения телесного угла служит стерадиан (ср) – это телесный угл, вершина которого расположена в центре сферы, и который вырезает на поверхности сферы площадь, равную квадрату радиуса: Ω = 1 ср, если 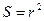 . Нетрудно убедиться, что полный те
. Нетрудно убедиться, что полный те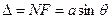 , (7.1)
где F – основание перпендикуляра, опущенного из точки М на луч ND.
Разобьем открытую часть волновой поверхности в плоскости щели MN на зоны Френеля (см. раздел 6.2), имеющие вид полос, параллельных ребру М щели. Ширина каждой зоны выбирается так,
, (7.1)
где F – основание перпендикуляра, опущенного из точки М на луч ND.
Разобьем открытую часть волновой поверхности в плоскости щели MN на зоны Френеля (см. раздел 6.2), имеющие вид полос, параллельных ребру М щели. Ширина каждой зоны выбирается так,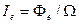 . (3.5)
Единица энергетической силы света – ватт на стерадиан (Вт/ср).
Энергетическая яркость (лучистость)Ве – величина, равная отношению энергетической силы света ΔIe элемента излучающей поверхности к площади ΔS проекции этого элемента на плоскость, перпендикулярную направлению наблюдения:
. (3.5)
Единица энергетической силы света – ватт на стерадиан (Вт/ср).
Энергетическая яркость (лучистость)Ве – величина, равная отношению энергетической силы света ΔIe элемента излучающей поверхности к площади ΔS проекции этого элемента на плоскость, перпендикулярную направлению наблюдения:
 . (3.6)
Единица энергетической яркости – ватт на стерадиан-метр в квадрате (Вт/(ср·м2)).
Энергетическая освещенность (облученность)Ее характеризует величину потока излучения, падающего на единицу освещаемой поверхности. Единица энергетической освещенности совпадает с единицей энергетической светимости (Вт/м2).
2. Световые величины. При оптических измерениях используются различные приемники излучения (например, глаз, фотоэлементы, фотоумножители), которые не обладают одинаковой чувствительностью к энергии различных длин волн, являясь, таким образом, селективными (избирательными). Каждый приемник светового излучения характеризуется своей кривой чувствительности к свету раз
. (3.6)
Единица энергетической яркости – ватт на стерадиан-метр в квадрате (Вт/(ср·м2)).
Энергетическая освещенность (облученность)Ее характеризует величину потока излучения, падающего на единицу освещаемой поверхности. Единица энергетической освещенности совпадает с единицей энергетической светимости (Вт/м2).
2. Световые величины. При оптических измерениях используются различные приемники излучения (например, глаз, фотоэлементы, фотоумножители), которые не обладают одинаковой чувствительностью к энергии различных длин волн, являясь, таким образом, селективными (избирательными). Каждый приемник светового излучения характеризуется своей кривой чувствительности к свету раз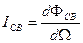 , (3.7)
где dΦсв – световой поток, излучаемый источником в пределах телесного угла dΩ. Если Iсв не зависит от направления, источник света называется изотропным. Для изотропного источника
, (3.7)
где dΦсв – световой поток, излучаемый источником в пределах телесного угла dΩ. Если Iсв не зависит от направления, источник света называется изотропным. Для изотропного источника
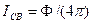 . (3.8)
Поток энергии . Φе, измеряемый в ваттах, и световой поток Φ св, измеряемый в люменах, связаны соотношением:
. (3.8)
Поток энергии . Φе, измеряемый в ваттах, и световой поток Φ св, измеряемый в люменах, связаны соотношением:
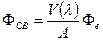 , лм, (3.9)
где
, лм, (3.9)
где 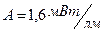 - константа,
- константа, 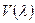 - функция видности, определя
- функция видности, определя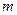
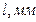
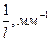

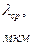
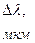
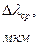
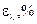
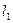 от риски модуля 8 до точки фокусировки волны (первоначального положения риски микропроектора) будет постоянным. Зная
от риски модуля 8 до точки фокусировки волны (первоначального положения риски микропроектора) будет постоянным. Зная 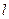 , найдите с помощью (6.25) соответствующие значения
, найдите с помощью (6.25) соответствующие значения 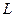 и, учитывая, что
и, учитывая, что 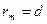 , определите из (6.23) длину волны излучения:
, определите из (6.23) длину волны излучения: 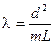 .
.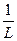 .
.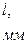
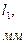
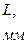
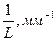
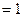 достигается при
достигается при 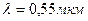 . В комплексе используется лазерное излучение с длиной волны
. В комплексе используется лазерное излучение с длиной волны 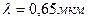 . В этом случае
. В этом случае 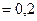 .
СветимостьRсв определяется соотношением
.
СветимостьRсв определяется соотношением
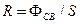 . (3.10)
Единица светимости – люмен на метр в квадрате (лм/м2).
Яркость Вφ светящейся поверхности площадью S в некотором направлении, образующем угол φ с нормалью к поверхности, есть величина, равная отношению силы света в данном направлении к площади проекции светящейся поверхности на плоскость, перпендикулярную данному направлению:
. (3.10)
Единица светимости – люмен на метр в квадрате (лм/м2).
Яркость Вφ светящейся поверхности площадью S в некотором направлении, образующем угол φ с нормалью к поверхности, есть величина, равная отношению силы света в данном направлении к площади проекции светящейся поверхности на плоскость, перпендикулярную данному направлению:
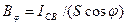 . (3.11)
Источники, яркость которых одинакова по всем направлениям, называются ламбертовскими (подчиняющимися закону Ламберта) или косинусными (поток, посылаемый элементом поверхности такого источника, пропорционален
. (3.11)
Источники, яркость которых одинакова по всем направлениям, называются ламбертовскими (подчиняющимися закону Ламберта) или косинусными (поток, посылаемый элементом поверхности такого источника, пропорционален 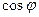 ). Строго следует закону Ламберта только абсолютно черное тело.
Единица яркости – кандела на метр в квадрате (кд/м2).
Освещенность Е – величина, равная отношению светового потока, падающего на поверхность, к площади этой поверхности:
). Строго следует закону Ламберта только абсолютно черное тело.
Единица яркости – кандела на метр в квадрате (кд/м2).
Освещенность Е – величина, равная отношению светового потока, падающего на поверхность, к площади этой поверхности:
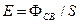 . (3.12)
Единица освещенности – люкс (лк): 1 лк – освещенность поверхности, на 1 м2 которой падает световой поток в 1 лм (1 лм = 1 лк/м2).
Порядок выполнения работы
. (3.12)
Единица освещенности – люкс (лк): 1 лк – освещенность поверхности, на 1 м2 которой падает световой поток в 1 лм (1 лм = 1 лк/м2).
Порядок выполнения работы
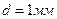 ) и придвиньте этот модуль вплотную к объективу.
4. С помощью юстировочных винтов модуля 8 установите отверстие на оси пучка света и получите на экране установки дифракционную картину. Расстояние
) и придвиньте этот модуль вплотную к объективу.
4. С помощью юстировочных винтов модуля 8 установите отверстие на оси пучка света и получите на экране установки дифракционную картину. Расстояние 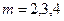 и т. д. зоны Френеля. В начале движения вы будете наблюдать светлое пятно в центре картины. Считайте его первой зоной. Затем, по мере приближения к модулю 8, в центре светлого пятна возникнет темное пятно, и вы будете иметь уже две зоны Френеля… И так вплоть до соприкосновения микропроектора с двухкоординатным держателем.
6. Постройте график зависимости
и т. д. зоны Френеля. В начале движения вы будете наблюдать светлое пятно в центре картины. Считайте его первой зоной. Затем, по мере приближения к модулю 8, в центре светлого пятна возникнет темное пятно, и вы будете иметь уже две зоны Френеля… И так вплоть до соприкосновения микропроектора с двухкоординатным держателем.
6. Постройте график зависимости  .
7. Учитывая, что в данном случае
.
7. Учитывая, что в данном случае 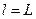 ,
, 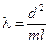 .
8. Результаты занесите в таблицу:
.
8. Результаты занесите в таблицу:
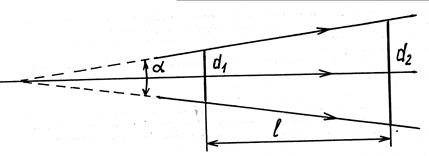 Рис. 3.2.
Измерив диаметр расходящегося пучка лазера в двух его сечениях, разнесенных на расстояние
Рис. 3.2.
Измерив диаметр расходящегося пучка лазера в двух его сечениях, разнесенных на расстояние 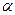 и телесный угол
и телесный угол 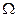 , в котором распространяется излучение (рис. 3.2):
, в котором распространяется излучение (рис. 3.2):
 , (3.13)
, (3.13)
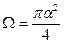 . (3.14)
Сила света в канделлах определяется по формуле:
. (3.14)
Сила света в канделлах определяется по формуле:
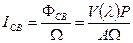 , (3.15)
где
, (3.15)
где 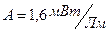 - константа, мощность излучения
- константа, мощность излучения  устанавливается минимальной - равной
устанавливается минимальной - равной 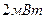 (ручка регулировки тока лазера повернута до крайнего положения против часовой стрелки),
(ручка регулировки тока лазера повернута до крайнего положения против часовой стрелки), 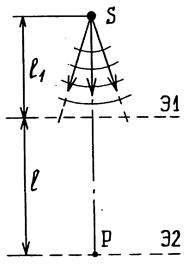
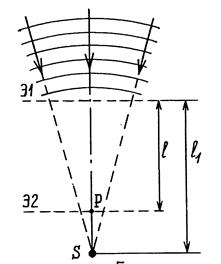 Рис. 6.8. Рис. 6.9.
Если на экран Э1 падает расходящаяся волна от точечного источника S (рис. 6.8) или волна, сходящаяся в точке S (рис. 6.9), то вычисление фазовых сдвигов и количества открытых зон Френеля приводят к тем же формулам (6.21)-(6.22), что и для плоской волны, в которых, однако,
Рис. 6.8. Рис. 6.9.
Если на экран Э1 падает расходящаяся волна от точечного источника S (рис. 6.8) или волна, сходящаяся в точке S (рис. 6.9), то вычисление фазовых сдвигов и количества открытых зон Френеля приводят к тем же формулам (6.21)-(6.22), что и для плоской волны, в которых, однако, 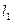 от фокуса волны до экрана Э1 и расстояние
от фокуса волны до экрана Э1 и расстояние 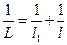 . (6.24)
Для сходящейся волны
. (6.24)
Для сходящейся волны
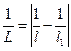 . (6.25)
Плоской волне, очевидно, соответствует
. (6.25)
Плоской волне, очевидно, соответствует 
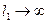 ,
, 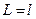 .
Эксперимент
1. Оснащение установки то же, что и в предыдущем задании, только кассета модуля 8 должна быть пуста.
2. С помощью модулей 5 и 6 создайте параллельный пучок
.
Эксперимент
1. Оснащение установки то же, что и в предыдущем задании, только кассета модуля 8 должна быть пуста.
2. С помощью модулей 5 и 6 создайте параллельный пучок