
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Определить вид линии, изобразить линию на чертеже и написать формулы преобразования
|
|
Задача 30
Исследовать кривую второго порядка g на плоскости R2 и построить ее. В ответе написать каноническое уравнение кривой и формулы преобразования координат.
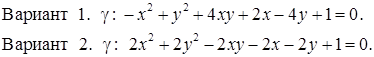
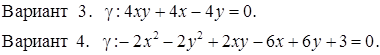
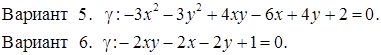
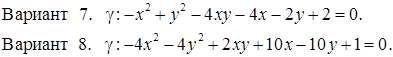
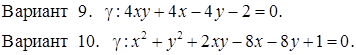
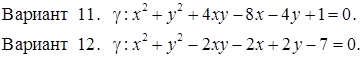
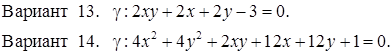
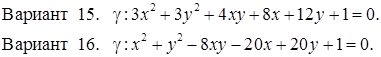
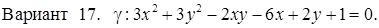
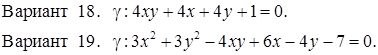
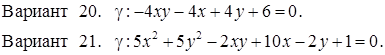
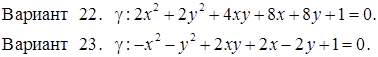
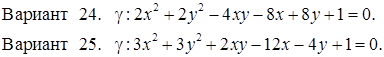
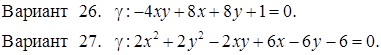
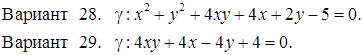
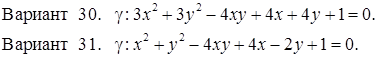
РЕШЕНИЯ ТИПОВЫХ Примеров
Пример 1. Поворотом прямоугольной декартовой системы координат привести к каноническому виду уравнение линии второго порядка
5 x2 + 8 xy +5 y2 - 9= 0. (1)
Определить вид линии, изобразить линию на чертеже и написать формулы преобразования.
Решение.
1) Запишем характеристическое уравнение для данной линии и найдем его корни. Имеем
а 11 =5, а 12=4, а 22 = 5, а 13= 0, а 23 =0, а 33 = -9;
l2 - 10l + 9 = 0, 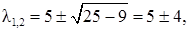 l1 = 1, l2 = 9.
l1 = 1, l2 = 9.
2) Найдем угол поворота системы координат XOY такой, чтобы a` 12 = 0:
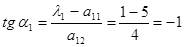 ,
, 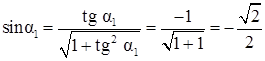 ,
, 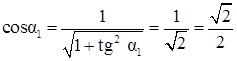 ,
, 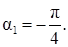
3) Найдем коэффициенты 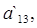
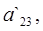
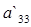 :
:
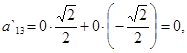
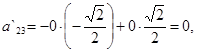
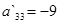 .
.
Уравнение линии g в системе координат X ` O ` Y `, O `= O имеет вид 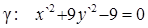
или
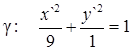 . (2)
. (2)
Это уравнение задает эллипс.
4) Построим систему координат X`O`Y`, полученную поворотом на угол 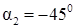 (или на
(или на 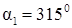 ) системы координат XOY и в X`O`Y` выполним построение эллипса (рис. 1).
) системы координат XOY и в X`O`Y` выполним построение эллипса (рис. 1).
         Y
Y'
g
X
45º
X'
Рис. 1 Y
Y'
g
X
45º
X'
Рис. 1
|
 5) Формулы преобразования системы координат XOY имеют вид
5) Формулы преобразования системы координат XOY имеют вид
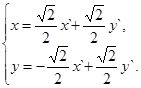 (3)
(3)
Замечание 1. Уравнение линии в виде (2) из (1) можно получить непосред -ственно, подставляя в (1) формулы преобразования (3). В самом деле,
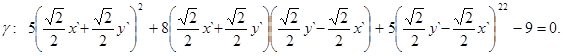
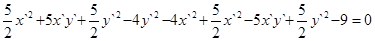 ,
, 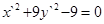 ,
,
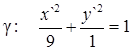 . Получаем то же уравнение (2)
. Получаем то же уравнение (2)
Ответ: Эллипс 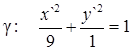 ; см. рис.1;
; см. рис.1; 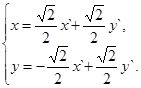
Пример 2. С помощью переноса начала прямоугольной декартовой системы координат привести к каноническому виду уравнение линии второго порядка
g: 2 x 2- 8 x + 4 y + 9 = 0. (4)
Определить вид линии, изобразить линию на чертеже и написать формулы преобразования системы координат.
Решение.
1) Сгруппируем члены в левой части данного уравнения относительно x и y следующим образом
2(x 2 - 2 x 2 + 4) - 8 + 4 y + 9 = 2(x - 2)2+4(y + 1/4) = 0.
2) Введем обозначения
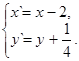 Þ
Þ 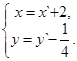
Совершим параллельный перенос системы координат XOY на вектор 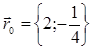 .
.
3) Уравнение данной линии в системе координат X`O`Y` имеет вид 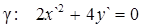 или
или
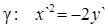 . (5)
. (5)
4) Построим систему координат X`O`Y`, полученную переносом на вектор 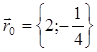 системы координат XOY и в X`O`Y` выполним построение параболы (рис.2)
системы координат XOY и в X`O`Y` выполним построение параболы (рис.2) 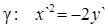 .
.
          Y Y'
0
X
0' X'
Рис. 2 g Y Y'
0
X
0' X'
Рис. 2 g
|
5) Формулы преобразования системы координат XOY имеют вид
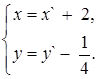 (6)
(6)
Как и в примере 1 можно показать, что (5) получается из (4) формулами преобразований (6).
Ответ: Парабола 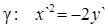 ; см. рис.2;
; см. рис.2; 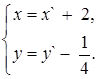
Пример 3. Поворотом прямоугольной декартовой системы координат и параллельным переносом привести к каноническому виду уравнение линии второго порядка
g: 29 x2 + 144 xy + 71 y2 - 40 x + 30 y – 50 = 0. (7)
Определить вид линии, изобразить линию на чертеже и написать формулы преобразования системы координат.
Решение. а 11= 29, а 12= 72, а 22= 71, а 13= -20, а 23= 15, а 33 = -50.
1) Найдем корни характеристического уравнения
l2 - 100l - 3125 = 0, l1 = -25, l2 = 125.
2) Найдем угол поворота системы координат XOY такой, чтобы а` 12= 0:
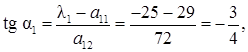
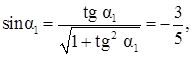 ,
, 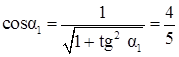 Þ
Þ 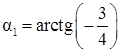 ,
, 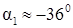 .
.
3) Найдем коэффициенты 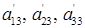 :
:
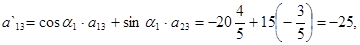
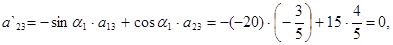
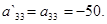 .
.
После поворота системы координат XOY на угол 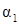 уравнение линии g имеет вид
уравнение линии g имеет вид 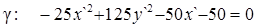 или, после деления обеих частей на –25, следующий вид.
или, после деления обеих частей на –25, следующий вид.
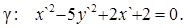 (8)
(8)
4) Совершим параллельный перенос системы координат X`O`Y`, O` = O. Для этого сделаем следующие преобразования
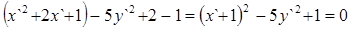 .
.
Возьмем новую систему координат X``O``Y`` так, чтобы формулы преобразования имели вид
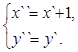 или
или 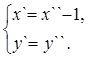 (9)
(9)
т.е. она получена из системы координат X`O`Y` параллельным переносом на вектор 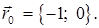
В системе координат X``O``Y`` уравнение линии g записывается так 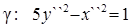 или
или
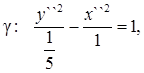 (10)
(10)
т.е. линия представляет из себя гиперболу.
5) Построим систему координат X`O`Y`, O` = O, полученную из системы координат XOY поворотом на угол 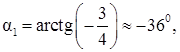 а затем X``O``Y``, полученную из X`O`Y` параллельным переносом на вектор
а затем X``O``Y``, полученную из X`O`Y` параллельным переносом на вектор 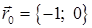 и в X``O``Y`` выполним построение гиперболы (рис.3)
и в X``O``Y`` выполним построение гиперболы (рис.3) 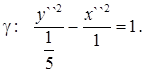
|

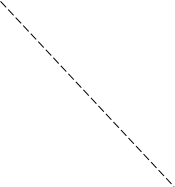
 6) Напишем формулы преобразования системы координат.
6) Напишем формулы преобразования системы координат.
а) Поворот на угол 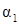 в XOY:
в XOY:



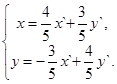 (11)
(11)
б) Параллельный перенос в X`O`Y`:
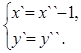 (12)
(12)
в) Тогда общие формулы преобразования системы координат, при котором происходит переход от системы координат XOY к X``O``Y`` примут вид:
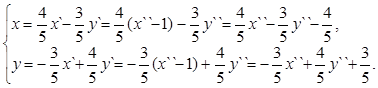 (13)
(13)
или
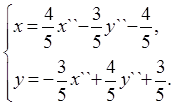 (14)
(14)
Замечание 2. Уравнение линии в виде (10) из (7) можно получить непосредственно, подставляя в (7) формулы преобразования (14). Читателю предоставляем самостоятельно убедиться в этом (см. рассуждения в замечании 1).
Ответ: Гипербола 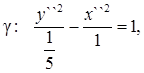 ; см. рис.3;
; см. рис.3;
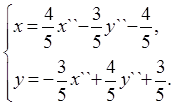
| <== предыдущая | | | следующая ==> |
| тренинг по решению задач | | | Введение. Глава 1. Понятие недействительной сделки |
Date: 2015-07-27; view: 1112; Нарушение авторских прав