Метод LU-факторизации

В методе LU-факторизации (эту схему называют компактной схемой Гаусса) при решении системы 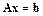выполняется следующая последовательность действий.

Матрица 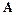представляется в виде произведения

,

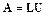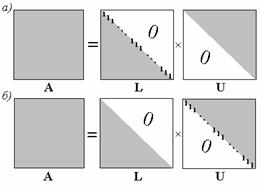
Рис. 2.3. Структура матриц L и U в разложениях Дулиттла (а) и Краута (б)

где L - нижняя треугольная матрица, U - верхняя треугольная матрица. Такое разложение единственно при условии предварительного выбора диагональных элементов одной из матриц. В этом случае число элементов в матрице A совпадает с суммарным числом неизвестных элементов матриц L и U. Если диагональ L принимается единичной, то такое разложение называют разложением Дулиттла (рис. 2.3,а), если единична диагональ U – разложением Краута (рис. 2.3,б). В дальнейшем при построении метода LU- факторизации будем привлекать разложение Краута.

Система 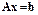заменяется системой

,

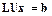легко решаемой за два шага:

Шаг 1. 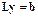. Принимая во внимание треугольный вид матрицы L, нетрудно получить, что в алгоритме Краута

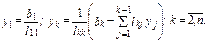
Шаг 2. 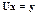. Решение этой системы в алгоритме Краута:

.

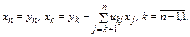Суммарные затраты реализации обоих шагов при n>> 1 составляют 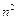длинных операций.

Получим соотношения для расчета элементов матриц L и U в алгоритме Краута. Для этого перемножим матрицы L и U и приравняем результат к A. По правилу перемножения матриц

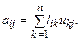
Учтем, что

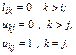
Рассмотрим элемент 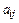(рис. 2.4), расположенный на центральной диагонали либо в нижней треугольной части матрицы A. Для такого элемента i ≥ j. Из рисунка следует, что

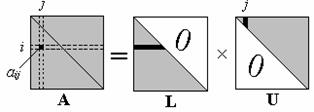
Рис. 2.4. Иллюстрация вычисления элемента матрицы, расположенного

ниже главной диагонали

,

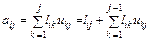так как i ≥ j и 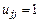. Отсюда

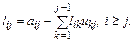
Рассмотрим элемент 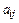(рис. 2.5), находящийся выше главной

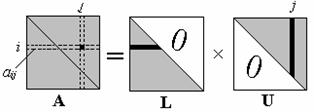
Рис. 2.5. Иллюстрация вычисления элемента матрицы, расположенного

выше главной диагонали

диагонали матрицы A (для него j>i). В этом случае

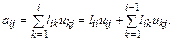
Следовательно,

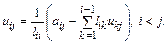
Получили в итоге соотношения, которые позволяют вычислять элементы матриц L и U. Последовательность вычислений: сначала вычисляется столбец матрицы L, далее строка матрицы U, затем опять столбец матрицы L, далее строка матрицы U и т. д. (см. рис. 2.6, который иллюстрирует последовательность вычислений и схему хранения матриц L и U).

Вычисление столбца матрицы L и строки матрицы U назовем шагом LU-разложения. Приведем в качестве примера схему хранения элементов матриц A, L, U после второго шага LU-разложения (рис. 2.7).

Число длинных арифметических операций на этапе LU-разложения при n>> 1 составляет величину 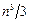, на шаге решения ли-

нейных систем с треугольными матрицами – 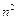. Суммарное число длинных операций приближенно равно 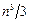(как и в методе Гаусса),

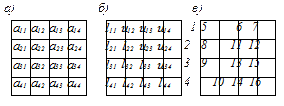
Рис. 2.6. Исходная матрица A (а), схема хранения L и U матриц (б), последовательность вычисления элементов в принятой схеме хранения (в)

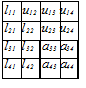
Рис. 2.7 Схема хранения элементов 4´4 матриц A, L, U после второго шага LU-факторизации

т. е. основные затраты приходятся на LU-факторизацию матрицы A. Эта особенность делает особо привлекательным метод LU-факторизации при решении СЛАУ с одной и той же матрицей A, но разными правыми частями:

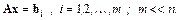
В этом случае факторизация матрицы выполняется однократно, требуя 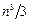длинных операций, а решение каждой системы с соответствующей правой частью реализуется за 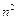таких операций.