Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Уравнение радиального равновесия в турбинной ступени (вывод)
|
|
Поскольку давление р1 вдоль оси а постоянно, то уравнение равновесия всех сил в проекциях на направление радиуса r имеет вид: р1×r×dj×da–(р1+dр1)(r+dr)×dj×da+2 (р1+0,5dp1)×dr×da×sin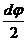 
+ 
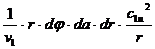=0
Заменив sin(dj/2)»dj/2, после преобразований (членами третьего порядка малости пренебрегаем) получим для сечения «1-1» ступени упрощенный вид уравнения радиального равновесия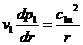 
.
Аналогично получают уравнения и для других сечений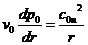 
; 
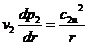. (Применительно к схеме течения, показанной на рис. 9.1, б, где присутствуют составляющие скорости по радиусу (с1r) и вдоль оси а (с1а), уравнение радиального равновесия записывается следующим образом:
.
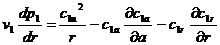В правой части первый член характеризует влияние центробежных сил, а остальные члены – влияние радиального ускорения. Из полученных уравнений радиального равновесия следует, что градиент статического давления вдоль радиуса в сечении за сопловой решеткой ступени пропорционален квадрату окружной составляющей скорости и обратно пропорционален радиусу. Таким образом, если перед ступенью (за ней) окружная составляющая скорости с0u (c2u) равна нулю, т.е. угол a0 (a2) равен 900, то по высоте лопаток перед ступенью (за ней) статическое давление не изменяется.
13.2 Основные законы закруток турбинных решеток (перечень) На основе уравнений радиального равновесия формируются различные законы закручивания лопаток решеток турбинных ступеней.
1. Постоянство углов a1(r)=const. Для этого закона закрутки при условии постоянства коэффициента скорости по радиусу сопловой решетки j(r)=const получено выражение, связывающее изменение скорости с1t и степени реактивности r по радиусу r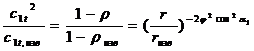 
2. Постоянство циркуляции скорости закрученного потока (сur=const) за сопловой решеткой. Данный закон получают при использовании уравнения энергии, записанного для зазора между решетками ступени в предположении, что энтальпия полного торможения не изменяется по высоте (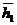
= h1+0,5c12=const), а также при условии с1а=const. Изменение скорости с1 по радиусу выражается соотношением c1ur=c1u,корrкор. Очевидным является уравнение 
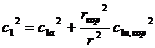, из которого следует, что скорость с1 уменьшается по высоте решетки. Следовательно, давление в зазоре увеличивается от ее корневых сечений к периферийным сечениям. Тогда изменение степени реактивности можно представить уравнением
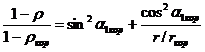. 3 Закон постоянства удельного расхода
4. Закон постоянного профиля сопловых и рабочих лопаток по высоте ступени.
В такой ступени изменение углов a1 и b2 определяется конкретными характеристиками облопачивания, например, зависимостью эффективных углов выхода a1Э и b2Э от относительного шага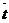 
, которые имеются в атласах профилей.
13.3 Законы постоянства удельного расхода, предполагает неизменность массового расхода на единицу торцевой площади сопловой и рабочей решеток по их высоте: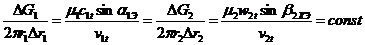 
.
14.1 Предельная мощность однопоточной конденсационной турбины (вывод) Ni=mGкH0тhoiт
Предельная мощность паровой турбины определяется расходом водяного пара через последнюю ступень (G 2), который ограничивается значением абсолютной скорости с2 за ее рабочей решеткой из условия Мс2 <1, удельным объемом влажного пара v2, зависящим от давления рк в конденсаторе, а также площадью рабочей решетки последней ступени F2=pd2l2sina2
Расход пара в конденсатор однопоточной турбины определяется из уравнения неразрывности следующим образом:
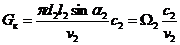, направление абсолютной скорости с2 выбирается с приближением к углу a2 =900 (sina2 =1)
где W2 =pd2l2 – аксиальная (осевая) площадь выхода из рабочих лопаток последней ступени; с2, v2 – осредненные по высоте выходного сечения рабочей решетки значения абсолютной скорости и удельного объема. Максимальные значения напряжения растяжения s р, мах от действия центробежных сил Rцс при вращении ротора с угловой частотой w=2pn имеют место в корневом сечении рабочей лопатки. При постоянном значении площади f л сечений профиля по высоте лопатки
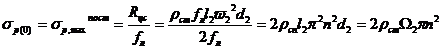, где r ст – плотность материала лопаток,
Поскольку лопатки последних ступеней выполняют с переменным сечением профиля по высоте l2 (площадь сечения уменьшается от корня к периферии рабочей лопатки), что приводит к снижению напряжения sр в корневом сечении, то вследует ввести коэффициент разгрузки k разгр, определяемый отношением площадей сечений у вершины и корня лопатки f пер/ f кор, а также законом изменения площадей по высоте, из выражения: 1/ k разгр»0,35+0,65× f пер/ f кор тогда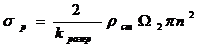 
. Выражаем 
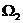и подстановка его в выражение Ni,. 
.
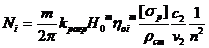Date: 2015-07-27; view: 1533; Нарушение авторских прав