
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основні положення
|
|
В растр необхідно розкладати не тільки лінійні, але і інші, більш складні функції. Один з найбільш ефективних і простих для розуміння алгоритмів генерування кола належить американському вченому Брезенхему.
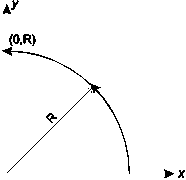
Для початку відзначимо, що необхідно згенерувати тільки 1/8 частину кола. Решта його частин можуть бути отримані послідовними відображеннями, як це показано на рис. 3.1.
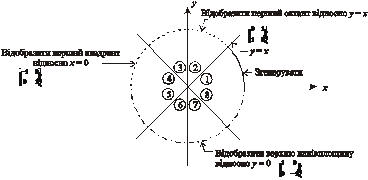
Рис. 3.1. Генерування повного кола з дуги в першому октанті
Зобразимо генерування повного кола з дуги в першому октанті графічно.
Якщо згенерувати перший октант (від 0 до 45° проти годинникової стрілки), то другий октант можна отримати дзеркальним відображенням відносно прямої 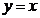 , що дає в цілому перший квадрант.
, що дає в цілому перший квадрант.
Перший квадрант відображається відносно прямої 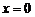 для отримання відповідної частини кола в другому квадранті. Верхнє напівколо відображається відносно прямої y = x
для отримання відповідної частини кола в другому квадранті. Верхнє напівколо відображається відносно прямої y = x 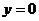 для закінчення побудови. На рисунку 3.1 зображені двовимірні матриці відповідних перетворень.
для закінчення побудови. На рисунку 3.1 зображені двовимірні матриці відповідних перетворень.
Для виводу алгоритму розглянемо першу чверть кола з центром в початку координат. Відзначимо, що якщо робота алгоритму починається в точці 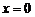
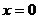 ,
, 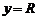
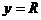 , то при генеруванні кола за годинниковою стрілкою в першому квадранті y є монотонно спадаючою функцією аргументу x (рис. 3.2).
, то при генеруванні кола за годинниковою стрілкою в першому квадранті y є монотонно спадаючою функцією аргументу x (рис. 3.2).
| 
|
| Рис.3.2. Коло в першому квадранті | Рис. 3.3. Вибір пікселів в першому квадранті |
Аналогічно, якщо початковою точкою є  ,
,  , то при генеруванні кола проти годинникової стрілки x буде монотонно спадаючою функцією аргументу y. Вибираємо генерування за годинниковою стрілкою з початком в точці
, то при генеруванні кола проти годинникової стрілки x буде монотонно спадаючою функцією аргументу y. Вибираємо генерування за годинниковою стрілкою з початком в точці 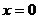 ,
, 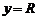 . Передбачається, що центр кола і початкова точка знаходяться точно в точках растру. Для будь-якої заданої точки на колі при генеруванні за годинниковою стрілкою існує тільки три можливості вибрати наступний піксель, який найкращим чином наближається до кола: горизонтальний направо, по діагоналі вниз і вправо, вертикальний вниз.
. Передбачається, що центр кола і початкова точка знаходяться точно в точках растру. Для будь-якої заданої точки на колі при генеруванні за годинниковою стрілкою існує тільки три можливості вибрати наступний піксель, який найкращим чином наближається до кола: горизонтальний направо, по діагоналі вниз і вправо, вертикальний вниз.
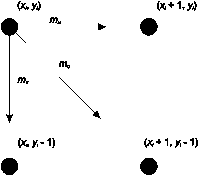
На рис. 3.3 ці напрями позначаються відповідно 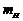
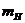 ,
, 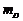 та
та 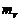
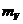 . Алгоритм вибирає піксель, для котрого мінімальним є квадрат відстані між одним з цих пікселів та колом, тобто мінімум з[1]
. Алгоритм вибирає піксель, для котрого мінімальним є квадрат відстані між одним з цих пікселів та колом, тобто мінімум з[1]
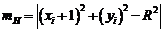
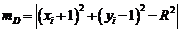
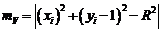
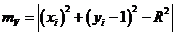
Обчислення можна спростити, якщо зауважити, що в околиці точки 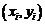
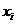
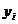 можливі тільки п’ять типів перетинів кола та сітки растру, які наведені на рис. 3.4.
можливі тільки п’ять типів перетинів кола та сітки растру, які наведені на рис. 3.4.

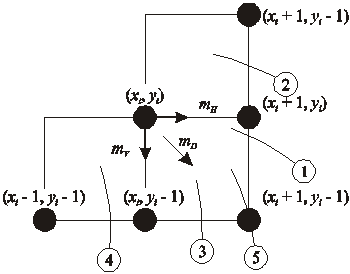
Рис. 3.4. Перетин кола та сітки растру
Різниця між квадратами відстаней від центру кола до діагоналей піксела 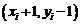
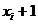
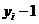 та від центру до точки на колі
та від центру до точки на колі 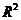 дорівнює
дорівнює
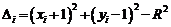
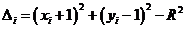
Як і в алгоритмі Брезенхема для відрізка, для вибору відповідного піксела бажано використовувати тільки знак похибки, а не її величину.
При 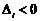 діагональна точка
діагональна точка 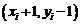
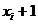
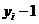 знаходиться в середині реального кола, тобто це випадки 1 або 2 на рис. 3.4. Ясно, що в цій ситуації треба вибрати або піксель
знаходиться в середині реального кола, тобто це випадки 1 або 2 на рис. 3.4. Ясно, що в цій ситуації треба вибрати або піксель 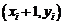
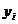 , тобто
, тобто 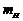
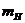 , або піксель
, або піксель 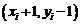
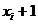
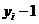 , тобто
, тобто 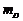
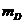 . Для цього спочатку розглянемо випадок 1 і перевіримо різницю квадратів відстаней від кола до пікселів в горизонтальному і діагональному напрямках:
. Для цього спочатку розглянемо випадок 1 і перевіримо різницю квадратів відстаней від кола до пікселів в горизонтальному і діагональному напрямках:
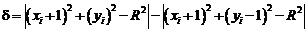
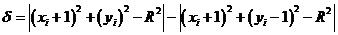
При 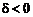 відстань від кола до діагонального піксела
відстань від кола до діагонального піксела 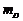
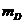 є більшою, ніж до горизонтального
є більшою, ніж до горизонтального 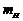
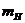 . Навпаки, якщо
. Навпаки, якщо 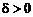
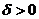 , то відстань до горизонтального піксела
, то відстань до горизонтального піксела 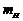
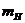 є більшою. Таким чином
є більшою. Таким чином
при 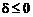 вибираємо
вибираємо 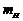
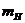 в
в 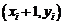
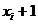
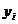
при 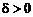
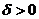 вибираємо
вибираємо 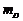
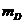 в
в 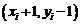
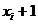
При 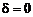 , коли відстань від кола до обох пікселів однакова, вибираємо горизонтальний крок.
, коли відстань від кола до обох пікселів однакова, вибираємо горизонтальний крок.
Кількість обчислень, яка необхідна для оцінки величини 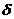 , можна скоротити, якщо зауважити, що у випадку 1
, можна скоротити, якщо зауважити, що у випадку 1
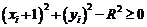
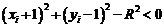
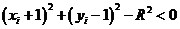
оскільки діагональний піксель 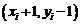 завжди лежить всередині кола, а горизонтальний
завжди лежить всередині кола, а горизонтальний 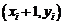
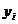 — поза ним. Отже,
— поза ним. Отже, 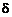 можна обчислити за формулою
можна обчислити за формулою
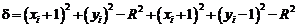
Доповнення до повного квадрату члена 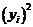
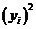 за допомогою додавання та віднімання
за допомогою додавання та віднімання 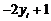
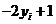 дає
дає
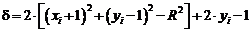
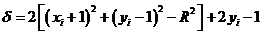
В квадратних дужках стоїть за означенням 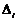
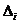 і його підставляння
і його підставляння
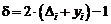
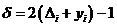
суттєво спрощує вираз.
Розглянемо випадок 2 на рис. 3.4 і зауважимо, що тут повинен бути вибраний горизонтальний піксель 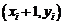
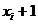
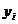 , оскільки y є монотонно спадаючою функцією. Перевіряння компонентів
, оскільки y є монотонно спадаючою функцією. Перевіряння компонентів 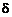 показує, що
показує, що
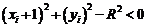
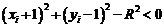
оскільки у випадку 2 горизонтальний 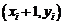 та діагональний
та діагональний 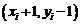 піксели лежать всередині кола. Отже,
піксели лежать всередині кола. Отже, 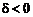 , і при використанні того самого критерію, що і у випадку 1, вибирається піксель
, і при використанні того самого критерію, що і у випадку 1, вибирається піксель 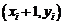 .
.
Якщо 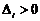 , то діагональна точка
, то діагональна точка 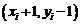 знаходиться поза колом, тобто це випадки 3 і 4 на рис. 3.4. В даній ситуації ясно, що повинен бути вибраний або піксель
знаходиться поза колом, тобто це випадки 3 і 4 на рис. 3.4. В даній ситуації ясно, що повинен бути вибраний або піксель 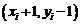 , тобто
, тобто 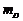 , або
, або  , тобто
, тобто 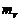 . Аналогічно розгляду попереднього випадку критерій вибору можна отримати, розглядаючи спочатку випадок 3 та перевіряючи різницю між квадратами відстаней від кола до діагонального
. Аналогічно розгляду попереднього випадку критерій вибору можна отримати, розглядаючи спочатку випадок 3 та перевіряючи різницю між квадратами відстаней від кола до діагонального 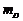 та вертикального
та вертикального 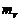 пікселів, тобто
пікселів, тобто
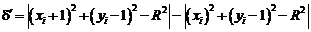
При 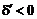 відстань від кола до вертикального піксела
відстань від кола до вертикального піксела  є більшою і необхідно вибрати діагональний крок
є більшою і необхідно вибрати діагональний крок 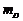 , до піксела
, до піксела 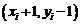 . Навпаки у випадку
. Навпаки у випадку 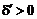 відстань від кола до діагонального піксела є більшою і необхідно вибрати вертикальний рух до піксела
відстань від кола до діагонального піксела є більшою і необхідно вибрати вертикальний рух до піксела  . Таким чином,
. Таким чином,
при 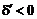 вибираємо
вибираємо 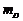 в
в 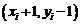
при 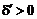 вибираємо
вибираємо 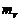 в
в 
Тут у випадку 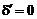 , тобто коли відстані є рівними, вибирається діагональний крок.
, тобто коли відстані є рівними, вибирається діагональний крок.
Перевірка компонент 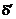 показує, що
показує, що
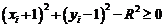
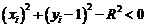
оскільки для випадку 3 діагональний піксель 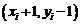 знаходиться поза колом, тоді як вертикальний піксель
знаходиться поза колом, тоді як вертикальний піксель  лежить всередині нього. Це дозволяє записати
лежить всередині нього. Це дозволяє записати 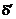 у вигляді
у вигляді

Доповнення до повного квадрату члена 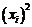 з допомогою додавання і віднімання
з допомогою додавання і віднімання 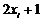 дає
дає
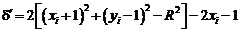
Використання визначення 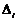 приводить вираз до вигляду
приводить вираз до вигляду
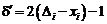
Тепер, розглядаючи випадок 4 знову зауважимо, що необхідно вибрати вертикальний піксель 
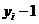 , оскільки y є монотонно спадаючою функцією при зростанні x.
, оскільки y є монотонно спадаючою функцією при зростанні x.
Перевірка компонент 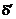 для випадку 4 показує, що
для випадку 4 показує, що
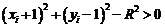
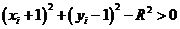
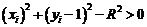
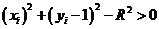
оскільки обидва піксели знаходяться поза колом. Отже, 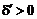
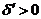 і при використанні критерію, розробленого для випадку 3, відбувається правильний вибір
і при використанні критерію, розробленого для випадку 3, відбувається правильний вибір 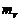
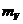 .
.
Залишилось перевірити тільки випадок 5 на рис. 3.4, який зустрічається коли діагональний піксель 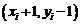
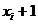 лежить на колі, тобто
лежить на колі, тобто 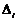
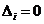 . Перевірка компонент
. Перевірка компонент 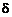 показує, що
показує, що
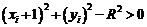
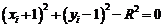
Отже, 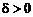
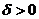 і вибирається діагональний піксель
і вибирається діагональний піксель 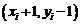
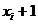 . Аналогічним чином оцінюємо компоненти
. Аналогічним чином оцінюємо компоненти 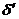 :
:
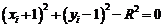
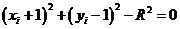
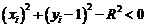
і 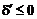
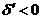 , що є умовою вибору правильного діагонального кроку до
, що є умовою вибору правильного діагонального кроку до 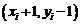 . Таким чином, випадок
. Таким чином, випадок 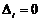
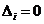 підпадає під той же критерій, що і випадок
підпадає під той же критерій, що і випадок 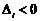 або
або 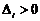
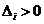 .
.
Підведемо підсумок отриманих результатів:
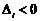
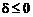
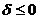 вибираємо піксель
вибираємо піксель 
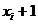
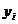
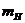
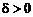
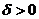 вибираємо піксель
вибираємо піксель 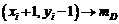
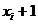
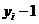
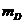
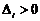
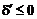
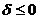 вибираємо піксель
вибираємо піксель 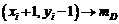
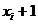
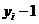
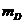
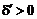
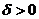 вибираємо піксель
вибираємо піксель 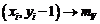
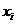
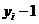
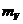
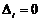 вибираємо піксель
вибираємо піксель 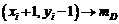
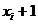
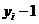
Легко розробити прості рекурентні співвідношення для реалізації покрокового алгоритму. Спочатку розглянемо горизонтальний крок 
 до піксела
до піксела 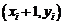
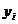 . Позначимо це нове положення піксель як
. Позначимо це нове положення піксель як 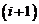
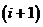 . Тоді координати нового піксела і значення
. Тоді координати нового піксела і значення 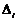 дорівнюють
дорівнюють
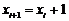
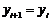
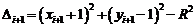


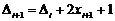
Аналогічно координати нового піксела і значення 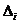 для кроку
для кроку 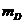 до піксела
до піксела 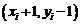 є наступними:
є наступними:
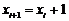
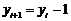
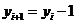
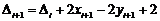
Те саме для кроку 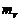
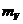 до
до 
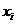
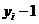
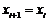
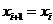
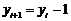
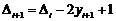
Реалізація алгоритму Брезенхема на псевдокоді для кола наведена нижче.
Покроковий алгоритм Брезенхема для генерування кола в першому квадр а нті
всі змінні — цілі
ініціалізація змінних
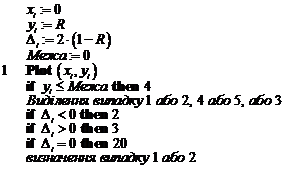
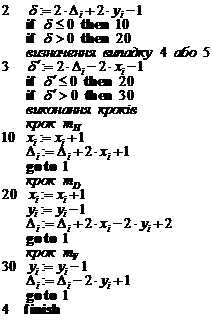

Рис. 3.5. Блок-схема покрокового алгоритму Брезенхема генерування кола в першому квадранті
Змінна межі встановлюється на нуль для закінчення роботи алгоритму на горизонтальній осі, в результаті генерується коло в першому квадранті. Якщо потрібен лише один з октантів, то другий октант можна отримати за допомогою встановлення  , а перший — за допомогою відображення другого октанту відносно прямої
, а перший — за допомогою відображення другого октанту відносно прямої 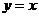 (рис. 3.1). Блок-схема алгоритму наведена на рис. 3.5.
(рис. 3.1). Блок-схема алгоритму наведена на рис. 3.5.
Приклад 3 .1. Алгоритм Брезенхема для кола
Для ілюстрації роботи алгоритму генерування кола розглянемо коло радіусом 8 з центром в початку координат. Генерується тільки перший квадрант. початкові установки покрокове виконання основного циклу ¼ Результати всіх послідовних проходів алгоритму зведені в таблицю. Список пікселів, вибраних алгоритмом, складається з (0, 8), (1, 8), (2, 8), (3, 7), (4, 7), (5, 6), (6, 5), (7, 4), (7, 3), (8, 2), (8, 1), (8, 0). Результати показано на рис. 3.6 разом з реальним колом. Алгоритм легко узагальнюється для інших квадрантів або дуг кіл. Рис. 3.6. Результати роботи покрокового алгоритму Брезенхема для генерування кола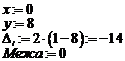
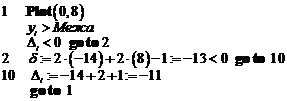
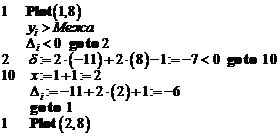
Plot

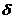
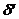
x
y
-14
(0, 8)
-11
-13
(1, 8)
-6
-7
(2, 8)
-12
(3, 7)
-3
-11
(4, 7)
-3
(5, 6)
(6, 5)
-11
(7, 4)
(7, 3)
-7
(8, 2)
(8, 1)
(8, 0)
алгоритм завершено
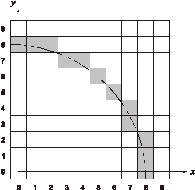
Радіус кола дорівнює 8
Підсвічені піксели
Date: 2015-07-27; view: 539; Нарушение авторских прав