
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Ряды комплексных функций и их свойства. Примеры
|
|
Напомним простейшие понятия, связанные с рядами.
Ряд из комплексных чисел
с₀+с₁+…+cn +…= 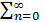 cn, (1)
cn, (1)
где cn =an + ibn, называется сходящимся, если последовательность его частичных сумм
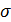 n =
n = 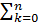 ck
ck
имеет конечный предел 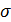 . Этот предел называется суммой ряда (1).
. Этот предел называется суммой ряда (1).
Ясно, что ряд (1) сходится тогда и только тогда, когда одновременно сходятся ряды
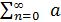 n и
n и 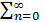 bn.
bn.
Ряд (1) называется абсолютно сходящимся, если сходится ряд из модулей
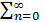 |cn|.
|cn|.
Ряды 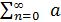 n,
n, 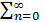 bn и
bn и 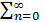 |cn|.
|cn|.
являются рядами с действительными членами, и вопрос об их сходимости решается
при помощи известных признаков сходимости рядов с действительными членами.
Функциональный ряд
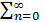 fn(z), (2)
fn(z), (2)
где функции fn(z), n = 0, 1, 2,..., определены на некотором множестве S комплексной
плоскости, называется сходящимся в точке z этого множества, если для любого
ɛ > О найдется номер N такой, что для всех n 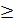 N выполняется неравенство
N выполняется неравенство
|Rn (z)| <ɛ,
где Rn (z) = 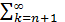 fk(z).
fk(z).
Функциональный ряд (2) называется равномерно сходящимся на множестве S, если
1) он сходится в каждой точке множества S и
2) для всякого ɛ > О найдется номер N = N(ɛ), не зависящий от z и такой, что
для всех n 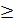 N и для всех z из S остатки этого ряда удовлетворяют неравенству
N и для всех z из S остатки этого ряда удовлетворяют неравенству
| 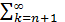 fk(z)| < ɛ.
fk(z)| < ɛ.
Точно так же, как и в случае одного действительного переменного, доказывается
важный для практических вычислений достаточный признак равномерной сходимости.
T. Признак Beйepштрасса. Пусть всюду на множестве S ряд (2) мажорируется абсолютно
сходящимся числовым рядом,
|fn(z) 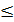 |cn|.
|cn|.
Тогда ряд (2) сходится, на множестве S абсолютно и равномерно.
На ряды функций комплексного переменного без изменений переносятся доказательства
непрерывности суммы равномерно сходящегося ряда с непрерывными членами,
теоремы о том, что равномерная сходимость функционального ряда не нарушится,
если все его члены умножить на ограниченную функцию, а также доказательство того,
что равномерно сходящийся на кусочно-гладкой кривой ряд из непрерывных функций
можно почленно интегрировать вдоль этой кривой,
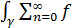 n(ζ)dζ=
n(ζ)dζ= 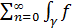 n(ζ)dζ. (3)
n(ζ)dζ. (3)
Date: 2015-07-27; view: 419; Нарушение авторских прав