Формулы Эйлера

Для любого действительного числа 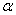справедливы следующие формулы:

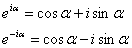
Тоже можете переписать в тетрадь в качестве справочного материала.

Строго говоря, формула всего одна, но обычно для удобства пишут и частный случай с минусом в показателе. Параметр 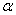не обязан быть одинокой буковкой, в качестве 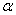может выступать сложное выражение, функция, важно лишь, чтобы они принимали только действительные значения. Собственно, мы это увидим прямо сейчас:

Пример 7

Определить действительную 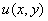и мнимую 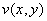части функции 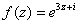. Проверить выполнение условий Коши-Римана. Найти производную.

Решение: Генеральная линия партии остаётся непоколебимой – необходимо выделить действительную и мнимую части функции. Приведу подробное решение, и ниже закомментирую каждый шаг:

Поскольку , то:

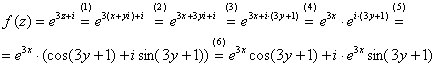
(1) Подставляем 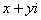вместо «зет».

(2) После подстановки нужно выделить действительную и мнимую часть сначала в показателе экспоненты. Для этого раскрываем скобки.

(3) Группируем мнимую часть показателя, вынося мнимую единицу за скобки.

(4) Используем школьное действие со степенями.

(5) Для множителя 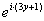используем формулу Эйлера 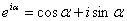, при этом .

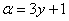(6) Раскрываем скобки, в результате:

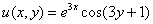– действительная часть функции ;
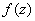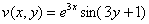– мнимая часть функции .

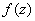Дальнейшие действия стандартны, проверим выполнение условий Коши-Римана:

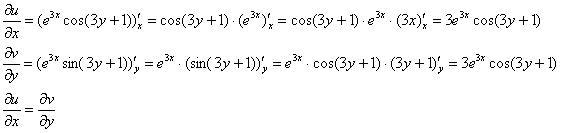
Частные производные опять не очень сложные, но на всякий пожарный расписал их максимально подробно. Проверяем второе условие:

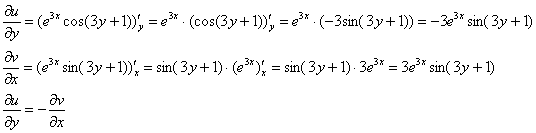
Условия Коши-Римана выполнены, найдём производную:

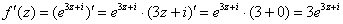
Ответ: 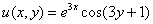, , 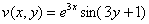условия Коши-Римана выполнены,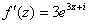

На вторую формулу Эйлера задание для самостоятельного решения:

Пример 8

Определить действительную 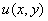и мнимую 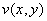части функции 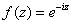. Проверить выполнение условий Коши-Римана, найти производную.

Полное решение и ответ в конце урока.
! Внимание! Знак «минус» в формуле Эйлера 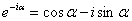относится к мнимой части, то есть 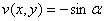. Терять минус нельзя!

Непосредственно из формул Эйлера можно вывести формулу разложения синуса и косинуса на действительную и мнимую часть. Сам вывод достаточно занудный, вот он, кстати, у меня в учебнике перед глазами (Бохан, Математический анализ, том 2). Поэтому сразу приведу готовый результат, который опять полезно переписать к себе в справочник:

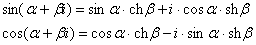
Параметры «альфа» и «бета» принимают только действительные значения, в том числе они могут быть сложными выражениями, функциями действительной переменной.

Кроме того, в формуле нарисовались гиперболические функции, при дифференцировании они превращаются друг в друга, не случайно я включил их в таблицу производных.

Пример 9

Определить действительную 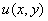и мнимую 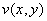части функции . Проверить выполнение условий Коши-Римана. Производную, так и быть, находить не станем.

Решение: Алгоритм решения очень похож на предыдущие два примера, но есть очень важные моменты, поэтому начальный этап я опять закомментирую пошагово:

Поскольку , то:

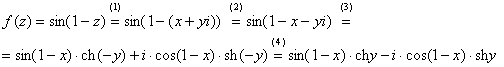
1) Подставляем 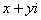вместо «зет».

(2) Сначала выделяем действительную и мнимую часть внутри синуса. В этих целях раскрываем скобки.

(3) Используем формулу 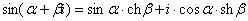, при этом .

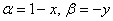(4) Используем чётность гиперболического косинуса: 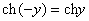и нечётность гиперболического синуса: 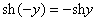. Гиперболики, хоть и не от мира сего, но во многом напоминают аналогичные тригонометрические функции.

В итоге:
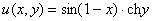– действительная часть функции ;
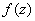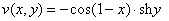– мнимая часть функции .

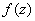Внимание! Знак «минус» относится к мнимой части, и его ни в коем случае не теряем! Для наглядной иллюстрации полученный выше результат можно переписать так:

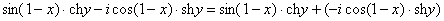
Проверим выполнение условий Коши-Римана:

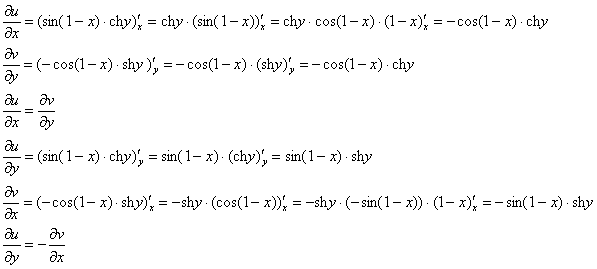
Условия Коши-Римана выполнены.

Ответ: 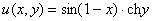, , 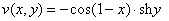условия Коши-Римана выполнены.

С косинусом, дамы и господа, разбираемся самостоятельно:

Пример 10

Определить действительную 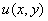и мнимую 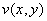части функции . Проверить выполнение условий Коши-Римана.

Я специально подобрал примеры посложнее, поскольку с чем-нибудь вроде 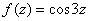все справятся, как с очищенным арахисом. Заодно внимание потренируете! Орехокол в конце урока.

Ну и в заключение рассмотрю ещё один интересный пример, когда комплексный аргумент находится в знаменателе. Пару раз в практике встречалось, разберём что-нибудь простое. Эх, старею…

Пример 11

Определить действительную 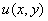и мнимую 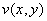части функции 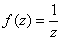. Проверить выполнение условий Коши-Римана.

Решение: Снова необходимо выделить действительную и мнимую часть функции.
Если , то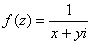

Возникает вопрос, что же делать, когда «зет» находится в знаменателе?

Всё бесхитростно – поможет стандартный приём умножения числителя и знаменателя на сопряженное выражение, он уже применялся в примерах урока Комплексные числа для чайников. Вспоминаем школьную формулу 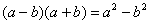. В знаменателе у нас уже есть , значит, сопряженным выражением будет 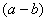. Таким образом, нужно умножить числитель и знаменатель на :

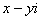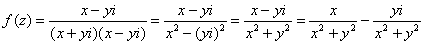
Вот и всё, а вы боялись:
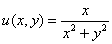– действительная часть функции ;
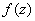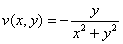– мнимая часть функции .

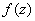Повторюсь в третий раз – не теряем минус у мнимой части!!!

Проверим выполнения условий Коши-Римана. Надо сказать, частные производные здесь не то чтобы о-го-го, но уже не из простейших:

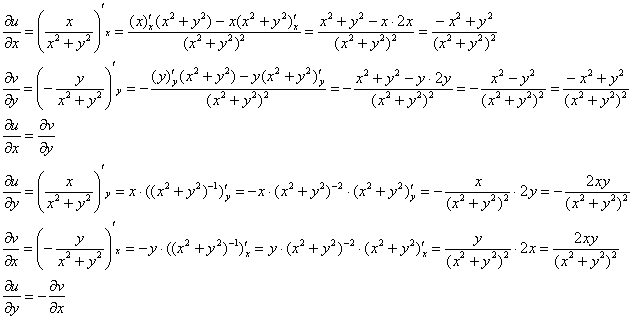
Условия Коши-Римана выполнены.

Ответ: 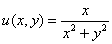, , 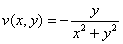условия Коши-Римана выполнены.

В качестве эпилога короткая история про ступор, или о том, какие вопросы преподавателей являются самыми сложными. Самые сложные вопросы, как ни странно – это вопросы с очевидными ответами. А история такова: сдаёт человек экзамен по алгебре, тема билета: «Следствие основной теоремы алгебры». Экзаменатор слушает-слушает, а потом вдруг спрашивает: «А откуда это следует?». Вот это был ступор, так ступор. Вся аудитория уже угорала, но студент так и не сказал правильного ответа: «из основной теоремы алгебры».

Вспоминаю историю и из личного опыта, сдаю физику, что-то там про давление жидкости, что уже не помню, но рисунок остался в памяти навсегда – изогнутая труба, по которой текла жидкость. Ответил я билет «на отлично», причем даже сам понял, что ответил. И вот преподаватель напоследок спрашивает: «Где здесь трубка тока?». Крутил-вертел я этот чертёж с изогнутой трубой минут пять, высказывал самые дикие версии, пилил трубу, рисовал какие-то проекции. А ответ был прост, трубка тока – это вся труба.

Неплохо разгрузились, до встречи на уроке Как найти функцию комплексной переменной? Там разобрана обратная задача.

Иногда очевидное – это самое сложное, всем желаю не тормозить!

Решения и ответы:

Пример 2: Решение: так как , то:

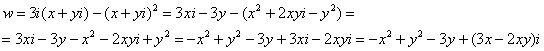
Ответ: 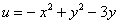– действительная часть, 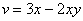– мнимая часть.

Пример 4: Решение: Так как , то:

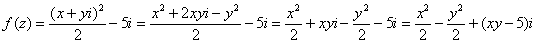
Таким образом:
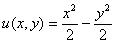– действительная часть функции ;
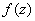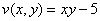– мнимая часть функции .
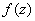Проверим выполнение условий Коши Римана:

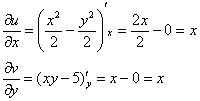
Условие 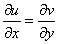выполнено.

Условие 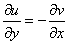также выполнено.
Условия Коши-Римана выполнены, найдём производную:

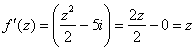
Ответ: 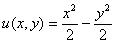– действительная часть, 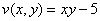– мнимая часть.
Условия Коши-Римана выполнены, .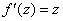

Пример 6: Решение: определим действительную и мнимую части данной функции.
Так как , то:

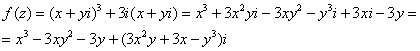
Таким образом:
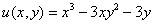– действительная часть функции ;
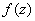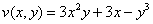– мнимая часть функции .
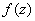Проверим выполнение условий Коши-Римана:


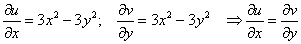
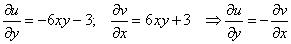
Условия Коши-Римана выполнены.


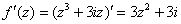
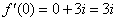
Ответ: 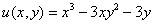, , 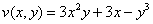условия Коши-Римана выполнены,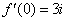

Пример 8: Решение: Так как , то:

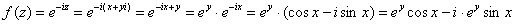
Таким образом:
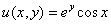– действительная часть функции ;
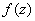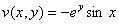– мнимая часть функции .
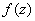Проверим выполнение условий Коши-Римана:

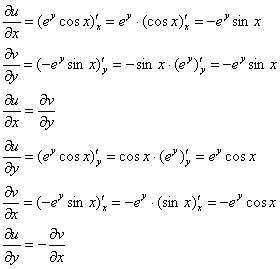
Условия Коши-Римана выполнены, найдём производную:

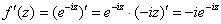
Ответ: 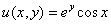, , 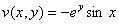условия Коши-Римана выполнены,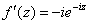

Пример 10: Решение: Так как , то:

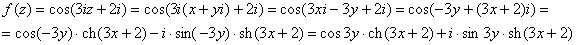
Таким образом:
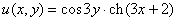– действительная часть функции ;
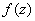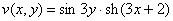– мнимая часть функции .
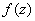Проверим выполнение условий Коши-Римана:

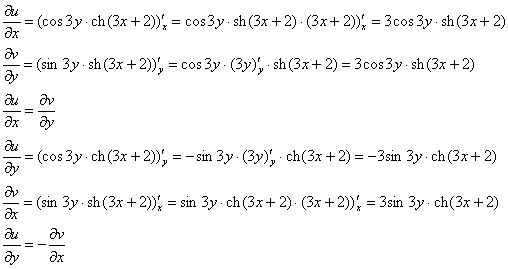
Условия Коши-Римана выполнены.
Ответ: 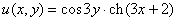, , 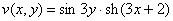условия Коши-Римана выполнены.

Автор: Емелин Александр

Date: 2015-07-27; view: 1589; Нарушение авторских прав