Действительная и мнимая часть функции комплексной переменной

Функцию комплексной переменной можно записать в виде:
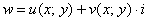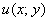, где и 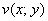– две функции двух действительных переменных.

Функция 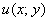называется действительной частью функции .
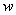Функция 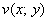называется мнимой частью функции .

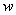То есть, функция комплексной переменной 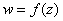зависит от двух действительных функци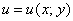й и 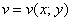. Чтобы окончательно всё прояснить рассмотрим практические примеры:

Пример 1

Найти действительную и мнимую часть функции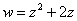

Решение: Независимая переменная «зет», как вы помните, записывается в виде , поэтому:

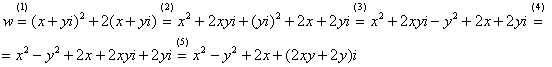
(1) В исходную функцию 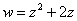подставили .

(2) Для первого слагаемого использовали формулу сокращенного умножения 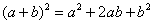. В слагаемом 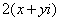– раскрыли скобки.

(3) Аккуратно возвели в квадрат 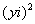, не забывая, что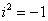

(4) Перегруппировка слагаемых: сначала переписываем слагаемые, в которых нет мнимой единицы (первая группа), затем слагаемые, где есть 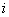(вторая группа). Следует отметить, что перетасовывать слагаемые не обязательно, и данный этап можно пропустить (фактически выполнив его устно).

(5) У второй группы выносим 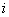за скобки.

В результате наша функция оказалась представлена в виде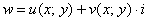

Ответ:
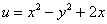– действительная часть функции .
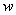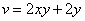– мнимая часть функции .

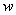Что это получились за функции? Самые что ни на есть обыкновенные функции двух переменных, от которых можно найти такие популярные частные производные. Без пощады – находить будем. Но чуть позже.

Кратко алгоритм прорешанной задачи можно записать так: в исходную функцию подставляем , проводим упрощения и делим все слагаемые на две группы – без мнимой единицы (действительная часть) и с мнимой единицей (мнимая часть).

Пример 2

Найти действительную и мнимую часть функции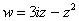

Это пример для самостоятельного решения. Перед тем как с шашками наголо броситься в бой на комплексной плоскости, позвольте дать самый важный совет по теме:

БУДЬТЕ ВНИМАТЕЛЬНЫ! Внимательным нужно быть, конечно, везде, но в комплексных числах следует быть внимательным, как никогда! Помните, что 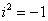, аккуратно раскрывайте скобки, ничего не теряйте. По моим наблюдениям, самой распространенной ошибкой является потеря знака. Не спешите!

Полное решение и ответ в конце урока.

Чтобы дальше легче жилось, обратим внимание на пару полезных формул. В Примере 1 было выяснено, что .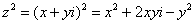

Теперь куб. Используя формулу сокращенного умножения 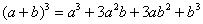, выведем:
.

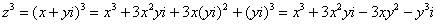Рекомендую переписать в тетрадь две рабочие формулы:

Формулы очень удобно использовать на практике, поскольку они значительно ускоряют процесс решения.

Date: 2015-07-27; view: 864; Нарушение авторских прав