
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

ТЕМА 9. Функции нескольких переменных
|
|
Множество всех упорядоченных пар действительных чисел 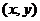 называется координатной плоскостью. Каждая точка на ней характеризуется парой своих координат. Координатная плоскость называется евклидовой плоскостью, если расстояние между двумя любыми точками
называется координатной плоскостью. Каждая точка на ней характеризуется парой своих координат. Координатная плоскость называется евклидовой плоскостью, если расстояние между двумя любыми точками 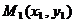 и
и 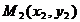 определено по формуле
определено по формуле 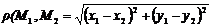 . Аналогично вводится и понятие евклидова пространства. Каждая точка координатного пространства характеризуется тройкой чисел.
. Аналогично вводится и понятие евклидова пространства. Каждая точка координатного пространства характеризуется тройкой чисел.
Множество всевозможных упорядочных совокупностей действительных чисел 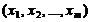 называется
называется 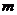 -мерным координатным пространством
-мерным координатным пространством 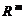 . Координатное пространство
. Координатное пространство 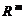 называется
называется 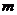 -мерным евклидовым пространством
-мерным евклидовым пространством 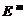 , если между двумя любыми точками
, если между двумя любыми точками 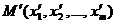 и
и 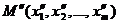 пространство
пространство 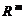 определено расстояние
определено расстояние 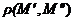 по формуле
по формуле 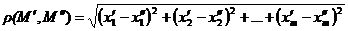 .
.
Пусть задано множество 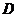 упорядоченных пар чисел
упорядоченных пар чисел 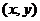 . Соответствие
. Соответствие 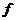 , которое каждой паре чисел
, которое каждой паре чисел 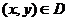 сопоставляет одно и только число
сопоставляет одно и только число 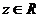 , называется функцией двух переменных, определенной на множестве
, называется функцией двух переменных, определенной на множестве 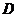 со значениями в
со значениями в 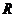 . Записывают в виде
. Записывают в виде  или
или 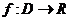 . Переменная
. Переменная 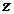 называется однозначной функцией от переменных
называется однозначной функцией от переменных 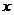 и
и 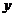 , если каждой паре значений
, если каждой паре значений 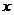 и
и 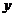 из области их изменения по некоторому правилу или закону ставится в соответствие одно определенное значение
из области их изменения по некоторому правилу или закону ставится в соответствие одно определенное значение 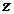 . Переменные
. Переменные 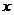 и
и 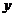 называются независимыми переменными или аргументами.
называются независимыми переменными или аргументами.
Областью определения функции  называется множество точек
называется множество точек 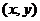 плоскости
плоскости 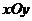 , в которых данная функция определена. Значение функции
, в которых данная функция определена. Значение функции  в точке
в точке 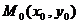 называют частным значением функции и обозначают
называют частным значением функции и обозначают 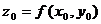 или
или 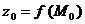 .
.
Функция двух независимых переменных также имеет геометрическое истолкование. Множество точек пространства 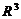 с координатами
с координатами 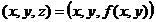 при всех
при всех 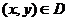 называется графиком функции
называется графиком функции  . Таким образом, каждой точке
. Таким образом, каждой точке 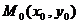 области
области 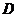 в системе координат
в системе координат 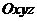 соответствует точка
соответствует точка 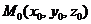 , где
, где 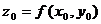 – аппликата точки
– аппликата точки 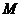 . Совокупность всех таких точек представляет собой некоторую поверхность, которая и будет геометрически изображать данную функцию
. Совокупность всех таких точек представляет собой некоторую поверхность, которая и будет геометрически изображать данную функцию  . Для наглядного геометрического представления используют линии уровня для функции двух переменных и поверхности уровня для функции трех переменных.
. Для наглядного геометрического представления используют линии уровня для функции двух переменных и поверхности уровня для функции трех переменных.
Для функции нескольких переменных вводится понятие предела и непрерывности функции аналогично случаю функции одной переменной.
Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки 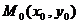 , кроме, возможно, самой этой точки. Число
, кроме, возможно, самой этой точки. Число 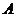 называется пределом функции
называется пределом функции  при
при 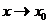 и
и 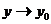 , если
, если 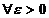
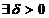 такое, что
такое, что 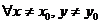 и удовлетворяющих неравенству
и удовлетворяющих неравенству 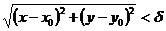 выполняется неравенство
выполняется неравенство 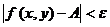 . Предел функции двух переменных обладает свойствами аналогичными свойствам предела функции одной переменной.
. Предел функции двух переменных обладает свойствами аналогичными свойствам предела функции одной переменной.
Функция  называется непрерывной в точке
называется непрерывной в точке 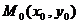 , если она определена в этой точке и некоторой ее окрестности, имеет предел
, если она определена в этой точке и некоторой ее окрестности, имеет предел 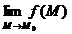 и этот предел равен значению функции
и этот предел равен значению функции 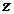 в точке
в точке 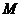 . Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Точки, в которых непрерывность нарушается, а именно не выполняется хотя бы одно из условий непрерывности функции в точке, называются точками разрыва этой функции. Точки разрыва функции
. Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Точки, в которых непрерывность нарушается, а именно не выполняется хотя бы одно из условий непрерывности функции в точке, называются точками разрыва этой функции. Точки разрыва функции  могут образовывать целые линии разрыва.
могут образовывать целые линии разрыва.
Тема 24.
Пусть функция двух переменных 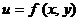 определена и непрерывна в некоторой области
определена и непрерывна в некоторой области 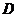 . Так как
. Так как 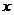 и
и 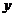 - независимые переменные, то одна из них может изменяться, а другая сохранять свое значение. Дадим аргументу
- независимые переменные, то одна из них может изменяться, а другая сохранять свое значение. Дадим аргументу 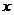 приращение
приращение 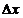 , аргументу
, аргументу 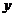 приращение
приращение 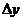 . Считаем, что точки с координатами
. Считаем, что точки с координатами 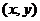 ,
, 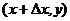 ,
, 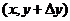 ,
, 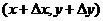 также принадлежат области
также принадлежат области 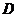 . Тогда функция
. Тогда функция 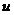 получит наращенное значение
получит наращенное значение 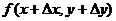 . Величина
. Величина 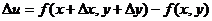 называются полным приращением функции в точке
называются полным приращением функции в точке 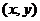 . Если задать только приращение аргумента
. Если задать только приращение аргумента 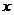 или только
или только 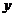 ,то полученные приращения функции соответственно равные
,то полученные приращения функции соответственно равные 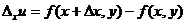 и
и 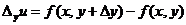 , называются частными. Полное приращение функции не равно сумме частных:
, называются частными. Полное приращение функции не равно сумме частных: 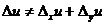 . Частной производной от функции
. Частной производной от функции 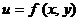 по независимой переменной
по независимой переменной 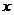 называется конечный предел
называется конечный предел 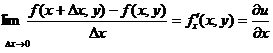 , вычисленный при постоянном значении аргумента
, вычисленный при постоянном значении аргумента 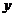 . Аналогично вводится частная производная функции
. Аналогично вводится частная производная функции 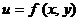 по независимой переменной
по независимой переменной 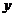 . Для частных производных справедливы правила и формулы дифференцирования функции одной переменной.
. Для частных производных справедливы правила и формулы дифференцирования функции одной переменной.
Функция  называется дифференцируемой в точке
называется дифференцируемой в точке 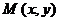 , если ее полное приращение в этой точке можно представить в виде
, если ее полное приращение в этой точке можно представить в виде 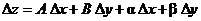 , где
, где 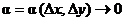 и
и 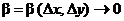 при
при 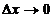 ,
, 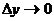 . Сумма первых двух слагаемых в равенстве представляет собой главную часть приращения функции. Главная часть приращения функции
. Сумма первых двух слагаемых в равенстве представляет собой главную часть приращения функции. Главная часть приращения функции  , линейная относительно
, линейная относительно 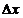 и
и 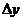 , называется полным дифференциалом этой функции
, называется полным дифференциалом этой функции 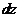 . Для независимых переменных
. Для независимых переменных 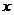 и
и 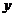
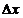 =
= 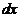 ,
, 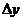 =
= 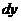 . Поэтому полный дифференциал функции
. Поэтому полный дифференциал функции  вычисляется как
вычисляется как 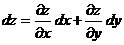 . Аналогично полный дифференциал функции трех переменных
. Аналогично полный дифференциал функции трех переменных 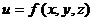
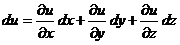 .
.
Тема 25.
Чтобы функция нескольких переменных была дифференцируема в точке, необходимо, чтобы она имела в ней частные производные, и достаточно, чтобы она обладала частными производными, непрерывными в этой точке.
Теорема (необходимое условие дифференцируемости функции): Если функция  дифференцируема в точке
дифференцируема в точке 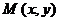 , то она непрерывна в этой точке и имеет в ней частные производные
, то она непрерывна в этой точке и имеет в ней частные производные 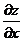 ,
, 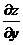 .
.
Теорема (достаточное условие дифференцируемости функции): Если функция  имеет непрерывные частные производные
имеет непрерывные частные производные 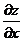 и
и 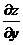 в точке
в точке 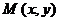 , то она дифференцируема в этой точке и ее полный дифференциал выражается как
, то она дифференцируема в этой точке и ее полный дифференциал выражается как 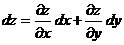 .
.
Выражение вида 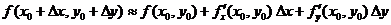 называется линеаризацией функции
называется линеаризацией функции  в окрестности точки
в окрестности точки 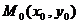 . Это соотношение применяется в приближенных вычислениях. Дифференцируемую функцию можно заменить линейной функцией в окрестности рассматриваемой точки.
. Это соотношение применяется в приближенных вычислениях. Дифференцируемую функцию можно заменить линейной функцией в окрестности рассматриваемой точки.
Частными производными второго порядка от функции  называются частные производные от ее частных производных первого порядка.
называются частные производные от ее частных производных первого порядка.
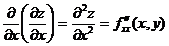 ,
, 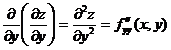 ,
,
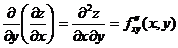 ,
, 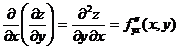 .
.
Частная производная второго и более высокого порядка, взятая по различным переменным, называется смешанной частной производной.
Теорема Шварца: Если частные производные высшего порядка непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования, равны между собой.
Полный дифференциал функции называют дифференциалом первого порядка. Пусть функция  имеет непрерывные частные производные второго порядка, а
имеет непрерывные частные производные второго порядка, а 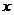 и
и 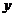 - независимые переменные. Дифференциалом второго порядка от функции
- независимые переменные. Дифференциалом второго порядка от функции  называется дифференциал от ее полного дифференциала, т.е.
называется дифференциал от ее полного дифференциала, т.е.
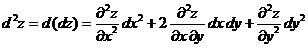 .
.
Аналогично дифференциал третьего порядка функции двух переменных  выражается
выражается
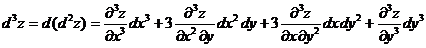 .
.
Дифференциалы высших порядков, очевидно, определяются как 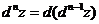
Для функций нескольких переменных имеет место инвариантность формы первого дифференциала: полный дифференциал функции  сохраняет один и тот же вид независимо от того, являются ли аргументы независимыми переменными или функциями независимых переменных.
сохраняет один и тот же вид независимо от того, являются ли аргументы независимыми переменными или функциями независимых переменных.
Тема 26.
Пусть  - функция двух переменных
- функция двух переменных 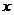 и
и 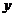 в некоторой области
в некоторой области 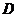 , а аргументы
, а аргументы 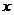 и
и 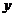 являются дифференцируемыми функциями некоторой переменной
являются дифференцируемыми функциями некоторой переменной 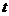 :
: 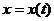 ,
, 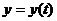 .
.
В этом случае функция 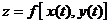 является сложной функцией одной независимой переменной
является сложной функцией одной независимой переменной 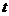 . Переменные
. Переменные 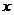 и
и 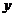 являются промежуточными переменными.
являются промежуточными переменными.
Теорема: Если  - дифференцируемая в точке
- дифференцируемая в точке 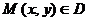 функция и
функция и 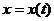 ,
, 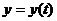 - дифференцируемые функции независимые переменной
- дифференцируемые функции независимые переменной 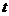 , то производная сложной функции
, то производная сложной функции 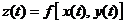 вычисляется по формуле
вычисляется по формуле 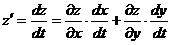 .
.
В частном случае, если 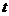 совпадает с одним из аргументов, например
совпадает с одним из аргументов, например 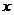 , функция
, функция 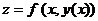 - сложная функция одной независимой переменной
- сложная функция одной независимой переменной 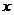 . Формула
. Формула 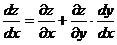 носит название формулы полной производной.
носит название формулы полной производной.
В общем случае, производная сложной функции по каждой независимой переменной равна сумме произведений частных производных этой функции по ее промежуточным переменным на их производные по соответствующей независимой переменной.
Функция  называется неявной функцией переменных
называется неявной функцией переменных 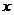 и
и 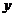 , если она определяется уравнением
, если она определяется уравнением 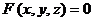 , неразрешенным относительно
, неразрешенным относительно 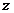 . Имеет место следующая теорема.
. Имеет место следующая теорема.
Теорема: Если функция 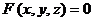 дифференцируема по переменным
дифференцируема по переменным 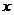 ,
, 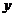 ,
, 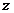 в некоторой области
в некоторой области 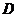 и
и 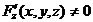 , то уравнение
, то уравнение 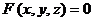 определяет однозначную неявную функцию
определяет однозначную неявную функцию  , также дифференцируемую, причем
, также дифференцируемую, причем 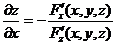 и
и 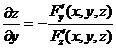 .
.
Уравнение 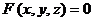 не всегда определяет одну переменную как неявную функцию двух других.
не всегда определяет одну переменную как неявную функцию двух других.
Теорема о существовании неявной функции двух переменных: Если функция 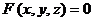 и её производные
и её производные 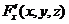 ,
, 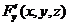 ,
, 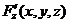 определены и непрерывны в некоторой окрестности точки
определены и непрерывны в некоторой окрестности точки 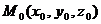 , причём
, причём 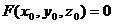 , а
, а 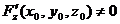 , то существует окрестность точки
, то существует окрестность точки 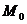 , в которой уравнение
, в которой уравнение 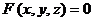 определяет единственную функцию
определяет единственную функцию  , непрерывную и дифференцируемую в окрестности точки
, непрерывную и дифференцируемую в окрестности точки 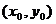 такую, что
такую, что 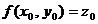 .
.
Пусть 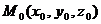 - фиксированная точка на некоторой поверхности
- фиксированная точка на некоторой поверхности 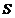 , заданной функций
, заданной функций  или уравнением
или уравнением 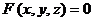 . Касательные в точке
. Касательные в точке 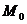 определяют некоторую плоскость, которая называется касательной плоскостью
определяют некоторую плоскость, которая называется касательной плоскостью 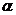 к поверхности
к поверхности 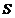 в точке
в точке 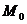 . Прямая, проходящая через точку
. Прямая, проходящая через точку 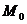 и перпендикулярная касательной плоскости, построенной в этой точке поверхности, называется ее нормалью.
и перпендикулярная касательной плоскости, построенной в этой точке поверхности, называется ее нормалью.
Тема 27.
Частные производные 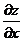 и
и 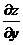 представляют собой производные от функции
представляют собой производные от функции  по двум частным направлениям осей
по двум частным направлениям осей 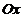 и
и 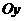 . Пусть
. Пусть  дифференцируемая функция в некоторой области
дифференцируемая функция в некоторой области 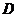 , а
, а 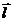 - некоторое направление, вектор с началом в точке
- некоторое направление, вектор с началом в точке 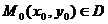 . Производной по направлению
. Производной по направлению 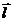 функции двух переменных
функции двух переменных  называется предел отношения приращения функции в этом направлении к величине перемещения
называется предел отношения приращения функции в этом направлении к величине перемещения 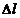 при
при 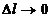 :
:
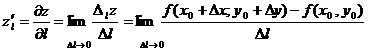 или
или 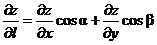 , где
, где 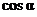 ,
, 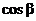 - направляющие косинусы.
- направляющие косинусы.
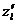 характеризует скорость изменения функции в направлении
характеризует скорость изменения функции в направлении 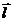 : если
: если 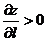 , то функция возрастает в данном направлении.
, то функция возрастает в данном направлении.
По аналогии можно определить производную по направлению для функции трех переменных.
Градиентом функции 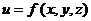 называется вектор, координатами которого являются значения частных производных функции в точке
называется вектор, координатами которого являются значения частных производных функции в точке 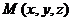 :
:
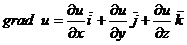 или
или 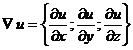
Градиент функции есть векторная величина и указывает направление наибыстрейшего возрастания функции.
| <== предыдущая | | | следующая ==> |
| Облік процесу продаж, формування та розподілу результатів господарювання | | | Импульстің сақталу заңдары |
Date: 2015-07-27; view: 353; Нарушение авторских прав