Компонентные и системные уравнения, описывающие цепь

Закономерности, описывающие поведение элементов цепи (элементные или компонентные законы)

Это математические выражения, связывающие между собой переменные, описывающие состояние элемента – токи через выводы элемента и напряжения между выводами этого элемента. Такие математические уравнения называют элементными или компонентными законами. Такие законы могут иметь вид алгебраических или дифференциальных уравнений. Количество таких уравнений для элемента с n выводами равно (n‑1).

Простейший вид элемента – с двумя выводами (двухполюсник). Его поведение описывается зависимостью между двумя величинами: i и u. Ее называют вольт-амперной характеристикой ВАХ.

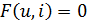Какая из переменных является независимой (аргументом) – любая.
С математической точки зрения – любая.

А с физической?

Как можно определить ВАХ экспериментально? Изменяя одну из величин и измеряя обе.

Элемент называют линейным, если ВАХ – полином первого порядка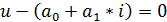

Может ли быть так, что при заданном значении аргумента 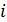функция 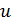не определяется однозначно?
Может ли быть так, что при постоянном значении аргумента 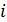функция 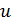не сохраняет постоянства?

Пример с конденсатором.
Пример с термозависимым резистором (саморазогрев).
Пример с диодом – нелинейный элемент

Эксперимент по снятию ВАХ резистора и полупроводникового диода а) вручную, б) с помощью характериографа

Простой вариант формирования системы компонентных уравнений для n-полюсника:

· Выбрать один из выводов в качестве базового.

· Задать величины напряжений между каждым из оставшихся и базовым выводом (возможность этого является следствием второго закона Кирхгофа).

· Измерять токи через каждый из выводов за исключением базового.

Система из (n-1) уравнений, описывающая поведение n-полюсника будет иметь вид

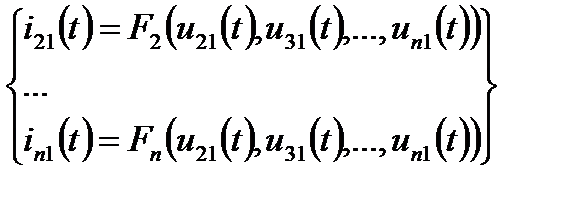
здесь F символизирует зависимость, которая может быть алгебраической, либо содержать производные и (или) интегралы переменных u(t) и i(t).

Энергетические свойства элементов электрических цепей.

Диссипативность: (необратимое) превращение электрической энергии в тепло

Переход части электрической энергии в тепло при протекании тока по диссипативным элементам. Компонентное уравнение диссипативного элемента цепи. Потери энергии в электронных информационных устройствах. Почему энергия не может быть сколь-угодно малой.

Большая группа элементов цепей обладает свойством, состоящим в том, что вся энергия, доставляемая токами, протекающими через выводы, превращается внутри таких элементов в тепло. Такие элементы называют диссипативными [2]. Примером такого элемента является резистор, используемый в электронных цепях для …??? () Компонентное уравнение диссипативного двухполюсника имеет вид

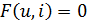(2.4)

Запись уравнения в таком виде подчёркивает тот факт, что ни одна из двух переменных 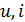не является причиной изменения другой величины, т.е. аргументом, независимой переменной, может быть любая из них. Во многих книгах утверждается (считается), что независимой переменной, причиной является изменение напряжения, в то время как изменение тока это следствие, и компонентное уравнение переписывают в виде

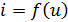(2.5)

Однако утверждение о «первичности» напряжения ошибочно.

Характеристики диссипативных элементов часто называют «вольт-амперными», поскольку в выражении присутствуют две переменные: напряжение 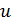и ток 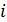. И вновь отметим, что в приведённом уравнении обе переменные могут изменяться во времени.

Вольт-амперная характеристика 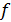может быть функцией любого вида. Так, например, у полупроводниковых диодов характеристики существенно нелинейны и весьма различны для разных типов диодов.

Для металлических проводников компонентная зависимость весьма близка к прямой пропорциональной ‑ это всем известный «закон Ома» 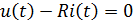, записываемый обычно в виде 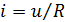. Однако при значительной величине тока вследствие саморазогрева зависимость может оказаться весьма «причудливой» (например, для нити лампы накаливания).

В электротехнических устройствах используются многочисленные элементы с числом выводов, превышающим два. Прежде всего, это транзисторы, у которых три вывода (у некоторых полевых транзисторов может быть четыре вывода). Вольт-амперные характеристики многополюсных диссипативных элементов представляют собой семейство функций нескольких аргументов. Количество функций, а также количество аргументов в каждой функции на единицу меньше количества выводов многополюсника.

Емкость: (обратимое) накопление энергии в электрическом поле (заряженного конденсатора).

Запасание части электрической энергии в реактивных элементах цепи ‑ в виде энергии электрического поля в конденсаторе или в виде энергии магнитного поля в индукторе. Компонентные уравнения реактивных элементов (накопителей энергии).

Некоторые виды элементов цепей способны обратимо накапливать электрическую энергию в электрическом или в магнитном поле.

Компонентное уравнение элемента цепи, способного накапливать энергию в электрическом поле (электростатического накопителя), в общем случае имеет вид

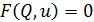(2.6)

Это соотношение иногда называют «вольт-кулонной» характеристикой. Однако при описании электрической цепи, содержащей электростатический накопитель, состояние цепи описывают, используя только напряжения и токи (и, может быть, их производные и интегралы). Этого можно достигнуть, использовав соотношение между зарядом и током (используемого в определении единицы заряда ):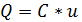

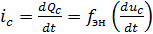(2.7)

Любой фрагмент электрической цепи, в котором имеются две точки, между которыми существует ненулевое напряжение, обладает свойствами электростатического накопителя. Вид функции 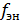зависит от свойств среды, окружающей фрагмент цепи. (Правильные, но непонятные слова). Известно более 300 веществ (сегнетоэлектрики), для которых функция 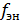существенно нелинейна.

Для большинства веществ функция 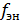имеет вид прямой пропорциональной зависимости:

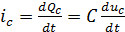(2.8)

В последней формуле 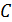– электрическая ёмкость электростатического накопителя, постоянный параметр, измеряемый в фарадах.

Изготавливаются и используются в электрических цепях конденсаторы – двухполюсники, обладающие свойством электростатического накопителя. При проектировании и изготовлении конденсаторов принимают специальные меры для обеспечения постоянства величины их емкости.

Конденсатор, заряженный до напряжения 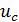(и хранящий заряд 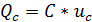) в своём электрическом поле, в соответствии с (2.1) содержит энергию 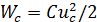. Из формулы вольт-кулонной характеристики (2.6) и (2.7) могут быть сделаны весьма важные для дальнейшего выводы:
а) скорость изменения напряжения на электростатическом накопителе тем больше, чем больше величина перезаряжающего тока,
б) напряжение на электростатическом накопителе не может измениться скачком, поскольку для этого необходим ток бесконечно большой величины, что физически не реализуемо.

Индуктивность: (обратимое) накопление энергии в магнитном поле тока.

Компонентное уравнение элемента цепи, способного накапливать энергию в магнитном поле (электромагнитного накопителя), имеет вид:

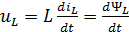(2.9)

Соотношение (2.9) иногда называют «вебер-амперной характеристикой», поскольку оно устанавливает связь между величиной суммарного магнитного потока (потокосцепления) и величиной тока, создающего этот поток. Величина потокосцепления 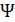измеряется в веберах, (как и магнитный поток). Коэффициент пропорциональности 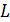называется индуктивностью и измеряется в единицах генри.

Любой фрагмент реальной электрической цепи в некоторой степени обладает свойствами магнитного накопителя, поскольку вокруг проводника с током всегда возникает магнитное поле.

Из формулы вебер-амперной характеристики (2.9) следуют важные для дальнейшего изложения выводы
а) скорость изменения тока в электромагнитном накопителе тем больше, чем больше величина напряжения между его выводами,
б) ток в магнитном накопителе не может измениться скачком, поскольку для этого напряжение между выводами магнитного накопителя должно стать бесконечно большим, что физически не реализуемо.

Для линейных двухполюсников математическое выражение этих свойств:

Резистивность (диссипативность): 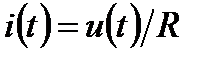и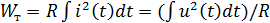
это соотношение известно как Закон Ома – ВАХ идеального резистора

Емкость электрическая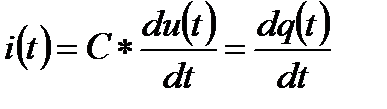
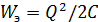
вольт-кулонная характеристика электростатического накопителя энергии

Индуктивность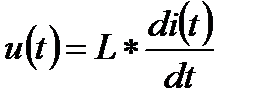
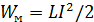
вебер-амперная характеристика электромагнитного накопителя энергии

Два последних соотношения никак не называются, хотя все три формулы представляют собой простейшие математические модели для трех видов двухполюсников: резистора, конденсатора и катушки индуктивности (индуктора).

Любой реальный двухполюсник обладает всеми тремя свойствами, только в разной степени.

В каких случаях можно пренебречь отдельными свойствами. На этот вопрос можно ответить, проведя анализ энергетического баланса.

Date: 2015-07-27; view: 2980; Нарушение авторских прав