Примеры решения задач

Пример 1. Найти интеграл .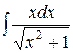

Ñ Удобно представить 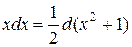. Тогда

.

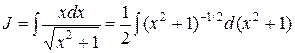Здесь . По формуле 1 таблицы имеем:

. #

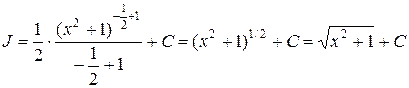Пример 2. Найти интеграл .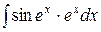

Ñ 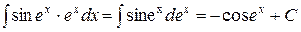. Здесь 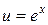, , 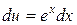использовалась формула 5. #

Пример 3. Найти интеграл .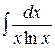

Ñ . Здесь 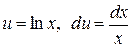, использовалась формула 2. #

Пример 4. Найти интеграл .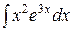

Ñ Чтобы найти этот интеграл, применим формулу интегрирования по частям:

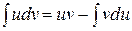(I)

Обозначим: 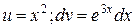. Удобно использовать следующую запись:

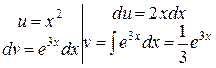
Тогда . Еще раз применим формулу (I):

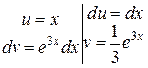
Следовательно, имеем:

. #

Пример 5. Найти интеграл .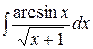

Ñ Для нахождения интеграла применим формулу (I):

. #

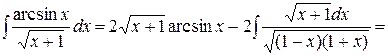
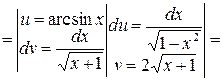
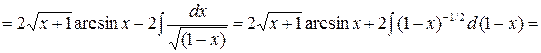
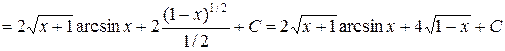Пример 6. Найти интеграл .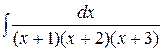

Ñ Под интегралом стоит правильная рациональная дробь. Чтобы найти этот интеграл, подынтегральную дробь нужно представить в виде суммы элементарных дробей. Это представление зависит от разложения знаменателя на множители. Корни знаменателя действительные простые, а именно x ₁ = –1, x ₂ = –2, x ₃ = –3. Тогда

.

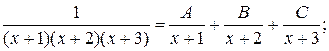
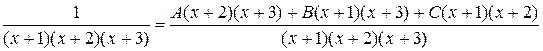Отсюда 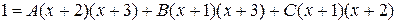. Полагая последовательно x = -1, x = -2, x = -3, получим:

. #

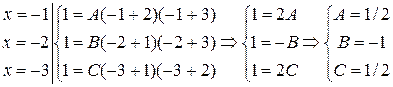
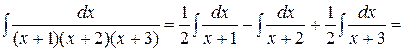
Пример 7. Найти интеграл .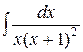

Ñ Подынтегральная функция представляет собой правильную рациональную дробь. Корни знаменателя: x ₁ = 0 – простой действительный, x ₂ = –1 – действительный кратности 2. Следовательно, разложение этой дроби на элементарные выглядит так:

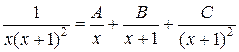
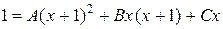(II)

Положим x = 0 и x = –1, получим два уравнения:

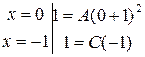
Приравнивая коэффициенты при x ² слева и справа в уравнении (II), получим и третье уравнение:

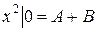
Итак, имеем систему уравнений относительно A, B, C:

. #

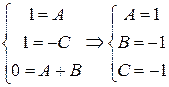
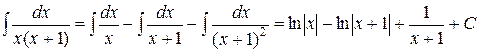Пример 8. Найти интеграл .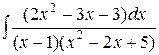

Ñ Под интегралом – правильная рациональная дробь. Знаменатель имеет следующие корни: x ₁ = 1 – простой действительный, 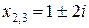– пара простых комплексных сопряженных. Подынтегральная дробь разлагается на элементарные следующим образом:

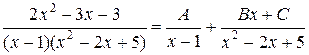
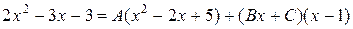(III)

Полагая x = 1 и приравнивая коэффициенты при x ² и x ⁰ слева и справа в равенстве (III), будем иметь систему уравнений:

. #

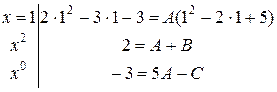
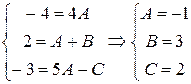
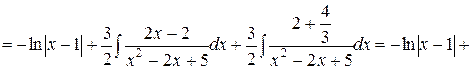
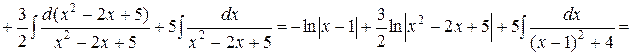
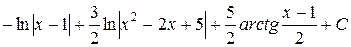Пример 9. Найти интеграл .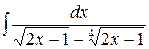

Ñ Под интегралом стоит иррациональная функция вида:

.

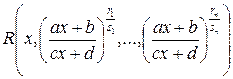Здесь a = 2; b = –1; c = 0; d = 1; 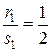; 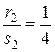. Сделаем подстановку 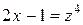, т. к. 4 – наибольший знаменатель дробе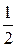й и 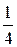, следовательно, 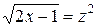, 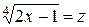. Отсюда 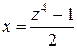, 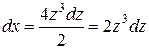. Тогда

. #

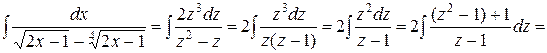
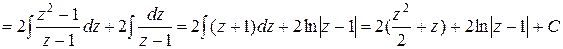
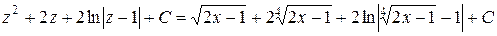Пример 10. Найти интеграл .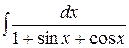

Ñ Сделаем подстановку 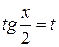, тогда , , .

. #

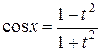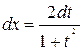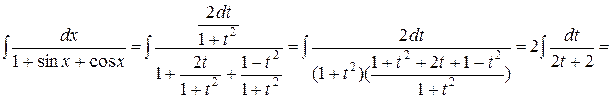
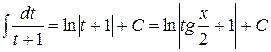Замечание: Если интеграл находится с помощью какой-либо подстановки (заменой переменной), то в конце нужно обязательно вернуться к старой переменной.

Пример 11. Вычислить несобственный интеграл или доказать его расходимость: .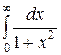

Ñ Дан несобственный интеграл I рода. Он определяется как предел соответствующего определенного интеграла:

.

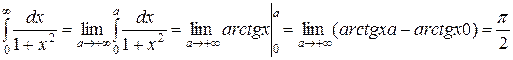Так как предел получился конечный, то интеграл сходится. #

Пример 12. Вычислить несобственный интеграл или доказать его расходимость: .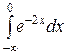

Ñ Дан несобственный интеграл I рода. Определим его как предел соответствующего определенного интеграла:

.

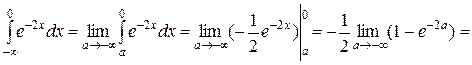
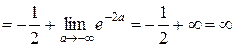Следовательно, интеграл расходится.

Пример 13. Вычислить несобственный интеграл или доказать его расходимость: .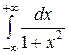

Ñ Данный несобственный интеграл определяется как сумма двух интегралов:

.

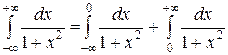Если сходятся оба интеграла, то сходится и данный интеграл. Если же хотя бы один из интегралов, стоящих справа расходится, то расходится и данный интеграл. Сходимость или расходимость данных интегралов рассмотрена в примерах 11 и 12. #

Пример 14. Вычислить несобственный интеграл или установить его расходимость: .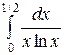

Ñ Данный интеграл является несобственным интегралом II рода, так как подынтегральная функция при 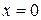является неограниченной, и определяется как предел соответствующего определенного интеграла:

.

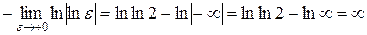Интеграл расходится. #

Пример 15. Вычислить несобственный интеграл или установить его расходимость: .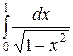

Ñ Данный интеграл является несобственным интегралом II рода, так как подынтегральная функция является неограниченной в верхнем пределе, т. е. в точке 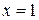. По определению

.

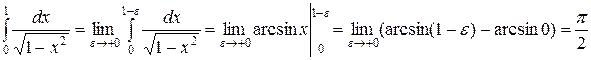Интеграл сходится. #

Пример 16. Вычислить несобственный интеграл или установить его расходимость: .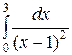

Ñ Подынтегральная функция является неограниченной в точке 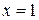, которая является внутренней для промежутка интегрирования, поэтому данный интеграл определяется как сумма двух несобственных интегралов II рода, а именно:

.

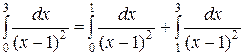Если сходятся оба интеграла, стоящие справа, то сходится и интеграл слева. Если же хотя бы один из интегралов, стоящих справа расходится, то расходится и данный интеграл. Сходимость или расходимость интегралов, аналогичных данным интегралам, рассмотрена в примерах 14 и 15. #

Пример 17. Вычислить площадь фигуры, ограниченной кривым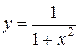и и .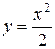

Ñ Кривая 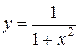(локон Аньези) расположена выше оси 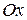, т.к. 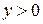для всех х. Кривая симметрична относительно оси 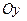: х входит в уравнение в четной степени. Наибольшее значение у будет иметь 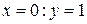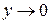при ; при .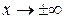

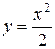– парабола с вершиной в точке (0, 0) и осью симметрии – осью 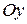. Найдем точки пересечения этих кривых, для чего решим систему уравнений:

.

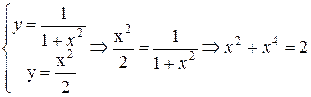Сделаем замену переменной 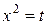, получим уравнение:

,

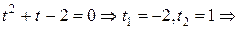
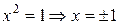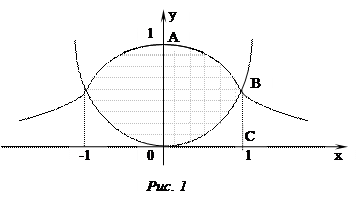Делаем чертеж фигуры (рис.1):

Фигура симметрична относительно 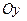, поэтому можно найти площадь S ₁, а затем ее удвоить. Площадь AOB найдем как разность площадей двух криволинейных трапеций OABC и OBC. Площадь криволинейной трапеции, заключенной между осью 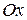, кривой 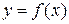и прямыми x = a и y = b находится по формуле:

.

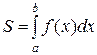В нашем случае

. #

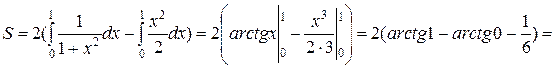
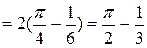Пример 18. Вычислить площадь фигуры, ограниченной кривой

.

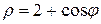Ñ Строим кривую 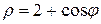. Заметим, что j может меняться от - p до p. Так как 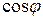– функция четная (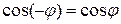), то кривая будет симметрична относительно полярной оси. Составим таблицу значений r в зависимости от j, где 0 £ j £ p:

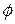
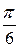
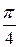
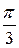
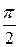
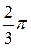
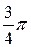
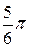
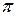
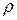
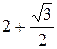
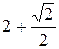
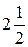
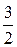
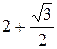
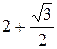
По этой таблице строим кривую (рис.2).

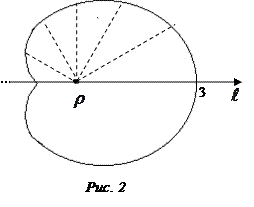
Площадь криволинейного сектора, ограниченного кривой 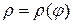и лучам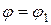и и 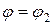, находится по формуле:

.

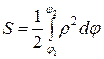Так как фигура симметрична относительно полярной оси, то площадь ее будем искать следующим образом:

. #

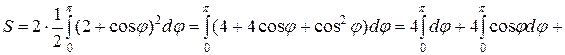
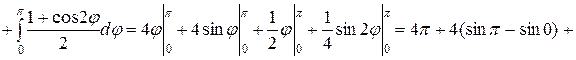
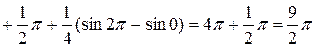Пример 19. Вычислить площадь фигуры, ограниченной кривой

.

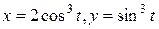Ñ Кривая является астроидой и имеет вид (рис.3):

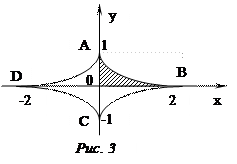Из чертежа видно, что фигура симметрична относительно осе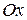й и 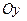, поэтому можно найти сначала 1/4 площади, а именно S_AOB, а потом найденную площадь умножить на 3. Заметим, что кривая задана параметрически в декартовой системе координат. Площадь фигуры в этом случае вычисляется по формуле:

.

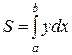Перейдем к переменной t:

,

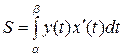где .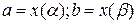

В данной задаче a = 0; b = 2; 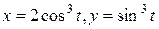; 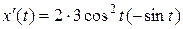. Найдем a и b.

Если .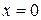

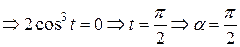Если .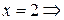

.

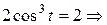
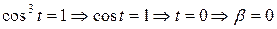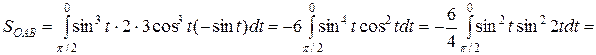
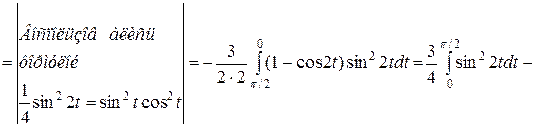
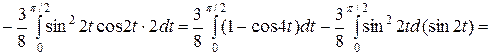
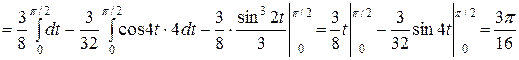Тогда площадь фигуры ABCD равна . #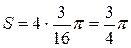

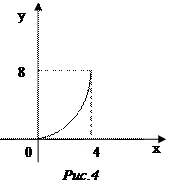
Пример 20. Вычислить длину дуги кривой 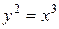от точки (0; 0) до точки (4; 8).

Ñ Длина дуги кривой, заданной в декартовой системе координат, вычисляется по формуле:

.

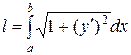Разрешим уравнение кривой относительно y:

.

. #

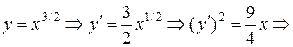
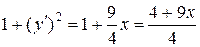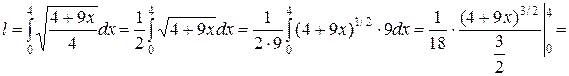
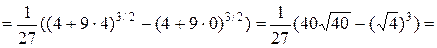
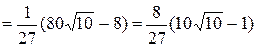Пример 21. Вычислить длину дуги развертки окружности

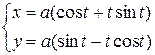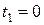от до .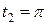

Ñ Строим кривую по точкам, для чего составим таблицу значений t, x, y.

t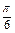
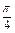
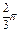
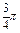
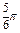
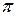
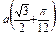
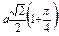
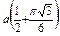
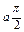
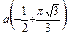
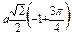
x	a								-a
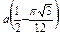
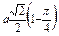
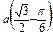
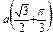
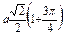
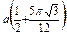
y					a				ap

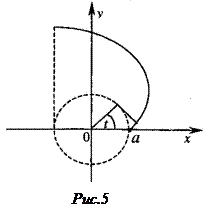Длина дуги кривой, заданной параметрически в декартовой системе координат уравнениями 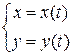, вычисляется по формуле:

.

,

.

. #

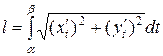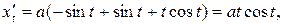
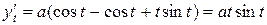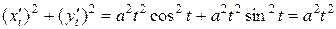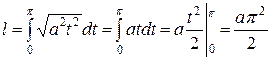Пример 22. Вычислить длину кривой от до .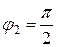

Ñ Строим кривую по точкам, для чего составим таблицу значений:

	–	–	–	–
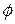
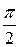
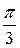
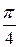
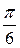
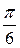
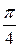
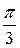
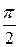
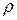
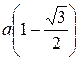
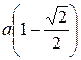
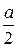
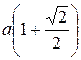
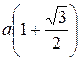
					а				2 а

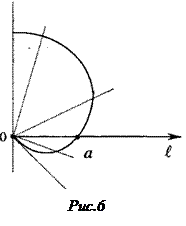
Длина дуги кривой, заданной в полярной системе координат уравнением 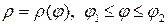, вычисляется по формуле:

.

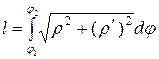В данной задаче 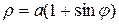Þ .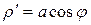

.

.

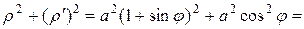
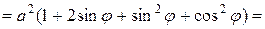
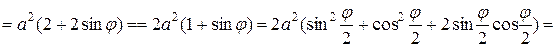
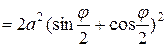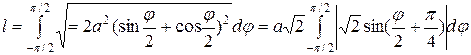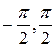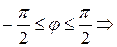
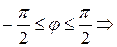
Так как пределы интегрирования , то 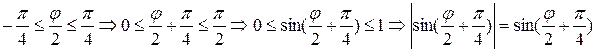. Тогда

.

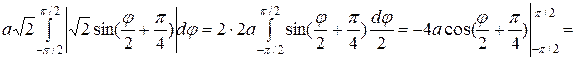
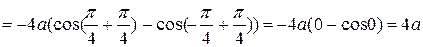Пример 23. Вычислить объем тела, образованного вращением фигуры, ограниченной одной полуволной синусоиды 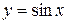и отрезком 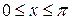оси Oх, вокруг а) оси Oх и б) оси Oy.

Ñ а) Объем тела, образованного вращением фигуры вокруг оси Ox, вычисляется по формуле:

.

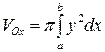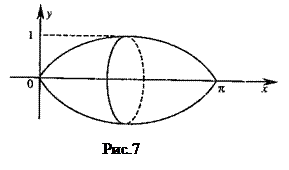
Следовательно,

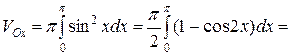
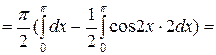
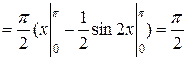
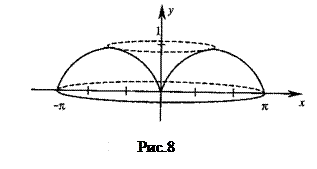б) Объем тела, образованного вращением фигуры, вокруг оси Oy, вычисляется по формуле:

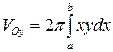
Следовательно,

. #

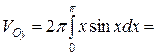
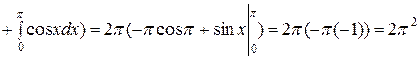Date: 2015-07-27; view: 506; Нарушение авторских прав