
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Построение экономико-математической модели
|
|
Система переменных данной экономико-математической задачи представлена основными и вспомогательной переменными. За основные переменные принимаются:
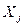 - площадь посева j -ой сельскохозяйственной культуры;
- площадь посева j -ой сельскохозяйственной культуры;
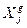 - поголовье j -го вида сельскохозяйственных животных;
- поголовье j -го вида сельскохозяйственных животных;
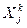 - объем приобретения j -го вида корма или кормовой добавки;
- объем приобретения j -го вида корма или кормовой добавки;
| x1 | - | Озимая пшеница товарная |
| x2 | - | Озимая пшеница фуражная |
| x3 | - | Ячмень товарный |
| x4 | - | Ячмень фуражный |
| x5 | - | Соя |
| x6 | - | Горчица |
| x7 | - | Сахарная свекла |
| x8 | - | Подсолнечник |
| x9 | - | Кукуруза на силос |
| x10 | - | Кукуруза на зеленый корм 1 срока сева |
| x11 | - | Кукуруза на зеленый корм 2 срока сева |
| x12 | - | Однолетние травы на сено |
| x13 | - | Однолетние травы на сенаж |
| x14 | - | Однолетние травы на зеленый корм 1 срока сева |
| x15 | - | Однолетние травы на зеленый корм 2 срока сева |
| x16 | - | Многолетние травы на сено |
| x17 | - | Многолетние травы на сенаж |
| x18 | - | Многолетние травы на зеленый корм |
| x19 | - | Озимые на зеленый корм |
| x20 | - | Пар |
| x21 | - | Комбикорм |
| x22 | - | Патока |
| x23 | - | Премикс |
| x24 | - | Молоко на корм |
| x25 | - | Обрат |
| x26 | - | ЗЦМ |
| x27 | - | Поголовье крупного рогатого скота |
Вспомогательная переменная (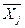 ) используется для определения суммы производственных затрат по предприятию.
) используется для определения суммы производственных затрат по предприятию.
| x28 | - | Производственные затраты |
Все условия задачи записаны в виде линейных уравнений и неравенств (ограничений), которые можно разбить на группы:
· по использованию ресурсов;
· по выполнению агротехнических требований возделывания сельскохозяйственных культур;
· по выполнению договорных обязательств по реализации продукции;
· по обеспеченности потребностей животноводства кормами собственного производства;
· по определению стоимости производственных затрат.
Основными ограничениями (с 1 по 2) являются условия, ограничивающие систему фактическим наличием ресурсов. В данном конкретном примере ограничивающими факторами будут являться площадь пашни и поголовье сельскохозяйственных животных.
В общем виде ограничение по использованию ресурсов записывается следующим образом:
 ,
,
где 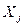 - площадь посева j -ой сельскохозяйственной культуры;
- площадь посева j -ой сельскохозяйственной культуры;
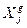 - поголовье j -го вида скота;
- поголовье j -го вида скота;
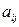 - затраты ресурсов i -го вида в расчете на 1 га посева j -ой сельскохозяйственной культуры;
- затраты ресурсов i -го вида в расчете на 1 га посева j -ой сельскохозяйственной культуры;
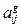 - затраты ресурсов i -го вида в расчете на 1 структурную голову j -го вида скота;
- затраты ресурсов i -го вида в расчете на 1 структурную голову j -го вида скота;
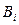 - наличие ресурсов i -го вида.
- наличие ресурсов i -го вида.
Поскольку по условиям задачи рассматривается только два вида ресурсов, то будут рассмотрены два частных случая ограничения по ресурсам
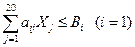 ,
,
где 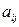 - затраты пашни в расчете на 1 га посева j -ой сельскохозяйственной культуры;
- затраты пашни в расчете на 1 га посева j -ой сельскохозяйственной культуры;
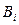 - наличие пашни в хозяйстве.
- наличие пашни в хозяйстве.
Таким образом, ограничение, гарантирующее, что площадь посева всех сельскохозяйственных культур и пара не превысит площади пашни, имеющейся в наличии, будет записано в следующем виде
1X1+1X2+1X3+1X4+……+1X17+1X18+1X19+1X20<=5600 i=1.
Коэффициенты при Xj означают, что для возделывания 1 га каждой сельскохозяйственной культуры необходимо затрачивать 1 га пашни.
Так как по условию задачи поголовье сельскохозяйственных животных должно быть сохранено на фактическом уровне, то второе основное ограничение в структурном виде записывается как:
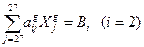 ,
,
где 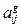 - бинарные коэффициенты связи (равны либо 0, либо 1) по i -му виду сельскохозяйственных животных;
- бинарные коэффициенты связи (равны либо 0, либо 1) по i -му виду сельскохозяйственных животных;
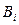 - фактическое поголовье i -го вида сельскохозяйственных животных в хозяйстве.
- фактическое поголовье i -го вида сельскохозяйственных животных в хозяйстве.
То есть сохранение существующего поголовья крупного рогатого скота обеспечивается через реализацию условия
1X27=425 i=2.
При необходимости в систему основных ограничений могут быть введены условия по использованию сенокосов, пастбищ, трудовых и других ресурсов.
Первую группу дополнительных ограничений (с 3 по 12) составляют ограничения по выполнению агротехнических требований, соблюдение которых необходимо для соблюдения научно обоснованного чередования сельскохозяйственных культур.
Эти требования представлены условиями двух видов: во-первых, по насыщению севооборота отдельными культурами или группами культур; во-вторых, по обеспечению озимых культур хорошими предшественниками.
Ограничение по насыщению севооборота отдельными культурами или группами культур в структурном виде может быть записано как
 ,
,
где Qi - верхние или нижние пределы насыщения севооборотов отдельными сельскохозяйственными культурами или группами культур.
Например, ограничение по насыщению севооборота зерновыми и зернобобовыми культурами может быть записано следующим образом:
1X1+1X2+1X3+1X4+1X5+1X19 > =2800 i=3,
1X1+1X2+1X3+1X4+1X5+1X19 <=3360 i=4.
Ограничение по насыщению севооборота озимыми:
1X1+1X2+1X19 > =1120 i=5,
1X1+1X2+1X19 <=840 i=6.
Аналогично заполняются ограничения по насыщению севооборота горчицей и соей, сахарной свеклой, подсолнечником, паром.
Информация о пределах насыщения севооборота отдельными сельскохозяйственными культурами или группами культур берется из таблицы 21 (столбцы 2 и 4).
Ограничение по обеспечению озимых культур предшественниками в структурном виде может быть записано как:
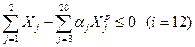 ,
,
где 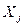 - площадь посева j -ой озимой культуры;
- площадь посева j -ой озимой культуры;
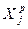 - площадь посева j -ой сельскохозяйственной культуры;
- площадь посева j -ой сельскохозяйственной культуры;
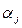 - коэффициент возможного использования посевов j -ой сельскохозяйственной культуры в качестве предшественника под озимые.
- коэффициент возможного использования посевов j -ой сельскохозяйственной культуры в качестве предшественника под озимые.
Данное ограничение может быть записано следующим образом
1X1+1X2-1X5-1X10-1X12-1X13-1X14-1X15-0,33X16-0,33X17-0,33X18-1X20<=0 i=12.
Коэффициент 0,33 при переменных, означающих многолетние травы, означает, что планируемый срок использования многолетних трав в хозяйстве составляет три года, поэтому ежегодно третья часть многолетних трав запахивается и может быть использована в качестве предшественника под озимые. Если срок эксплуатации многолетних трав будет равен четырем годам, то данный коэффициент будет равен 0,25.
Вторую группу дополнительных ограничений (с 13 по 16) составляют ограничения по выполнению договорных обязательств по реализации продукции.
Эти ограничения гарантируют, что товарной продукции по тем ее видам, на реализацию которой заключены договора, будет произведено не менее заданных объемов
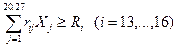 ,
,
где Xj - площадь посева j -ой сельскохозяйственной культуры или поголовье j -го вида скота;
rij - выход продукции i -го вида в расчете на 1 га посева j -ой сельскохозяйственной культуры или 1 структурную голову j -го вида скота;
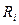 - минимально необходимый объем производства товарной продукции i- го вида.
- минимально необходимый объем производства товарной продукции i- го вида.
По условиям задачи хозяйство заключило договора на реализацию трех видов продукции: пшеницы, ячменя, сахарной свеклы и молока. Первые три ограничения будут записаны следующим образом:
30,82X1>=23000 i=13,
27,08X3>=12000 i=14,
405X7>=195000 i=15.
Ограничение по реализации молока будет иметь несколько иной вид
-1X24+51,10X27>=20000 i=16.
Поскольку потребность в молоке на корм планируется удовлетворять за счет молока собственного производства, а его объем будет определяться в ходе решения задачи, то в данном ограничении из объема валового производства молока (51,10X27) необходимо вычесть потребность в молоке на корм (X24).
Информация о выходе товарной продукции с 1 га посева соответствующих сельскохозяйственных культур берется из столбца 7 таблицы 24.
Третью группу дополнительных ограничений (с 17 по 36) составляют ограничения по обеспечению потребности отрасли животноводства в кормах. Эти ограничения гарантируют, что эти потребности будут удовлетворены как за счет собственных, так и приобретенных кормов.
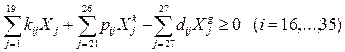 ,
,
где 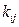 - выход корма i -го вида в расчете на 1 га посева j -ой сельскохозяйственной культуры;
- выход корма i -го вида в расчете на 1 га посева j -ой сельскохозяйственной культуры;
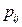 - содержание питательных веществ i -го вида в единице приобретаемого j -ого вида корма или j -ой кормовой добавки;
- содержание питательных веществ i -го вида в единице приобретаемого j -ого вида корма или j -ой кормовой добавки;
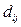 - потребность в корме i -го вида в расчете на 1 структурную голову j -ого вида сельскохозяйственных животных.
- потребность в корме i -го вида в расчете на 1 структурную голову j -ого вида сельскохозяйственных животных.
Ограничение по удовлетворению общей потребности отрасли животноводства в кормах может быть записано следующим образом
0,87X1+40,32X2+9,39X3+40,54X4+…….+0,34X24+0,13X25+2,40X26-56,14X27>=0 i=17.
По обеспечению рациона кормления переваримый протеином
0,07X1+3,34X2+0,39X3+2,70X4+…….+0,05X24+0,04X25+42,60X26-5,73X27>=0 i=18.
В ограничениях 17 и 18 информация о выходе корма (с учетом основной и побочной продукции) берется из столбцов 11 и 12 таблицы 6.
В ограничениях 20-22 и 24-25 – из столбца 11 таблицы 6. Например, ограничение по удовлетворению потребности в комбикорме запишется
1,10X21-8,47X27>=0 i=20
Ограничение по удовлетворению потребности в концентрированных кормах собственного производства будет записано как
0,87X1+40,32X2+0,71X3+31,86X4+0,36X5-6,95X27>=0 i=21.
В ограничении по соломе (23) информация о выходе соломы с 1 га посева зерновых и зернобобовых культур берется из столбца 9 таблицы 25
8,68X3+8,68X4+3,36X5-0,10X27>=0 i=23.
С помощью ограничений 26-31 происходит моделирование так называемого «зеленого конвейера», позволяющего обеспечить равномерное поступление зеленых кормов. По условиям задачи хозяйство не располагает пастбищами, поэтому выход зеленых кормов планируется только с посевных площадей соответствующих сельскохозяйственных культур.
Схема зеленого конвейера приведена в таблице 26. Например, ограничение по удовлетворению потребности в зеленых кормах в июле запишется следующим образом
23,60X15+21,10X18-0,32X27>=0 i=29.
Вспомогательным является ограничение по определению стоимости производственных затрат в целом по предприятию:
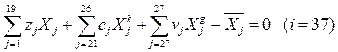 ,
,
где 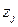 - материально-денежные затраты в расчете на 1 га посева j -ой сельскохозяйственной культуры;
- материально-денежные затраты в расчете на 1 га посева j -ой сельскохозяйственной культуры;
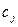 - цена приобретения j -ого вида корма или j -ой кормовой добавки;
- цена приобретения j -ого вида корма или j -ой кормовой добавки;
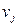 - материально-денежные затраты без учета стоимости кормов в расчете на 1 структурную голову j -ого вида сельскохозяйственных животных.
- материально-денежные затраты без учета стоимости кормов в расчете на 1 структурную голову j -ого вида сельскохозяйственных животных.
Это ограничение может быть записано следующим образом
10,10X1+10,10X2+8,50X3+8,50X4+…+0,72X21+…+23,40X27 ‑ X28=0 i=37.
Значения переменных должны быть неотрицательными
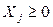 ,
, 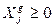 ,
,  ,
, 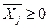
Поскольку в качестве критерия оптимальности в данной задаче выбрана максимизация сумма чистого дохода (разница между стоимостью товарной продукции и общей суммой производственных затрат по предприятию), то целевая функция примет вид:
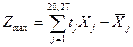 ,
,
где 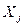 - площадь посева j -ой сельскохозяйственной культуры или поголовье j -го вида скота;
- площадь посева j -ой сельскохозяйственной культуры или поголовье j -го вида скота;
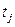 - выход товарной продукции в стоимостном выражении в расчете на 1 га посева j -ой сельскохозяйственной культуры или 1 структурную голову j -го вида скота.
- выход товарной продукции в стоимостном выражении в расчете на 1 га посева j -ой сельскохозяйственной культуры или 1 структурную голову j -го вида скота.
Целевая функция может быть записана следующим образом:
Zmax=16,68X1+12,31X3+17,64X5+19,26X6+49,50X7+20,48X8+53,27X27 ‑X28.
Таблица 8. Экономико-математическая модель по оптимизации отраслевой структуры производства (часть 1)

Продолжение таблицы 8 (часть 2).
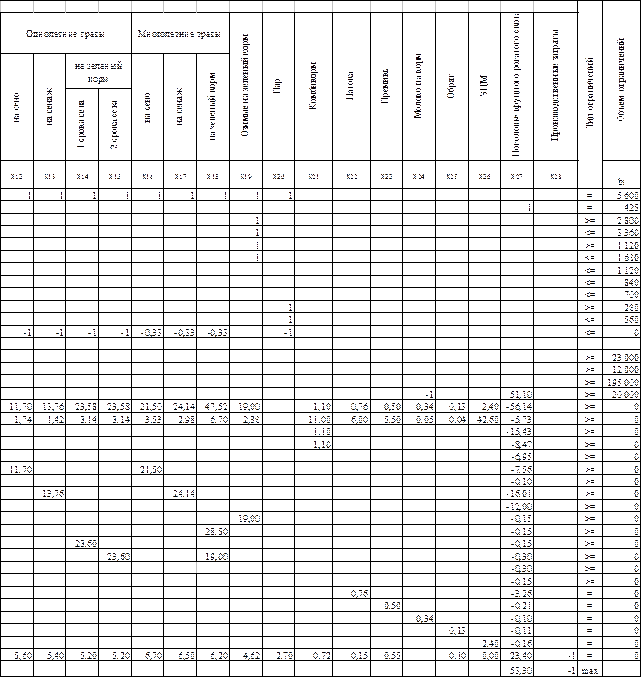
Date: 2015-07-27; view: 471; Нарушение авторских прав