Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Полное исследование функции и построение графиков
|
|
Практическая работа № 20.
Полное исследование функций. Построение графиков
Цель. Проверить знания и умения при полном исследовании функций на экстремум и построении их графиков функций.
Полное исследование функции и построение графиков
Процесс исследования функции состоит из нескольких этапов. Для наиболее полного представления о поведении функции и характере ее графика необходимо отыскать:
1) Область существования функции. Это понятие включает в себя и область значений и область определения функции.
2) Четность, нечетность. Периодичность.
3) Найти точки пересечения с осями координат, если это не вызывает затруднений.
4) Точки разрыва. (Если они имеются).
5) Интервалы возрастания и убывания.
6) Точки максимума и минимума.
7) Максимальное и минимальное значение функции на ее области определения.
8) Области выпуклости и вогнутости.
9) Точки перегиба.(Если они имеются).
10) Асимптоты.(Если они имеются).
11) Построение графика.
Пример. Исследовать функцию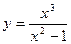 
и построить ее график.
1. D(y)= 
2.E(y)=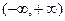 
3. 
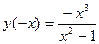- функция нечетная, график симметричен относительно начала координат, непериодичная
4. 
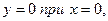
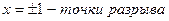
5. 
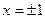- вертикальные асимптоты
Найдем наклонные асимптоты.
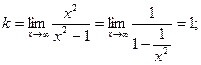
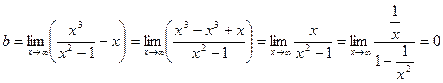
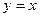- уравнение наклонной асимптоты.
6. 
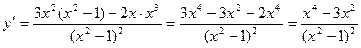
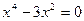
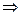
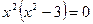
Критические точки: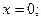 
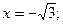
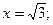
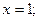
Находим промежутки возрастания и убывания функции. Для этого определяем знаки производной функции на промежутках.
-¥ < x < - 
, y¢ > 0, функция возрастает
- < x < -1, y¢ < 0, функция убывает
-1 < x < 0, y¢ < 0, функция убывает
0 < x < 1, y¢ < 0, функция убывает
1 < x < , y¢ < 0, функция убывает
< x < ¥, y¢¢ > 0, функция возрастает
7. 
.
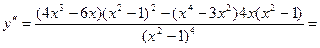
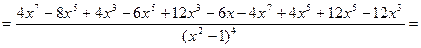
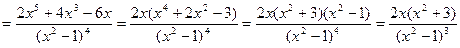Определим выпуклость и вогнутость кривой на промежутках.
-¥ < x < - , y¢¢ < 0, кривая выпуклая
- < x < -1, y¢¢ < 0, кривая выпуклая
-1 < x < 0, y¢¢ > 0, кривая вогнутая
0 < x < 1, y¢¢ < 0, кривая выпуклая
1 < x < , y¢¢ > 0, кривая вогнутая
< x < ¥, y¢¢ > 0, кривая вогнутая
Видно, что точка х = - является точкой максимума, а точка х = является точкой минимума. Значения функции в этих точках равны соответственно 3 /2 и -3 /2.
| <== предыдущая | | | следующая ==> |
| Нарощення за складною процентною ставкою | | |
Date: 2015-07-27; view: 602; Нарушение авторских прав