Прохождение света через линейные фазовые пластинки

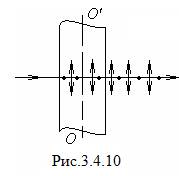Рассмотрим кристаллическую пластинку, вырезанную параллельно оптической оси OO` (рис.3.4.10), на которую падает нормально линейно-поляризованный свет, плоскость поляризации которого составляет угол j с оптической осью пластинки (обычно j =45°). В кристалле в одном и том же направлении будут распространяться две волны с разными скоростями и 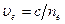, поляризованные взаимно ортогонально (рис.3.4.11). На рис.3.4.11 Р - плоскость поляризации падающего на пластинку света, 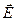- его вектор-амплитуда, OO` - оптическая ось кристалла, 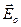и 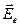- векторы-амплитуды обыкновенной и необыкновенной волн в кристаллической пластинке. А зависимости от толщины h пластинки обе волны выходят из пластинки с той или иной разностью фаз d, которая зависит от оптической разности хода данных волн, 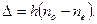Разность фаз 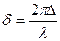, где l - длина волны в вакууме, тогда

.

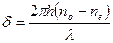Итак, из кристаллической пластинки выходят две взаимно ортогональные плоско-поляризованные волны: одна поляризована перпендикулярно к главному сечению кристалла, другая – в плоскости этого сечения (рис.3.4.11), и в произвольной точке за кристаллической пластинкой соответствующие колебания светового вектора

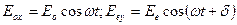. (3.4.15)

Будем считать, что оптическая разность хода обыкновенной и необыкновенной волн меньше длины когерентности, тогда обе волны будут когерентными, и разность фаз d не зависит от времени.

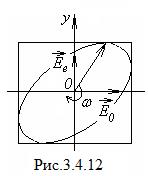
Характер поляризации результирующей волны зависит от толщины пластинки, которая и определяет разность фаз d. Уравнение (3.4.15) – это уравнение эллипса в параметрической форме, поэтому вышедший из пластинки свет оказывается эллиптически поляризованным. Результирующий вектор 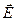вращается с угловой скоростью w, изменяясь при этом периодически по модулю (рис.3.4.12).

В зависимости от толщины пластинки h характер поляризации будет меняться. Рассмотрим некоторые частные случаи.

1. Пластинка в четверть волны. Толщина h удовлетворяет условию:

.

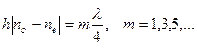Эта пластинка вносит дополнительную разность фаз 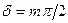, т – нечетное, между проходящими через нее обыкновенной и необыкновенной волнами. Свет, прошедший через пластинку, согласно выражению (3.4.15), оказывается эллиптически поляризован, причем эллипс приведен к осям Х и Y (рис.3.4.13). Направления вращения вектора чередуются: при т =1 – по часовой стрелке, при т =3 – против, и т.д.

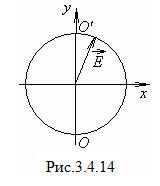Если линейно поляризованный свет падает на пластинку так, что угол между его плоскостью поляризации Р и оптической осью пластинки j =45°, то амплитуды обыкновенной и необыкновенной волн будет одинаковы, и на выходе из пластинки получается круго-поляризованный свет – эллипс вырождается в окружность (рис.3.4.14).

2. Пластинка в полволны. Ее толщина удовлетворяет условию

.

На выходе из такой пластинки между обыкновенной и необыкновенной волнами возникает разность фаз 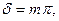где т – нечетное. Свет, вышедший из пластинки, останется линейно-поляризованным, но направление колебаний вектора 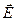(плоскость поляризации) повернется на угол 2 j симметрично главному сечению пластинки (рис.3.4.15). При j =45° такая пластинка поворачивает плоскость поляризации на 90°, т.е. плоскость поляризации прошедшего света будет ортогональна плоскости поляризации падающего света.

При четных значениях т прошедший через пластинку свет остается линейно-поляризованным в той же плоскости, что и падающий свет, т.е. такая пластинка ничего нового не вносит. Ее называют пластинкой в целую волну.

3. Компенсатор. Для анализа поляризованного света наряду с пластинкой в четверть волны используют устройства, позволяющие скомпенсировать до нуля или дополнить до p любую разность фаз между двумя взаимно ортогональными колебаниями. Их называют компенсаторы.

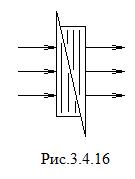
Простейший компенсатор состоит из двух кварцевых клиньев (рис.3.4.16), образующих кристаллическую пластинку, оптическая ось которой параллельна ее граням. Один из клиньев можно перемещать относительно другого при помощи микрометрического винта, изменяя таким образом толщину пластинки-компенсатора, а значит и вносимую этой системой разность фаз между обыкновенной и необыкновенной волнами.

Если на компенсатор падает нормально линейно-поляризованный свет, плоскость которого составляет угол 45° с его оптической осью, то с увеличением толщины компенсатора растет и разность фаз взаимно ортогональных волн, проходящих через него. В результате можно наблюдать картину (рис.3.4.17) изменения характера поляризации прошедшего света с ростом разности фаз d. Из рис.3.4.17 видно, что направление поляризации периодически меняется. Если сначала было правое (т.е. по часовой стрелке), то с ростом толщины пластинки-компенсатора оно переходит в левое, т.е. против часовой стрелки, и т.д.

Date: 2015-07-27; view: 1169; Нарушение авторских прав