к экзамену по эконометрике

Задание для самоподготовки

Задание 1 (0.5 балла). Для какой из выборок остатков можно принять предположение о нормальности

распределения, используя выборочные коэффициенты асимметрии и эксцесса:

А) 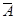= -1.45, 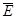= -5.85, 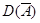= 0.8, 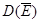= 1.2;

Б) 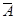= 0.21, 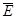= - 0.02, 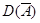= - 0.4, 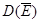= 0.8,

В) 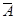= 2.9, 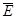= - 1.55, 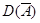= 0.3, 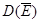= 0.7;

Г) 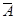= - 1.2, 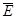= 0.75, 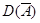= 0.5, 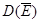= 1.1.

Задание 2 (0.5 балла). Какая из моделей линейной регрессии является более подходящей, если

объем выборки n = 25, остатки имеют нормальное распределение, не коррелированны,

гетероскедастичность отсутствует:

А) = 1.2 + 1.1 x₁ + 1.4 x₂ + 0.8 x₃, R² = 0.702; Б) = -15 – 5.7 x₂, R² = 0.115;

В) = 1.3 – 1.2 x₁ – 0.4 x₂ + 0.2 x₄ , R² = 0.215; Г) = 8 + 1.2 x₁ + 1.3 x₂, R² = 0.703.

Задание 3 (1.5 балла). При изучении зависимости y от x₁, x₂, x₃ получено четыре варианта модели.

Какая из них НЕ МОЖЕТ быть использована, если остатки имеют нормальное распределение,

гетероскедастичности нет, a = 0.05, n = 28:

А) = 4 – 0.3 x₁ – 0.7 x₂ – 0.6 x₃, R² = 0.95, D_v = 1.89,

Б) = 10 – 0.12 x₂, R² = 0.83, D_v = 2.07,

В) = 2.5 – 0.5 x₁, R² = 0.95, D_v = 3.45,

Г) Все три модели.

Указание: проверить значимость моделей по критерию Фишера, предположение Н2 МНК по критерию

Дарбина-Уотсона, сравнить R²_adj .

Задание 4 (1.5 балла). При изучении зависимости y от x₁, x₂, x₃ получено четыре варианта модели. Какая из

них МОЖЕТ быть использована и БОЛЕЕ подходит, если выполнены предположения Н1, Н3 МНК,

a = 0.05, n = 28:

А) = 2 – 0.4 x₁ – 0.7 x₂ + 0.3 x₃, R² = 0.995, D_v = 2.12,

Б) = 1 – 0.15 x₁, R² = 0.303, D_v = 2.18,

В) = 11 – 1.8 x₁ – 0.5 x₂ , R² = 0.923, D_v = 1.87,

Г) = 4 – 0.9 x₂, R² = 0.995, D_v = 3.44.

Указание: проверить значимость моделей по критерию Фишера, предположение Н2 МНК по критерию

Дарбина-Уотсона, сравнить R²_adj .

Задание 5 (0.5 балла). Если оцениваются коэффициенты линейной регрессии

y = b₀ + b₁ x₁ + b₂ x₂ + b₃ ln x₂ + e,

при объеме выборки n = 32, то число степеней свободы для критерия Стьюдента равно …….

Задание 6 (0.5 балла). Изучается линейная регрессия y = b₀ + b₁ x₁ + b₂ x₂ + e по выборке объемом n = 25.

Указать табличное значение F_α, которое будет использовано при проверке гетероскедастичности по критерию

Голдфелда-Квандта ……..

Задание 7. По данным из файла samopod.xls изучается регрессия

y = b₀ + b₁ x^0.5 + e.

Требуется:

1. Ввести новую переменную и вычислить ее значения; перейти к модели линейной регрессии,

найти оценки ее параметров; записать выборочное уравнение регрессии; проверить значимость

объясняющей переменной (2 балла);

2. Для полученной линейной модели проверить выполнение предположения H1 МНК,

используя тест Голдфелда-Квандта, α = 0.05, (2 балла);

3. Для полученной линейной модели проверить выполнение предположения Н3 МНК, используя критерий хи-квадрат, α = 0.05, (2 балла);

4. В случае выполнения предположений Н1 и Н3 МНК вычислить точечный прогноз y⁰,

если x = x⁰ = 15.0. (2 балла);

5. Если указанные предположения МНК не выполнены, обосновать невозможность

точечного прогноза (2 балла).

Date: 2015-08-15; view: 389; Нарушение авторских прав