Формулы численного дифференцирования,получение интерполяционного многочлена

Приводимые ниже формулы численного дифференцирования применяются в тех случаях, когда функция y = f (x) задана таблично (y_i = f (x_i) в равносторонних узлах 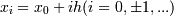). 1) 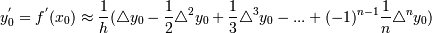(Формула применяется только для начальных строк таблицы)

2) 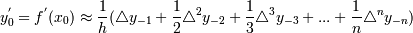(Формула применяется только для последних строк таблицы)

3) В середине таблицы применяется формула

,

полученная путем дифференцирования инерполяционного многочлена Стирлинга.

Замечание: Основным принцип численного дифференцирования заключается в следующем: поскольку любую функцию, заданную таблично можно применять интерполяционным многочленом, выбрав какое-нибудь множество из n + 1 узлов, то производную от интерполяционного многочлена 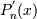можно использовать в качестве приближенного применения таблично заданной функции 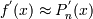. Обычно формулы численного дифференцирования применяют для нахождения производных в узлах x_i, так как при этом лубую точку можно принимать за начальную, то формулы записывают для x ₀.

Приближенные формулы нахождения производных второго порядка получается путем двукратного дифференцирования интерполяционных многочленов Ньютона и Стирлинга.

1) (для начала таблицы)

2) 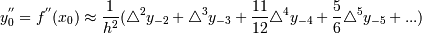(для конца таблицы)

3) 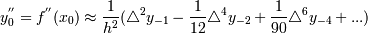(для середины таблицы)

При численном дифференцировании таблично заданной функции y = f (x) возникают погрешности двух типов:

§ погрешности усечения

§ погрешности округления

Date: 2015-08-15; view: 353; Нарушение авторских прав