Период полураспада. Когда были получены искусственные радиоактивные изотопы с малыми временами жизни, заметили, что со временем интенсивность радиоактивного излучения

Когда были получены искусственные радиоактивные изотопы с малыми временами жизни, заметили, что со временем интенсивность радиоактивного излучения уменьшается. Исследования показали, что уменьшение интенсивности излучения является следствием того, что уменьшается число распадающихся ядер. Был установлен общий для всех распадов закон - интенсивность излучения пропорциональна количеству еще нераспавшихся ядер. Этот факт позволяет получить временной закон убывания числа еще нераспавшихся ядер и, соответственно. интенсивности радиоактивного излучения.

Из факта пропорциональности интенсивности излучения числу нераспавшихся ядер вытекает экспериментально подтверждаемое следствие. Допустим, имелось первоначально N0 радиоактивных ядер. В результате распадов через время T их количество уменьшилось вдвое. Закон состоит в том, что новое число радиоактивных ядер N уменьшается вдвое также за время T. Уменьшение вдвое любого числа нераспавшихся ядер данного сорта происходит за одно и то же время T. Это время называется периодом полураспада.

Пусть первоначальное число радиоактивных ядер N0. Построим последовательность чисел выживших ядер
N0при t=0;
N0 / 2 при t=T;
N0 / 4 при t=2T;
N0 / 8 при t=3T;
×××××
N0 / 2ⁿ при t=nT.
Эта последовательность подсказывает следующий закон убывания числа нераспавшихся ядер:
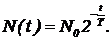(1)
Закон (1) можно представить еще в одном, наиболее часто употребляющемся виде. Заметим, что 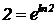, поэтому левую часть уравнения (1) можно записать в виде
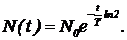(2)
Величина 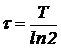равна среднему времени жизни ядра в нераспавшемся состоянии. Этот же закон управляет и распадом возбужденных состояний атома.

То, что интенсивность распада за равные промежутки времени уменьшается в равное число раз, говорит о равной вероятности распада ядра в равные малые промежутки времени вне зависимости от того, сколько ядро уже прожило. “Ядра не стареют”. Сколько бы они не прожили - вероятность распада в последующий малый интервал времени остается одной и той же. Из этого обстоятельства можно было бы вывести закон (2).

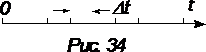Дополнительный материал. Пусть в начальный момент времени было N0 радиоактивных ядер. Определим их число в момент времени t. Разобьем интервал ( 0, t ) на равные малые промежутки времени длительности Dt. Если вероятность распада в любой промежуток времени одна и та же, то, если перед началом временного интервала было N молекул, то за время Dt их число уменьшится на DN=-NlDt, где l - постоянная, характеризующая скорость распада данных ядер. Для каждого промежутка времени можно записать
N0-N1=N0lDt;
N1-N2=N1lDt;
N2-N3=N2lDt;
×××××
Nn-1-Nn=Nn-1lDt.
Поделим обе части первого уравнения на N0, второго на N1, и т.д. Тогда система уравнений может быть переписана так:
N1 / N0=1-lDt;
N2 / N1=1-lDt;
N3 / N2=1-lDt;
×××××
Nn / Nn-1=1-lDt.
Перемножим почленно все уравнения, тогда получим
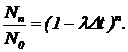(3)
Заметим, что Dt=t/n, поэтому уравнение (3) можно записать так
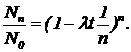(4)
Если сделать замену переменных -n/lt=m, то уравнение (4) принимает вид
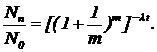(5)
Нас, конечно, интересует значение правой части уравнения (5) при 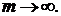Если с помощью калькулятора вычислить несколько значений выражения 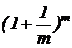при m=4, 8, 16, 32, 64, 128 и т.д., то можно заметить, что получающаяся последовательность значений этого выражения - 2,4414; 2,5658; 2,6379; 2,6770; 2,6973; 2,7077 - стремится к некоторому пределу. Этот предел равен основанию натурального логарифма - e. Таким образом, уравнение (5) приобретает вид
N(t)=N0e-lt. (6)
Сравнивая (6) с выражением (2), можно сделать вывод, что скорость распада l связана с периодом полураспада и со средним временем жизни соотношением
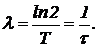(7)

Date: 2015-07-22; view: 470; Нарушение авторских прав