
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Преобразование формулы для приливообразующего потенциала
|
|
Вернемся к формуле (6.10). Здесь аргументом полиномов Лежандра является геоцентрическое зенитное расстояние притягивающего небесного тела 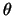 . Рассмотрим треугольник OPL. Сторона ОР, как мы знаем, равна радиусу Земного шара
. Рассмотрим треугольник OPL. Сторона ОР, как мы знаем, равна радиусу Земного шара 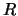 (если точка P находится на поверхности земного шара), сторона OL равна расстоянию между центрами масс притягивающего и притягиваемого тела
(если точка P находится на поверхности земного шара), сторона OL равна расстоянию между центрами масс притягивающего и притягиваемого тела 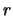 , угол между этими сторонами равен геоцентрическому зенитному расстоянию
, угол между этими сторонами равен геоцентрическому зенитному расстоянию 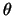 , угол между сторонами PL и продолжением стороны ОР равен зенитному расстоянию z. Проекция стороны OL на продолжение стороны ОР равна
, угол между сторонами PL и продолжением стороны ОР равен зенитному расстоянию z. Проекция стороны OL на продолжение стороны ОР равна 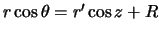 . Отсюда
. Отсюда
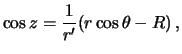
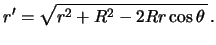
Можно ли заменить геоцентрическое зенитное расстояние топоцентрическим, которое используется в астрономии? Какую ошибку мы сделаем, если заменим в формуле (6.8) угол 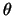 зенитным расстоянием
зенитным расстоянием 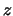 ? Очевидно, что мы должны оценить величину
? Очевидно, что мы должны оценить величину 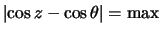
Пусть отношение 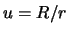 является малой величиной, тогда
является малой величиной, тогда
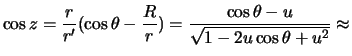
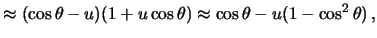
следовательно 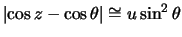 . Эта величина максимальна при
. Эта величина максимальна при 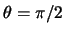 . Так если гравитирующее тело -- Луна, то
. Так если гравитирующее тело -- Луна, то 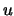 =6.371/384.4=0.0166. Следовательно, максимальное искажение зенитного расстояния в системе Земля-Луна не превосходит 1,7%. Для большинства задач этим отличием можно пренебречь и в качестве приливообразующего потенциала брать
=6.371/384.4=0.0166. Следовательно, максимальное искажение зенитного расстояния в системе Земля-Луна не превосходит 1,7%. Для большинства задач этим отличием можно пренебречь и в качестве приливообразующего потенциала брать
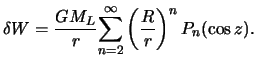
| (6.10) |
Понятно, что наибольший вклад в приливные явления создает первый член формулы (6.10). Очень часто им и ограничиваются, хотя при строгом анализе приливных явлений приходится учитывать и остальные члены разложения (6.10).
Итак, приливообразующий потенциал с точностью до  имеет вид
имеет вид
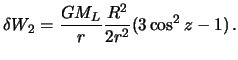
| (6.11) |
Выполним некоторые преобразования полученной формулы и приведем к общепринятому виду. Поскольку 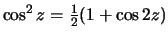 , то подставляя это выражение в формулу (6.11) осле несложных преобразований, получим
, то подставляя это выражение в формулу (6.11) осле несложных преобразований, получим
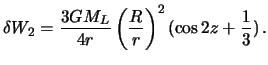
| (6.12) |
Величина 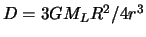 называется постоянной Дудсона. Теперь вместо (6.12) можно записать
называется постоянной Дудсона. Теперь вместо (6.12) можно записать
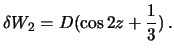
| (6.13) |
Заметим, что так называемая постоянная Дудсона вовсе не является, постоянной величиной, так как расстояние между притягивающим и притягиваемым телами изменяются из-за того что они движутся по орбитам, строго говоря, не эллиптическим, подчиняясь законам небесной механики. В книге бельгийского ученого П. Мельхиора известного специалиста по приливам приводятся численные значения постоянных Дудсона:
| для Луны | 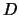 = 2,6206 м = 2,6206 м 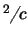 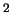 , ,
|
| для Солнца | 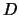 = 1,2035 м = 1,2035 м 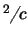 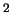 . .
|
Date: 2015-07-25; view: 566; Нарушение авторских прав