
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Объединение состояний
|
|
Во многих приложениях определение асимптотических (стационарных) значений вероятностей состояний с помощью моделей пространств состояний можно упростить, если объединить некоторые множества состояний для того, чтобы они образовали единичное совокупное состояние.
После объединения групп состояний возникает новый процесс с некоторыми новыми состояниями (совокупными состояниями) и с новыми переходами (между совокупными состояниями). В большинстве случаев новый процесс уже не будет Марковским, потому что продолжительности пребывания системы в совокупных состояниях, вообще говоря, распределены не по экспоненциальному закону.
Новый процесс останется Марковским только при удовлетворении условия объединяемости – условия, при котором интенсивности перехода к любому другому состоянию или к группе объединенных состояний одинакова для всех состояний, входящих в рассматриваемую группу. При выполнении этого условия можно рассчитать вероятности нахождения системы в любом состоянии не только для стационарных, но и для нестационарных процессов.
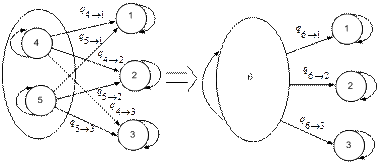
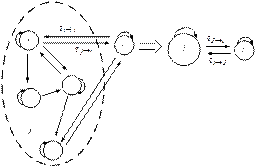
Поясним сказанное выше на примере объединения двух состояний системы в одно (рис. 5.4).
Процесс останется Марковским, то есть интенсивности переходов q 6®1, q 6®2, и q 6®3 останутся независимыми от времени при выполнении следующих условий: q 4®1 = q 5®1, q 4®2 = q 5®2, и q 4®3 = = q 5®3. При этом неважно, равны или нет интенсивности q 4®1, q 4®2 и q 4®3.
Выведем формулы для вычисления вероятностей и частоты возникновения совокупных состояний. Рассмотрим схему (рис. 5.5), в которой несколько состояний j объединены в одно совокупное состояние J.
Вероятность состояния J, обозначаемая PJ, равна сумме всех вероятностей Pj:
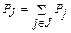 . .
| (5.12) |
Вероятности Pj можно складывать, так как события, заключающиеся в том, что система находится в одном из состояний j, взаимоисключающие. Частота возникновения состояний J, обозначаемая W J, равна сумме всех частот перехода из состояния j в состояние i, находящееся вне J:
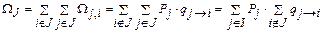 , ,
| (5.13) |
где при втором преобразовании была выполнена подстановка по формуле (5.8).
Чтобы найти решение, используя пространство состояний, получившееся после объединения состояний j, необходимо знать обозначенные на рис. 5.5 интенсивности переходов qi®J и qJ®i. Их можно вычислить, исходя из того, что частота переходов от i к J должна быть такой же, как частота переходов от i ко всем состояниям j до их объединения, и аналогично для переходов от J к i. Согласно (5.8) эти требования можно представить как
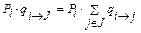 ; ; 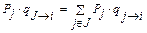 , ,
| (5.14) |
откуда

| (5.15) |
и
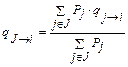 . .
| (5.16) |
Если удовлетворены условия объединяемости, то есть если qj®i одинаковы для всех j, то уравнение (5.16) упрощается:
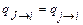 для для 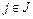 . .
| (5.17) | |
| ||
| Рис. 5.4. Объединение состояний 4 и 5 в состояние 6 при условии, что процесс должен остаться Марковским |
|
| Рис. 5.5. Объединение состояний j в совокупное состояние J |
В заключение найдем интенсивность переходов между двумя совокупными состояниями I и J, каждое из которых состоит из нескольких исходных состояний (естественно непересекающихся). Схематически такая система изображена на рис. 5.6; согласно уравнениям (5.15) и (5.16) эти интенсивности равны:
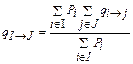 , , 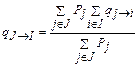 . .
| (5.18) |
Если удовлетворены условия объединяемости, то эти уравнения приводятся к виду
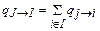 для для 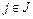 ; ;  для для 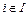 , ,
| (5.19) |
поскольку внутри I все qi®j не зависят от i, а внутри J все qj®i не зависят от j.

|
| Рис. 5.6. Переходы между двумя совокупными состояниями |
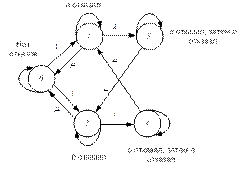
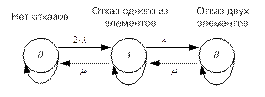
Пример 1. Рассмотрим пространство состояний дублированной системы с неявным резервированием при ограниченном аварийном ремонте (возможен только их последовательный ремонт). Предположим, что оба элемента имеют одинаковую интенсивность отказов l и восстановления m. Пространство состояний тогда приобретает вид, показанный на рис. 5.7, а. После объединения двух состояний, характеризуемых отказом одного элемента в состоянии А, и двух состояний, характеризуемых отказом двух элементов в состоянии В, получается диаграмма пространства состояний, изображенная на рис. 5.7, б.
Легко убедиться в том, что при этом объединении состояний условия объединяемости удовлетворяются.
Для состояния А:
 и
и 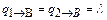 – условие объединяемости выполняется.
– условие объединяемости выполняется.
Для состояния B:
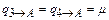 – условие объединяемости выполняется.
– условие объединяемости выполняется.
Вычислим интенсивности переходов в новой диаграмме. Согласно уравнению (5.15)
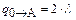 . .
|
Согласно (5.16) или (5.17)
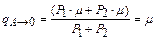 . .
|
И наконец, согласно (5.18) или (5.19)
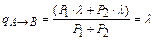 и и 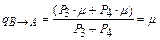 . .
|
|
| а) |
|
| б) |
Рис. 5.7. Объединение состояний (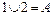 , , 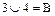 ) дублированной системы с неявным резервированием при условии возможности лишь последовательного их ремонта: a – исходная диаграмма пространства состояний; б – конечная диаграмма пространства состояний ) дублированной системы с неявным резервированием при условии возможности лишь последовательного их ремонта: a – исходная диаграмма пространства состояний; б – конечная диаграмма пространства состояний
|
Модель, изображенная на рис. 5.7, б, очевидно, значительно проще использовать для расчета, чем модель 5.7, а. Однако некоторая информация, имеющаяся в исходной диаграмме, маскируется в упрощенной диаграмме, например тот факт, что одни ремонты элементов могут выполняться лишь последовательно, становится неразличимым.
Иногда может оказаться целесообразным объединить состояния, если даже условия объединяемости и не выполняются. В этих случаях уравнения, получаемые из диаграммы после объединения состояний, не могут быть использованы для определения неустановившихся значений вероятностей состояний. Несмотря на это, асимптотические значения вероятности состояний и частоты возникновения состояний вычисляются верно.
Пример 2. Рассмотрим пространство состояний, изображенное на рис. 5.7, а. Если объединить состояния 3 и 4, но не объединять состояния 1 и 2, то получится схема, изображенная на рис. 5.8.
|
| Рис. 5.8. Объединение состояний, отвечающий отказу двух элементов (рис. 5.7, а) |
При таком объединении условия объединяемости не выполняются:
 и
и 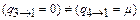 .
.
Но, несмотря на это, асимптотические значения вероятности состояний вычисляются верно. Интенсивности переходов для диаграммы, изображенной на рис. 5.9, находятся следующим образом.
Согласно выражению (5.15)
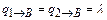 . .
|
Согласно (5.16)
 . .
|
Причем вероятности сокращаются из соображений симметрии, так как P 3 =P 4. Аналогично
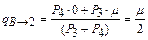 . .
|
Пример 3. Временная диаграмма состояний системы, которая может находиться в пяти состояниях, представлена на рис. 5.9.

|
| Рис. 5.9. Временная диаграмма состояний системы |
Известно следующее:
- продолжительность пребывания системы в каждом из состояний подчинена экспоненциальному закону;
- средняя продолжительность пребывания системы в каждом из состояний:
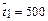 ч;
ч; 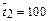 ч;
ч;  ч;
ч;  ч;
ч; 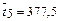 ч;
ч;
- 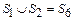 – рабочее состояние;
– рабочее состояние;  – состояние аварийного ремонта;
– состояние аварийного ремонта;  – состояние планово-предупредительного ремонта.
– состояние планово-предупредительного ремонта.
Задание:
1. Составить диаграмму пространства состояний по данной временной диаграмме состояний системы.
Определить:
- частоту появления каждого из состояний (W1, W2, W3, W4, W5);
- вероятность нахождения системы в каждом из пяти состояний в стационарном режиме работы (P 1(¥), P 2(¥), P 3(¥), P 4(¥), P 5(¥));
- интенсивности переходов из состояния в состояние (q 1®2, q 1®3, q 3®2, q 4®5 и т. д. – год-1).
2. Составить диаграмму пространства состояний для данной системы, которая имеет три состояния: S 5, S 6, S 7. Определить с помощью этой диаграммы вероятности нахождения системы в работоспособном состоянии, состоянии аварийного ремонта и в состоянии планово-предупредительного ремонта для установившегося (стационарного) процесса.
Решение:
Составим диаграмму пространства состояний по данной временной диаграмме состояний системы (рис 5.10).
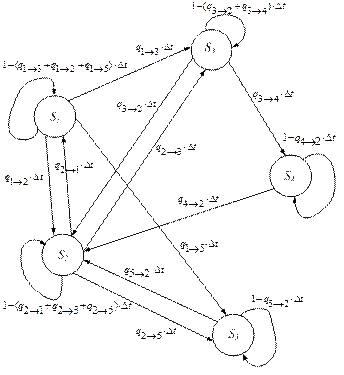
|
| Рис.. 5.10. Диаграмма пространства состояний системы |
Определим частоту появления каждого из состояний.
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
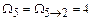 .
.
Определим вероятности нахождения системы в каждом из пяти состояний в стационарном режиме работы.
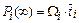 .
.
 ;
;
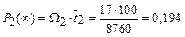 ;
;
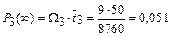 ;
;
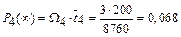 ;
;
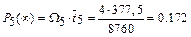 .
.
Определим интенсивности переходов из состояния в состояние.
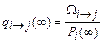 .
.
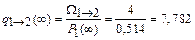 ;
;
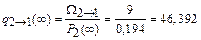 ;
;
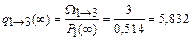 ;
;
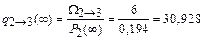 ;
;
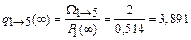 ;
;
 ;
;
 ;
;
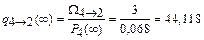 ;
;
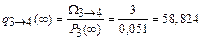 ;
;
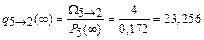 .
.
Проведем проверку правильности определения значений интенсивностей перехода системы из i- го состояния.
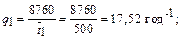
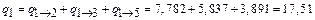 год-1.
год-1.
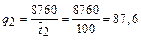 год-1;
год-1;
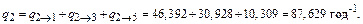
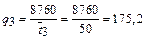 год-1;
год-1;
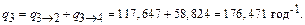
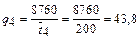 год-1;
год-1;
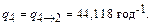
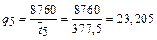 год-1;
год-1;

Составим диаграмму пространства состояний для данной системы, которая имеет три состояния: S 5, S 6, S 7 (рис 5.11).

|
| Рис. 5.11. Диаграмма пространства состояний системы |
Определим интенсивности переходов из состояния в состояние.
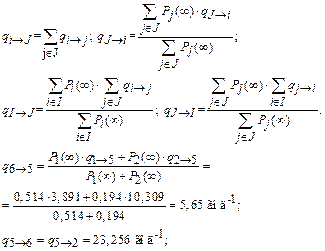
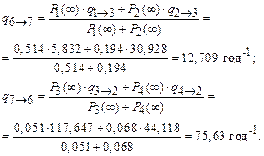
Определим вероятности нахождения системы в каждом из трех состояний в стационарном режиме работы.
Система уравнений Чемпена – Колмогорова:
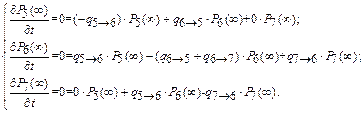
Условие нормировки:
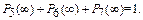
Тогда
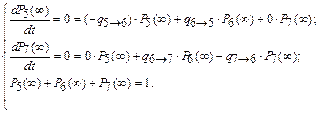
Подставив в полученную систему уравнений значения интенсивностей переходов из состояния в состояние, определим вероятности нахождения системы в состояниях S 5, S 6 и S 7.
Вероятность нахождения системы в работоспособном состоянии для стационарном режиме работы равна P 6(¥) = 0,709, в состоянии аварийного ремонта – P 7(¥) = 0,119 и в состоянии планово-предупредительного ремонта – P 5(¥) = 0,172.
Ответ:
1. W1 = 9 год-1; W2 = 17 год-1; W3 = 9 год-1; W4 = 3 год-1; W5 = 4 год-1;
P1(¥) = 0,514; P2(¥) = 0,194; P3(¥) = 0,051; P4(¥) = 0,068; P5(¥) = = 0,172;
q 1®2 = 7,782 год-1; q 2®1 = 46,392 год-1; q 1®3 = 5,832 год-1; q 2®3 = = 30,928 год-1; q 1®5 = 3,891 год-1; q 2®5 = 10,309 год-1; q 3®2 = 117,647 год-1; q 4®2 = 44,118 год-1; q 3®4 = 58,824 год-1; q 5®2 = 23,256 год-1.
2. P 6(¥)=0,709; P 7(¥)=0,119; P 5(¥)=0,172.
Пример 4. Диаграмма пространства состояний системы представлена на рис. 5.12.

|
| Рис. 5.12. Диаграмма пространства состояний системы |
Известно следующее:
- продолжительность пребывания системы в каждом из состояний подчинена экспоненциальному закону;
- все интенсивности переходов из состояния в состояние имеют одинаковые значения:
q 1®2 = q 1®3 = q 1®4 = q 1®5 = q 2®1 = q 2®3 = q 2®4 = q 2®5 = q 3®1 = q 3®2 = q 3®4 = q 3®5 = q 4®1 = q 4®2 = q 4®3 = q 4®5 = q 5®1 = q 5®2 = q 5®3 = q 5®4 = = 2 год-1;
- S 1È S 2È S 5= S 6 – работоспособное состояние; S 3È S 4= S 7 – неработоспособное состояние;
- в начальный момент времени система находится в состоянии S 1.
Задание:
Преобразовав исходную диаграмму пространства состояний в диаграмму с двумя состояниями, определить:
1) вероятность нахождения системы в работоспособном состоянии в момент времени t = 0,1 года;
2) вероятность безотказной работы в момент времени t = 0,5 года.
Решение:
1. Определение вероятности нахождения системы в работоспособном состоянии в момент времени t = 0,1года.
Преобразуем исходную диаграмму пространства состояний в диаграмму с двумя состояниями (рис. 5.13).
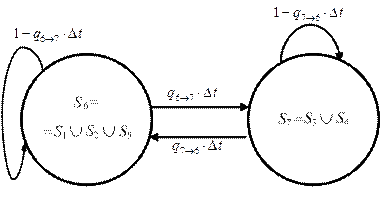
|
| Рис. 5.13. Диаграмма пространства состояний для определения вероятности нахождения системы в работоспособном состоянии в момент времени t = 0,1 года |
На рис. 5.13 S 6 – работоспособное, а S 7 – неработоспособное состояния системы.
Определим интенсивности переходов из состояния в состояние.
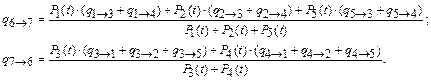
Так как условие объединяемости выполняется, то
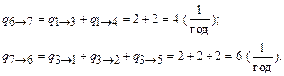
Составим систему дифференциальных уравнений Чемпена – Колмогорова с учетом условия нормировки и определим P 6 РС (t = 0,1).
Уравнения Чемпена – Колмогорова:
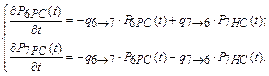
Условие нормировки: 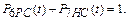
Тогда
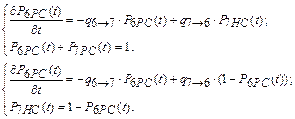
Из первого уравнения найдем P 6(t) методом разделения переменных:


В этом случае уравнение имеет два решения:
- первое общее решение:
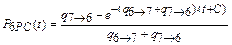 ;
;
- второе общее решение:
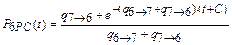 .
.
Найдем частные решения, используя начальное условие P 1(t = 0) = P6РС (t = 0) = 1. Первого частного решения не существует. Второе частное решение находится следующим образом:
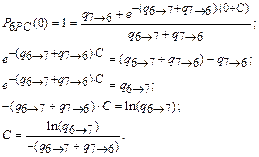
Тогда
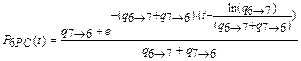 ;
;
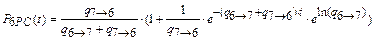 ;
;
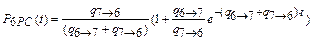 – частное решение.
– частное решение.
Вероятность нахождения системы в работоспособном состоянии в момент времени t = 0,1 года равна
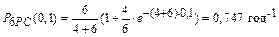 .
.
2. Определение вероятности безотказной работы в момент времени t = 0,5 года.
Составим диаграмму пространства состояний для определения вероятности безотказной работы в момент времени t = 0,5 года.
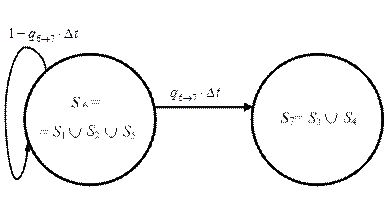
При определении вероятности безотказной работы системы принимают, что восстановление работоспособности системы из неработоспособного состояния невозможно. Диаграмма пространства состояний в этом случае выглядит следующим образом (рис. 5.14):
|
| Рис. 5.14. Диаграмма пространства состояний для определения вероятности безотказной работы системы в момент времени t = 0,5 года |
На рис. 5.14 S 6 – работоспособное, а S 7 – неработоспособное состояния системы, q 6®7 = 4год-1.
Составим систему дифференциальных уравнений Чемпена – Колмогорова с учетом условия нормировки и определим P7БР (t = 0,5 лет).
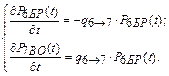
Так как при одной неизвестной имеем одно уравнение, то условие нормировки можно не использовать.
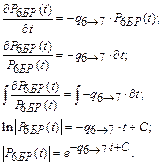
В этом случае уравнение имеет два решения:
- первое общее решение:
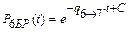 ;
;
- второе общее решение:
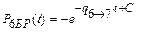 (уравнение решений не имеет, так как вероятность должна быть положительной).
(уравнение решений не имеет, так как вероятность должна быть положительной).
Найдем частное решение, используя начальные условия P 1(t = 0) = P6БР (t = 0) = 1:
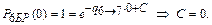
Тогда 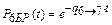 – частное решение.
– частное решение.
Вероятность безотказной работы в момент времени t = 0,5 лет:
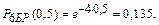
Ответ:
1. 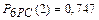 ;
;
2. 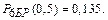
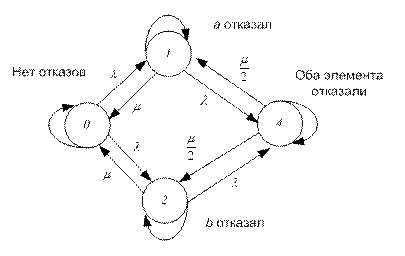
Пример 5. Два одинаковых объекта (А, В) образуют дублированную систему с резервированием замещением и ограниченным аварийным ремонтом. Планово-предупредительные ремонты на объектах не проводятся.
Известно следующее:
- объекты имеют независящие от времени интенсивности переходов: интенсивности отказов: λА = λВ = λ = 2 год-1; интенсивности восстановления из аварийного ремонта: μ АР, А = μ АР, В = µ АР = 10 год-1;
- в начальный момент времени система находится в состоянии S 1.
Задание:
1) Определить для стационарного режима работы: вероятность работоспособного состояния (РС), вероятность неработоспособного состояния (НС) и вероятность промежуточного состояния (ПС) системы, в котором один из элементов находится в работоспособном, а другой – в неработоспособном состоянии.
2) Составить диаграмму пространства состояний и систему уравнений Чемпена – Колмогорова с условием нормировки для определения вероятности безотказной работы системы.
Решение:
Составим диаграмму пространства состояний для определения вероятностей нахождения системы в работоспособном P РС(¥), неработоспособном P НС(¥) и промежуточном P ПС(¥) состояниях (рис. 5.15).

|
| Рис. 5.15. Диаграмма пространства состояний для определения вероятности нахождения системы в работоспособном состоянии (дублированная система с резервированием замещением и ограниченным аварийным ремонтом) |
Здесь приняты следующие обозначения: а, b – рабочие состояния объектов А или В; 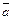 ,
, 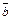 – неработоспособные состояния А или В (в этом состоянии на объекте проводится аварийный ремонт либо объект ожидает его начала); a, b − режим ожидания объекта А или В.
– неработоспособные состояния А или В (в этом состоянии на объекте проводится аварийный ремонт либо объект ожидает его начала); a, b − режим ожидания объекта А или В.
Система может находиться в шести состояниях: S 1 = a Ç b – состояние, в котором А находится в рабочем состоянии, а B – в режиме ожидания; S 2 = a Ç b – состояние, в котором B находится в рабочем состоянии, а A – в режиме ожидания;  – состояние, в котором А находится в неработоспособном состоянии (состоянии аварийного ремонта), а B – в рабочем состоянии;
– состояние, в котором А находится в неработоспособном состоянии (состоянии аварийного ремонта), а B – в рабочем состоянии; 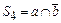 – состояние, в котором B находится в неработоспособном состоянии (состоянии аварийного ремонта), а A – в рабочем состоянии;
– состояние, в котором B находится в неработоспособном состоянии (состоянии аварийного ремонта), а A – в рабочем состоянии; 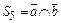 – состояние, в котором система находится в неработоспособном состоянии. При этом на объекте A производится аварийный ремонт, так как он раньше отказал. Объект B подвергнется аварийному ремонту после окончания работ на объекте А;
– состояние, в котором система находится в неработоспособном состоянии. При этом на объекте A производится аварийный ремонт, так как он раньше отказал. Объект B подвергнется аварийному ремонту после окончания работ на объекте А; 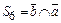 – состояние, в котором система находится в неработоспособном состоянии. При этом на объекте B производится аварийный ремонт, так как он раньше отказал. Объект A подвергнется аварийному ремонту после окончания работ на объекте B.
– состояние, в котором система находится в неработоспособном состоянии. При этом на объекте B производится аварийный ремонт, так как он раньше отказал. Объект A подвергнется аварийному ремонту после окончания работ на объекте B.
При этом
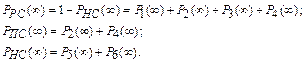
Составим систему дифференциальных уравнений Чемпена – Колмогорова с учетом условия нормировки для стационарного режима и определим вероятности нахождения системы в работоспособном РРС (∞), неработоспособном РНС (∞) и промежуточном РПС (∞) состояниях.
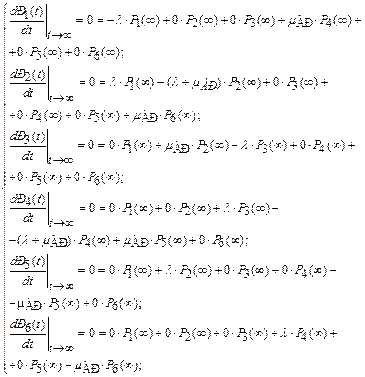
Условие нормировки:
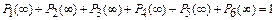 .
.
Так как диаграмма пространства состояний симметрична относительно линии ОО´, то

Тогда
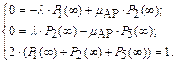
Решая данную систему уравнений, получим:
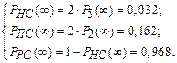
Составим диаграмму пространства состояний для определения вероятности безотказной работы.
При составлении диаграммы пространства состояний в этом случае принимают, что восстановление работоспособности системы из неработоспособного состояния невозможно (рис. 5.16).
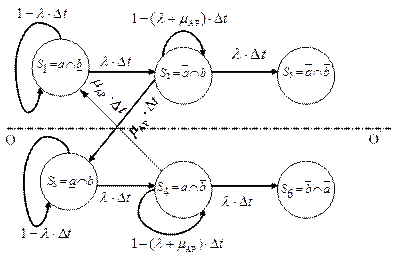
|
| Рис. 5.16. Диаграмма пространства состояний для определения вероятности безотказной работы системы (дублированная система с резервированием замещением и ограниченным аварийным ремонтом) |
При этом
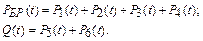
Составим систему дифференциальных уравнений Чемпена – Колмогорова с учетом условия нормировки.
Система уравнений Чемпена – Колмогорова

Условие нормировки:
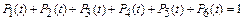
Ответ:
 ;
; 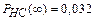 ;
;  .
.
Пример 6. Два одинаковых объекта А и В образуют дублированную систему с постоянным резервированием и ограниченным аварийным ремонтом. Планово-предупредительные ремонты на объектах не производятся.
Известно следующее:
- объекты имеют независящие от времени интенсивности переходов: интенсивности отказов: λА = λВ = λ = 2 год-1; интенсивности восстановления из аварийного ремонта: μ АР, А = μ АР, В = µ АР = 10 год-1;
- в начальный момент времени система находится в состоянии S 1.
Задание:
1) Определить для стационарного режима работы: вероятность работоспособного состояния (РС), вероятность неработоспособного состояния (НС) и вероятность промежуточного состояния (ПС) системы, в котором один из элементов находится в работоспособном, а другой – в неработоспособном состоянии.
2) Составить диаграмму пространства состояний и систему уравнений Чемпена – Колмогорова с условием нормировки для определения вероятности безотказной работы системы.
Решение:
Составим диаграмму пространства состояний для определения вероятностей нахождения системы в работоспособном PРС (¥), неработоспособном PНС (¥) и промежуточном PПС (¥) состояниях (рис. 5.17).

|
| Рис. 5.17. Диаграмма пространства состояний для определения вероятности нахождения системы в работоспособном состоянии (дублированная система с постоянным резервированием и ограниченным аварийным ремонтом) |
Система может находиться в пяти состояниях: S 1 = a Ç b – состояние, в котором А и B находятся в рабочем состоянии; состояния S 2 – S 5 аналогичны состояниям, описанным в примере 5.
При этом
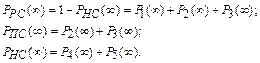
Составим систему дифференциальных уравнений Чемпена – Колмогорова с учетом условия нормировки для стационарного режима и определим вероятности нахождения системы в работоспособном Р РС(∞), неработоспособном Р НС(∞) и промежуточном Р ПС(∞) состояниях.
Система уравнений Чемпена – Колмогорова:
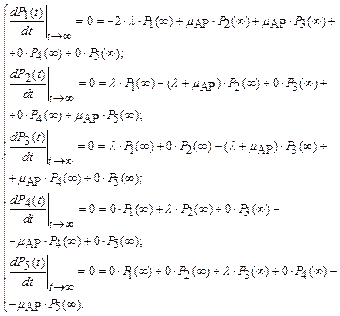
Условие нормировки:

Так как диаграмма пространства состояний симметрична относительно линии ОО´, то
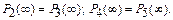
Тогда
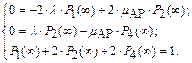
Решая данную систему уравнений, получим:
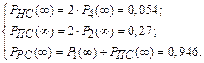
Составим диаграмму пространства состояний для определения вероятности безотказной работы.
При определении вероятности безотказной работы системы принимают, что восстановление работоспособности системы из неработоспособного состояния невозможно (рис. 5.18).

|
| Рис. 5.18. Диаграмма пространства состояний для определения вероятности безотказной работы системы (дублированная система с постоянным резервированием и ограниченным аварийным ремонтом) |
Составим систему дифференциальных уравнений Чемпена – Колмогорова с учетом условия нормировки.
Уравнения Чемпена – Колмогорова:
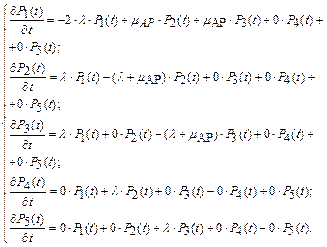
Условие нормировки: 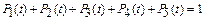 .
.
Ответ:
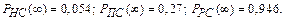
Примечание. При одинаковых интенсивностях переходов из состояния в состояние элементов надежность дублированной системы с резервированием замещением выше, чем системы с постоянным резервированием.
Date: 2015-07-25; view: 728; Нарушение авторских прав