Линейное преобразование, сопряженное данному

1º. Определения, свойства.

Здесь изучаются линейные преобразования в евклидовых пространствах, т.е. в линейных пространствах со скалярным произведением.

Определение 1. Линейное преобразование евклидово пространство называется сопряженным данному преобразованию 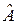, если 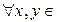E :

(1)

Лемма 1. а) Если произведение данной строки на произвольный столбец равно нулю, то строка равна нулю;

б) Если произведение произвольной строки на данный столбец равно нулю, то столбец состоит из нулей.

Доказательство:

а) Рассмотрим строку 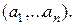Ее произведением на столбец 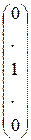– –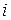ая строка равно 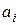и равно 0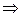

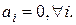
б) Аналогично. ■

Пусть E 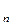– –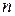мерное евклидово пространство и пусть для симметричного преобразования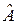 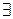сопряженное ему преобразование .

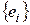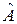Пусть – базис в E . Выясним, как связаны матрицы и 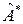. Пусть в базисе 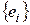они имеют матрицы 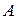и 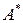. Тогда (1) примет вид:

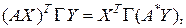
где 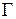– матрица Грама базиса 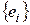. Тогда

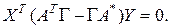
в силу леммы 1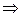

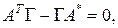(2)

где 0 – нулевая матрица.

Если базис 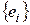– ортонормированный, то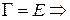

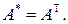(3)

Утверждение 1. Каждое линейное преобразование в евклидовом пространстве имеет сопряженное преобразование, причем единственное.

Доказательство:

В E 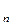выберем ортонормированный базис 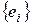. Пусть 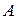– матрица линейного преобразования 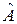и пусть 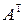– матрица некоторого преобразования 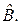Тогда условие (1) с преобразованием 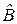приводит к следующему:

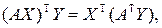
т.е. 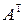– матрица сопряженного преобразования. Если бы было два преобразования, сопряженных 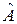, то в силу (3) их бы матрицы совпадали. ■

Date: 2015-07-25; view: 579; Нарушение авторских прав