Практическая работа

МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ

ПРИРОДЫ, ОБЩЕСТВА И ЧЕЛОВЕКА «ДУБНА»

КАФЕДРА ОБЩЕЙ ФИЗИКИ

РАСЧЕТ

ОРБИТЫ ДВИЖЕНИЯ ПЛАНЕТЫ

МЕТОДОМ ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ

Практическая работа

Разработал: проф., д.т.н. Гребенкин М.Ф.

Дмитров 2002

1. Цель работы:

Цель данной работы заключается в том, чтобы студент на основе решения конкретной практической задачи (расчет орбиты движения планеты вокруг Солнца) более глубоко понял суть кинематических и динамических уравнений механики, познакомился с основной задачей механики и практически овладел методом численного интегрирования уравнений механики, как универсального метода решения такого типа задач.

Литература: Р. Фейнман, Р. Лейтон, М. Сэндс. «Фейнмановкие лекции по физике», том 1, глава 9, п. 4, 5, 6. Издательство «Мир», Москва, 1967 г.

Дополнительно: «Физика. Механика. 9 класс». Учебник под редакцией Г. Я. Мякишева. Москва. Издательство «Дрофа», 1997 г. п.2.9, 2.10.

1. Основная задача механики.

В случае классической механики с помощью законов Ньютона можно не только объяснить наблюдаемые механические явления, но и предсказывать их течение.

Основная (прямая) задача механики состоит в нахождении положения и скорости тела в любой момент времени, если известны его положение и скорость в начальный момент времени и действующие на него силы.

Эта задача решается с помощью второго закона Ньютона – основного закона классической механики:

, (1)

где – масса тела, – ускорение тела, , , 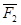и т.д. – действующие на тело силы ().

Введя декартову систему координат уравнение (1) можно переписать в виде:

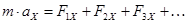
(2)

,

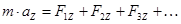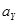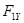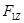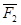где , , , , , , , , – соответственно проекции вектора ускорения и векторов сил , и т.д. на координатные оси X, Y, Z.

Уравнения (1) и (2) называются динамическими уравнениями. Кроме них при решении основной задачи механики используются кинематические уравнения, связывающие координаты, скорость и ускорение тела:

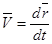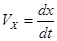; ; ; (4)

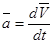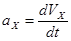; ; ; , (5)

где – скорость тела.

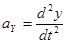; ; ; , (6)

Таким образом, если известны действующие на тело силы ; и т.д., т.е. силы известны в каждой точке пространства и в каждый момент времени, то решение основной задачи механически сводится к решению дифференциального уравнения:

(7)

или системой уравнений:

(8)

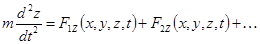
Как известно уравнения (7) или (8) имеют много решений, поэтому для однозначного определения положения и скорости тела в данный момент времени необходимо знать положение и скорость тела в начальный момент времени, т.е. другими словами, надо знать (или задать) начальные условия:

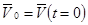, (9)

или

;

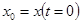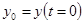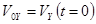; (10)

; ,

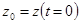полагая, что в начальный момент времени .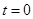

Если с точки зрения математики решение основной задачи механики сводится к решению дифференциального уравнения (7) при условии (9) (или уравнении (8) при условиях (10)), то с точки зрения физики главная проблема заключается в определении действующих на тело сил, причем необходимо знать зависимость сил от координат и времени. Такую зависимость в принципе можно получить экспериментальным путем, но в ряде важных случаев она выражается аналитически (с помощью формул), например:

a) Сила упругости (закон Гука): , где – коэффициент (жесткость пружины);

b) Сила всемирного тяготения:

;

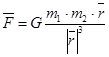что позволяет теоретически рассчитывать траекторию движения тела и его скорость для любых конкретно интересующих нас случаев.

1. Метод численного интегрирования. [1]

Пусть в данный момент времени 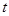тело находится в точке 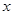и движется со скоростью 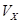. Каковы будут его положение и скорость спустя небольшой промежуток времени 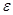, т.е. в момент времени ? Если мы сможем ответить на этот вопрос, то проблема будет решена, так как, исходя из начальных условий, т.е. из положения и скорости в некоторый начальный (нулевой) момент времени, можно сказать, каковы они будут в первый момент, а, затем, зная положение и скорость в первый момент времени, можно найти их в следующий момент времени и т.д. Таким образом, шаг за шагом выстраивается вся картина движения.

Для любого момента времени 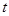при очень малом 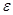можно с достаточно хорошей точностью найти положение в момент через скорость и положение в момент .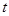

, (11)

где 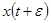– новая координата тела, 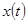– старая координата тела, 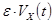– приращение (изменение координаты).

С точки зрения физики выражение (11) основано на том, что всегда можно выбрать такой малый интервал времени 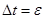, во время которого скорость тела, вообще говоря, меняющаяся со временем, практически не меняется, а тогда изменение координаты можно вычислить по простой формуле: .

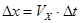C точки зрения математики выражение (11) прямо следует из определения понятия производной:

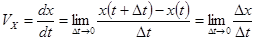
Итак, при известных значениях скорость 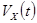положение тела (координата 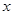) определяется вычислениями, основанными на выражении (11). Ну, а что теперь можно сказать о скорости? Чтобы определить скорость в момент времени , очевидно, нужно знать, как она изменяется со временем, т.е. нужно знать ускорение. Формально эта задача решается точно так же, как и для координаты :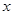

(12)

Опять таки, выражение (12) основано на том, что всегда можно выбрать такой маленький интервал времени 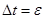, что, вообще говоря, меняющееся со временем ускорение в пределах выбранного интервала времени 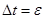практически не меняется, и тогда изменение скорости можно вычислить по простой формуле:

Итак, при известных значениях ускорения 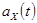скорость тела 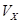определяется вычислениями, основанными на выражении (12). Уравнения (11) и (12) – кинематические, они просто говорят, что из-за наличия скорости меняется координата. Ну, а что можно сказать об ускорении 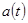? Информацию об ускорении дает нам второй закон Ньютона (2):

(13)

Уравнение (13) уже динамическое, потому что оно связывает ускорение с силой. И если силы нам известны, то, последовательно используя уравнения (13), (12) и (11), можно рассчитать координату и скорость тела в любой наперед заданный момент времени.

Следует отметить три обстоятельства.

Во-первых, ясно, что вычисления с использованием уравнений (11) – (13) приближенные, но их можно сделать сколь угодно точными, просто уменьшая величину 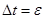( 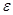называют шагом интегрирования). Ошибка вычислений ~ ε ².

Во-вторых, чтобы вычислить координату и скорость тела в момент времени, значительно отстоящий от начального, при малых значениях 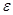требуется проделать очень много расчетов, хотя сами расчеты простые. Эта трудность в настоящее время легко преодолевается с помощью ЭВМ.[2]

В-третьих, уравнения (11) – (13) относятся к 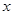, 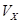и , т.е. к проекциям радиус-вектора, вектора скорости и вектора ускорения на ось X (одномерный случай). Ясно, что такие же уравнения можно написать и для 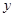, , 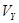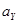и 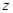, , , т.е. рассмотреть двумерный случай и самый общий трехмерный случай движения тела; лишь бы были известны значения сил, действующих на тело.

В заключение этого раздела несколько модифицируем наш метод, что позволит при том же шаге интегрирования увеличить точность. Заметим, что новое положение тела равно старому плюс интервал времени 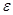, умноженный на скорость. Но что это за скорость? В какой момент времени? В начале интервала скорость одна, а в конце интервала, хотя и мало изменившаяся, но, вообще говоря, другая. Прием состоит в том, чтобы брать скорость в середине интервала 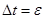. Если известна скорость в настоящий момент и известно, что она, хотя и мало, но меняется, как же можно надеяться получить удовлетворительный результат, считая, что тело все время движется с той же скоростью, что и в настоящий момент? Более разумно использовать какую-то среднюю скорость между началом и концом интервала. Те же рассуждения применимы к изменению самой скорости: для подсчета ее изменений нужно использовать ускорения в средней точке между двумя моментами времени, в которых необходимо найти скорость. Таким образом, реально мы будем пользоваться следующими уравнениями: положение в конце интервала равно положению в начале плюс интервал 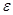, умноженный на скорость в середине интервала. Эта скорость, в свою очередь равна скорости в середине предыдущего интервала (т.е. в момент времени t-ε) плюс ускорение в начале интервала умноженное на :

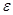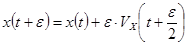
(14)

В начале вычисления мы знаем 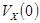, а не . Чтобы получить , воспользуемся дополнительным уравнением

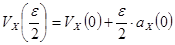. (15)

Теперь все готово к расчетам, с использований уравнений (14) и (15).

1. Постановка задачи по расчету орбиты движения планеты.

В качестве примера решения основной задачи механики с помощью метода численного интегрирования рассмотрим расчет движения орбиты планеты[3] вокруг Солнца. Предположим, что Солнце бесконечно тяжелое в том смысле, что его движение не будет приниматься в расчет. Допустим, что планета начинает свое движение в известное точке и имеет в этой точке определенную скорость (начальные условия). Планета движется вблизи Солнца по какой-то кривой, и мы попытаемся определить с помощью уравнений движения Ньютона и его же закона всемирного тяготения, что это за кривая. В некоторый (начальный) момент времени планета находится в каком-то определенном месте; на расстоянии от Солнца; в этом случае на нее действует сила , направленная по прямой к Солнцу: (см. рис.1). Чтобы рассуждать дальше, надо выяснить какое ускорение вызывает эта сила. Выберем координатную систему X, Y, Z таким образом, чтобы Z-координата как скорости, так и силы равнялась нулю. Тогда не будет никаких причин у планеты в своем движении выйти за плоскость XY, и задача станет двумерной. Из рис.1 видно, что горизонтальная компонента силы 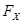() так относится к полной ее величине 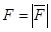, как координата 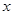относится к расстоянию (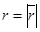). Это следует из подобия треугольников. Кроме того, если 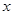положительна, то 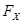отрицательна, и наоборот.

Таким образом или 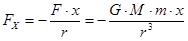и соответственно .

С использованием второго закона Ньютона имеем:

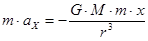
(16)

Именно эту систему уравнений мы и должны решить. Видно, что уравнения (16) связывают значения ускорений и 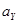с координатами планеты x,y в любой момент времени: 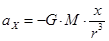; 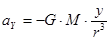, т.е. есть все предпосылки для использования метода численного интегрирования (уравнение 14).

Упростим себе задачу тем, что положим 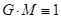( – гравитационная постоянная, – масса Солнца). Это всегда можно сделать соответствующим выбором системы единиц измерения физических величин. Тогда значения 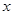, , 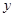, , 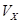, 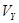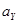и 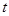будут исчесляться в неких условных единицах, что, однако, не повлияет на физическую сущность рассматриваемой задачи.

Итак:

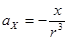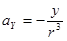; ; (17)

1. Конкретный пример решения.

Пусть заданы начальные условия в виде:

; ; ;

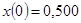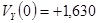; ; (18)

Отсюда находим:

; ;

; ;

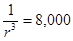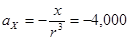Возьмем интервал времени (шаг интегрирования) .

Вычислим компоненты и 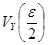по уравнению (15):

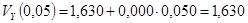
А теперь начнем основной расчет по уравнению (14):

;

;

;

;

;

;

;

;

;

;

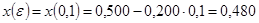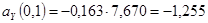и т.д.

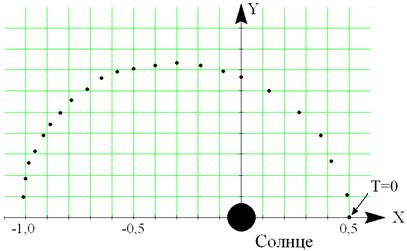
Рис. 2. График движения планеты вокруг Солнца

В результате мы будем получать координаты планеты с течением времени, и приблизительно за 20 шагов интегрирования будет прослежена половина пути нашей планеты вокруг Солнца (см. рис. 2). Точки представляют собой последовательное положение планеты через каждую десятую долю выбранной нами единицы времени. Видно, что планета сначала двигалась быстро, а затем – все медленней и медленней. Видна также и форма кривой движения планеты. Итак, мы теперь реально знаем, как можно вычислить движение планеты, на которую действует сила всемирного тяготения!

1. Заключение

При выполнении данной практической работы студенту, прежде всего, надо получить у преподавателя задание в виде начальных условий для расчета, например, в виде (18). Расчет следует производить в условной системе единиц по уравнениям (14), (15) и (17). Результаты расчетов должны быть представлены в виде таблицы следующего вида (пример):

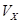
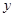
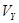
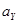
	0,500		-4,000	0,000		0,000	0,500	8,000
0,05		-0,200			1,630
0,10	0,480		-3,680	0,163		-1,256	0,507	7,675
0,15		-0,568			1,505
0,20	0,423		-2,910	0,313		-2,150	0,526	6,873
0,25		-0,859			1,290
0,30	0,337		-1,960	0,442		-2,570	0,556	5,824

Расчет следует вести аккуратно, следить за знаками величин. Рекомендуется результаты расчетов (координаты планеты) сразу же (в предварительном плане) откладывать на графике (см. рис. 2) (желательно на «миллиметровке») с тем, чтобы в случае ошибки в расчетах сразу же заметить это по искажению формы траектории планеты и своевременно исправить ошибку. Рекомендуется также творчески относиться к величине шага интегрирования 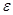; шаг можно увеличить, если траектория мало меняется со временем; и наоборот, шаг следует уменьшить, если требуется выявить быстро меняющиеся детали траектории. Могут быть заданы такие начальные условия, что траектория будет получаться незамкнутой. Не следует в этом случае считать «до бесконечности», можно ограничиться разумным числом шагов; при этом следует просчитать часть траектории при обратном течении времени (шаг 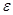брать со знаком «минус»), восстановив «прошлую» траекторию планеты до начального момента времени. Окончательный вариант рассчитанной орбиты следует начертить (напечатать) на отдельном листе (на «миллиметровке») с указанием автора расчетов и начальных условий.

Контрольные вопросы:

1. Как будет меняться траектория движения планеты при изменении начальных условий, в частности, начальной скорости?
2. Можно ли реально считать массу Солнца бесконечной? Что будет, если под действием силы всемирного тяготения двигаются сравнимые по массе тела?
3. Можно ли методом численного интегрирования рассчитать орбиты движения нескольких планет с учетом их взаимного влияния друг на друга?
4. Какие технические средства следует привлечь для облегчения расчетов?

Начальные условия для расчетов

№ п/п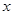
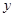
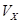
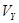
	0,500	0,000	0,000	1,630
	0,000	0,500	1,630	0,000
	0,500	0,000	0,000	-1,600
	0,000	0,500	-1,600	0,000
	0,000	0,500	1,600	0,000
	2,000	2,000	0,000	0,000
	2,000	0,000	0,000	1,000
	2,000	0,000	0,000	0,500
	2,000	0,000	0,000	0,200
	2,000	0,000	0,000	0,100
	-0,500	0,000	0,000	1,600
	1,000	0,000	0,000	-1,500
	0,800	0,000	0,000	-2,000
	0,800	0,000	0,000	-1,800
	0,800	0,000	0,000	-1,500
	0,800	0,000	0,000	1,200
	0,800	0,000	0,000	1,000
	0,800	0,000	0,000	-0,700
	0,800	0,000	0,000	-0,500
	0,800	0,000	0,000	-0,300
	-0,500	0,000	0,000	-1,500
	0,000	-0,500	-1,500	0,000
	0,000	-0,500	1,500	0,000
	-0,500	0,000	0,000	1,500
	0,000	-0,500	1,000	0,000
	0,200	0,000	0,000	2,000
	0,000	0,200	-2,000	0,000
	1,000	0,000	0,000	-1,000
	0,700	0,000	0,000	-1,600
	0,000	0,700	1,600	0,000

Примечание: в работе предполагается расчёты вести с помощью калькулятора, но, по желанию, можно воспользоваться таблицами Exel или какой-либо другой расчётной программой. Главное – ясное понимание того, что делается.

[1] Метод численного интегрирования рассмотрен кратко применительно к задачам механики. Стоит, однако, при этом помнить, что именно развитие этого метода привело к открытию дифференциального и интегрального исчисления.

[2] На современных компьютерах меньше чем за минуту можно «прогнать» Юпитер вокруг Солнца и при этом ещё с точностью до одной миллиардной учесть все возмущения от других планет.

[3] Под планетой будем здесь понимать и космическое тело, движущееся вокруг Солнца по замкнутой орбите (большие и малые планеты, астероиды, кометы), и космическое тело, движущееся по незамкнутой орбите (по гиперболе), т.е. «пришельцев» из далёкого космоса.