
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Коническая поверхность вращения
|
|
Конической поверхностью называется поверхность, образованная движением прямой АВ, перемещающейся в пространстве через неподвижную точку S и пересекающей кривую линию MN. Прямая АВ называется образующей, линия MN – направляющей, а точка S – вершиной конической поверхности (рис.4).
Рис.4
Конусом (рис.5) называется тело, ограниченное частью конической поверхности, расположенной по одну сторону от вершины, и плоскостью, пересекающей все образующие по ту же сторону от вершины.

Рис. 5 Рис. 6
Конус можно рассматривать как тело, образованное вращением прямоугольного треугольника вокруг катета, принятого за ось вращения. Сечение прямого кругового конуса плоскостью, перпендикулярной к его оси, есть круг (рис. 6).
 Проецирование прямого кругового конуса с вертикальной осью (рис. 7) аналогично проецированию пирамиды. В основании конуса будет окружность, с которой следует начинать чертёж. Если ось конуса перпендикулярна горизонтальной плоскости проекций, горизонтальная проекция будет в виде круга, а фронтальная и профильная – в виде треугольников с вершиной S.
Проецирование прямого кругового конуса с вертикальной осью (рис. 7) аналогично проецированию пирамиды. В основании конуса будет окружность, с которой следует начинать чертёж. Если ось конуса перпендикулярна горизонтальной плоскости проекций, горизонтальная проекция будет в виде круга, а фронтальная и профильная – в виде треугольников с вершиной S.
Рис. 7
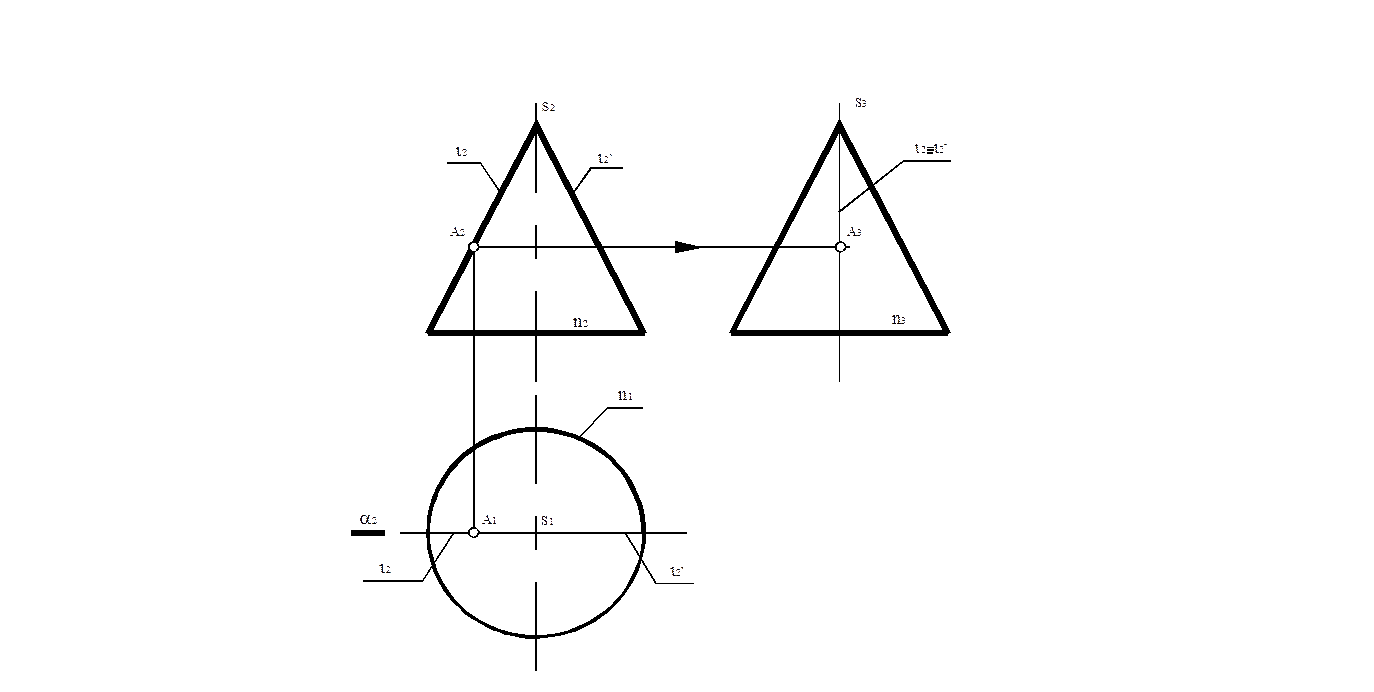
Рис.8,а
Фронтальный очерк конической поверхности (рис. 8,а) определяется проекцией главного меридиана, т.е. проекциями прямолинейных образующих ι´ и ι, расположенных в секущей плоскости α║ П2. Секущая плоскость β║П3 (рис. 8,б) рассекает конус по образующим κ и κ´, профильные проекции которых определяют профильный очерк поверхности.

Рис. 8,б
Профильные проекции ι3 и ι3´ образующих ι и ι´, а также фронтальные проекции κ2 и κ2´ образующих κ и κ´ совпадают с соответствующими проекциями оси вращения i. Горизонтальная проекция поверхности определяется проекцией n1 окружности n – линии ограничения данной поверхности. Это наибольшая из параллелей, которая на П2 и П3 проецируется в виде отрезков прямых n2 и n3, равных её диаметру.

Рис. 9,а
Линии каркаса параллелей и меридианов показаны на рис. 9,а и рис. 9,б. Параллели радиусов r и R, являющихся результатом пересечения конуса с плоскостями γ║ П1 и ω║ П1, на П1 проецируются без искажения.

Рис. 9,б
Если на поверхности конуса дана одна проекция точки, то через неё проводим образующую, соединяющую основание с вершиной, и, найдя все три проекции образующей, переносим на неё с помощью линий связи проекции данной точки. Вместо образующей можно провести вспомогательную параллель и с её помощью найти проекции точки (рис. 10, а и рис. 10, б).

Рис. 10,а

Рис. 10, б
Date: 2015-07-24; view: 1417; Нарушение авторских прав