Уравнения линии с распределенными параметрами

Напряжения и ток в линии являются функциями двух независимых переменных – пространственной координаты x, определяющей место наблюдения, и времени t, определяющей момент наблюдения. Считается, что направление координаты x совпадает с осью линии.

Необходимо найти пространственно-временное распределение величины тока в линии i (x, t) и напряжения между проводами u (x, t). В этом случае также можно определить процесс передачи энергии по линии, когда приемники и источники находятся на обоих концах линии.

Приняв положительное направление тока в линии слева направо, условимся называть "началом" левый конец линии. Расстояние от начальной точки до произвольной обозначим через x, а от конца – через x '. Вся длина линии l = x + x '.

Выделим элементарный участок D x на расстоянии x от начала. Пользуясь первичными параметрами R ₀, L ₀, C ₀, G ₀, отнесенными к единице длины линии, представим приближенно участок D x в виде схемы замещения (рис. 13.1).

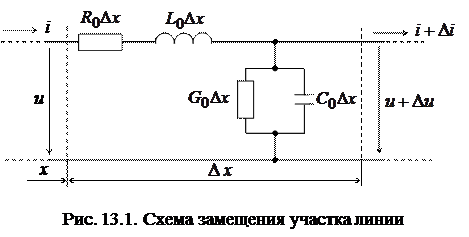Обозначим:

u – напряжение между верхним и нижним проводом в точке x;

D u – приращение напряжения на участке D x;

i – ток в точке x;

D i – приращение тока на участке D x.

Уравнения для приращений напряжения и тока на элементе D x линии запишутся:

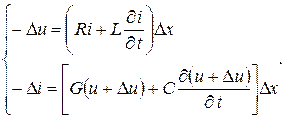(13.1)

Это уравнение в частных производных. По мере стремления D x к нулю степень точности этих уравнений повышается, причем величина второго порядка малости 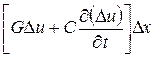в правой части второго уравнения может быть опущена.

В этом случае длинная линия рассматривается как цепная схема с бесконечно большим количеством звеньев, электрические параметры которых бесконечно малы.

Разделив обе части уравнений на D x и перейдя к пределу D x ® 0, получим дифференциальные уравнения линии

(13.2)

Эти уравнения носят название телеграфных.

Если за начало отсчета принять конец линии, т.е. ввести координату x ', уравнения примут вид:

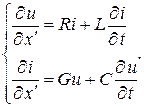(13.3)

Уравнения (13.2) и (13.3) решаются однозначно при использовании начальных и граничных условий. Начальными условиями будут служить значения напряжения и тока в начале и конце линии в момент времени, принятый за нуль. Граничные условия определяются связями между напряжением и током в начале или в конце линии и зависят от заданного режима работы линии.

Date: 2015-07-24; view: 332; Нарушение авторских прав