Сигналы с частотной модуляцией

Частотно модулированным (ЧМ) сигналом называется сигнал, приращение мгновенной частоты которого относительно среднего значения пропорционально амплитуде модулирующего первичного электрического сигнала U_W (t).

Изменение мгновенной частоты w (t) ЧМ сигнала описывается как функция времени следующим выражением

w (t) = w_H + Dw (t). (2)

Максимальное отклонение частоты

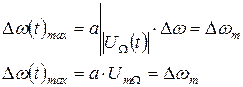, (3)

где а – коэффициент пропорциональности.

Максимальное отклонение частоты Dw (t) _max относительно среднего значения называется девиацией частоты.

Известно, что при ЧМ полная фаза модулированного колебания определяется интегралом от модулирующего сигнала U_W (t):

. (4)

С учетом (4) аналитическое выражение для ЧМ сигнала запишем следующим образом:

. (5)

Если модулирующий сигнал U_W (t) имеет частоту одного тона, то (5) примет вид:

, (6)

где - индекс ЧМ, который равен отношению девиации частоты Dw_m к частоте модулирующего колебания W:

. (7)

Временные диаграммы при ЧМ приведены на рис. 1.

Для определения спектра ЧМ сигнала воспользуемся выражением (6) и, раскрывая косинус суммы двух углов по правилу:

cos (a+b) =cosa×cosb – sina×sinb,

получим: (8)

Сравнивая это выражение с выражением для АМ при тональной модуляции, видим, что спектр ЧМ сигнала значительно сложнее, т.к. здесь соединяются сложные функции cos (m_ЧМ sin W t) и sin (m_ЧМ sin W t), которые представляются тригонометрическим рядом вида:

(9)

(10)

где J_n(m) – бесселева функция первого рода п -го порядка от аргумента, который рассмотрим по графикам позже.

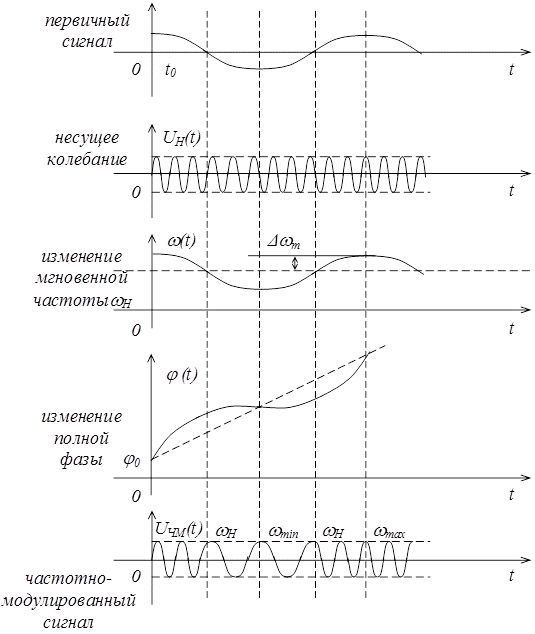
Рис. 1. Временные диаграммы при ЧМ

Подставляя в (8) ряды (9) и (10) и заменяя произведения косинусов и синусов на суммы

,

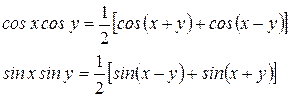приходим к окончательному выражению:

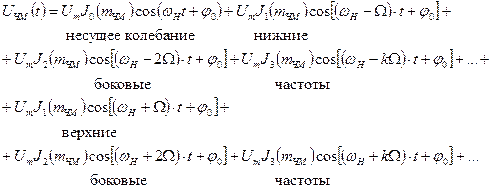(11)

Из (11) видно, сто спектр ЧМ сигнала при тональной модуляции содержит кроме несущей бесконечное число боковых составляющих, отстоящих на оси частот от значения w_Н на kW, где k – любое целое число от 1 … ¥.

Выражение (11) можно записать более компактно:

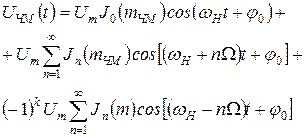(12)

Фазы боковых составляющих спектра ЧМ сигнала определяются для верхних боковых частот

j_п = j₀ + пf. (13)

Для четных гармоник нижних боковых частот

j_п = j₀ - пf. (14)

Для нечетных гармоник нижних боковых частот

j_п = j₀ – пf + p, (15)

где f – начальная фаза ПЭС.

Амплитуды боковых составляющих А_k пропорциональны соответствующим значениям функций Бесселя:

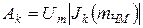(16)

На графиках рис. 2 по оси абсцисс отложены значения аргумента функций, по оси ординат - значение самих функций. В зависимости от номера гармоник выбирают соответствующую ей функцию Бесселя J_k (m). Значения функций Бесселя приводятся в справочниках по математике. Из графиков видно, что J_k (m) знакопеременные, убывающие функции. С ростом порядка k наибольшее значение функций уменьшается и отдаляется от начала координат.

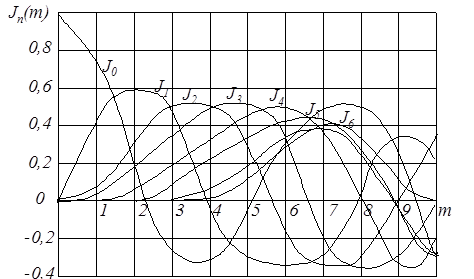
Рис. 2. Графики функции Бесселя

Поэтому у спектра ЧМ сигналов с увеличением индекса т_ЧМ происходит изменение структуры спектра (рис. 3). С увеличением т_ЧМ уменьшается амплитуда несущей и возрастают амплитуды боковых частот с большими номерами. Ширина спектра возрастает.

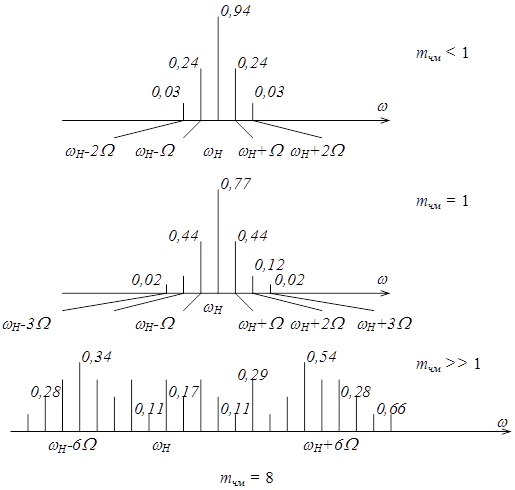
Рис. 3. Спектры ЧМ сигналов при тональной модуляции

При т_ЧМ << 1 спектр в своем составе имеет три составляющие, как и спектр АМ сигнала, но с противоположными боковыми. Расстояние по оси частот между любыми соседними спектральными составляющими равно частоте W модулирующего сигнала.

Для определения практической ширины спектра ЧМ сигнала обычно отбрасывают боковые составляющие, уровень которых намного меньше амплитуды немодулированной несущей. Если в спектре ЧМ сигнала пренебречь составляющими, уровень которых на 40 дБ (т.е. в 10000 раз меньше), то практическая ширина спектра равна

, (17)

а если пренебречь составляющими, уровень которых на 25 дБ меньше амплитуды немодулированной несущей, то

(18)

Выражения (17) и (18) называют формулами Манаева, которые позволяют определять ширину спектра ЧМ сигнала.

Date: 2015-07-24; view: 2315; Нарушение авторских прав