Энергетический спектр случайного процесса

При изучении различных преобразований случайных сигналов и помех желательно определить спектр, характеризующий не отдельную выборочную функцию, а весь ансамбль в целом. При попытке применить преобразование Фурье к случайным процессам возникают различные препятствия, преодоление которых заключается в отбрасывании некоторых параметров спектра, а именно спектра фаз, и построении функции, характеризующей распределение энергии процесса по оси частот.

Рассмотрим непериодический сигнал S (t), обладающий свойством абсолютной интегрируемости:

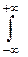½ S (t), ½d t <¥. (1)

Для такого сигнала могут быть определены прямое и обратное преобразование Фурье (интегралы Фурье):

G (j 2 p f)= 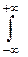S (t) e ^{- j 2 pf t} d t; (2)

S (t)= 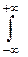G (j 2 p f) e ^{- j 2 pf t} d t. (3)

Функция частоты G (j 2 p f) называется комплексной спектральной плотностью (КСП) сигнала S (t). Произведение G (j 2 p f)d t имеет смысл коэффициентов ряда Фурье, следующих через бесконечно малые интервалы частот d f и описывающих сигнал S (t) с бесконечно большим периодом.

Комплексную спектральную плотность можно представить в показательной форме:

G (j 2 p f)= ½ G (j 2 p f) ½ e^{jj (t)}.

Модуль КСП ½ G (j 2 p f) ½ называется спектром амплитуд, а аргумент j (t) - спектром фаз сигнала S (t). В отличие от ряда Фурье для периодических сигналов, эти спектры являются сплошными.

Рассмотрим сигнал, отличный от нуля на конечном интервале времени

[- T /2; T /2] и равный нулю вне этого интервала (рис.1).

Повторяя этот сигнал через период времени, получим периодический сигнал.

Сигнал S (t) удовлетворяет условию (1), поэтому для него существует прямое преобразование Фурье (2). С другой стороны, сигнал S (t) может быть представлен рядом Фурье (4) на интервале времени [- T /2; T /2].

S (t)= 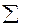S_ke^{j 2 pkf t}e ^{- j 2 pf t}. (4)

Подставляя (4) в (3) получим:

G (j 2 p f)= 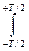S (t) e ^{- j 2 pf t} d t=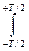 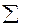S_ke^{j 2 pkf t}e ^{- j 2 pf t} d t=

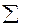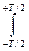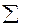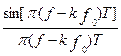= S_k e^{-j 2 p (f - kf) t} d t= S_kT . (5)

Выражение 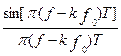= 0 при всех f = nf ₀¹ k f ₀,

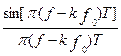= 1 при всех f = kf ₀, f ₀=1/T.

Поэтому, для f = k f ₀ КСП равна:

G (j 2 pk f ₀)= S_kT

или

½ G (j 2 pk f ₀) ½=½ S_k ½ T.

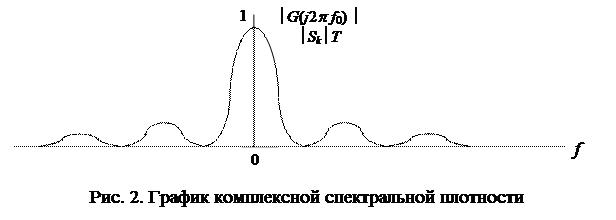
Таким образом, в точках f = kf _o модули коэффициентов ряда Фурье | S_k | с точностью до постоянного множителя T совпадают с огибающей спектра амплитуд сигнала S (t) (рис. 2).

Для реализации случайных сигналов и помех КСП является случайной функцией частоты.

Диапазон изменения амплитуд периодического сигнала определяется спектром Фурье одиночного сигнала.

Расстояние между дискретными частотами периодического сигнала - периодом повторения сигнала.

Это надо при построении генератора сетки стандартных частот. Коэффициенты комплексного ряда Фурье периодического сигнала, умноженные на T =const, представляют собой выборочные значения ("скелет") спектра Фурье одиночного сигнала.

Построение такой функции проведем сначала для процессов с конечной энергией, для которых существует случайная спектральная плотность S_x (j 2 p f). Каждая ее реализация соответствует реализации x (t), и для них, согласно теореме Парсеваля,

Ex= 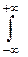½ x (t)½²d t = 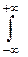½ S_x (j 2 p f)½²d t.

Функция ½ S_x (j 2 p f)½² характеризует, таким образом, распределение энергии реализации по оси частот. Назовем ее спектральной плотностью энергии реализации.

Усреднив эту функцию по всем реализациям, получим спектральную плотность энергии процесса

M {½ S_x (j 2 p f)½²}.

Отметим некоторые свойства спектральной плотности энергии. Из ее определения следует, что она неотрицательна. Кривая, изображающая эту функцию, охватывает площадь, равную математическому ожиданию энергии процесса. Она определена на бесконечной оси, т.е. как для положительных, так и отрицательных частот. Как известно из теории преобразований Фурье, для действительной функции x (t) модуль ½ S_x (j 2 p f)½ является четной функцией частоты. Поэтому о спектральном распределении энергии процесса можно судить и по одной половине графика.

Вывод. Таким образом энергетическим спектром стационарного случайного процесса называется распределение спектральной плотности мощности (дисперсии) по частоте.

Под спектральной плотностью мощности понимается мощность, приходящаяся на единицу полосы частот S (f)=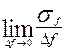

2. Связь между спектральными и временными характеристиками случайного процесса

Спектральную плотность мощности стационарного случайного процесса можно определить по его корреляционной функции на основании следующей теоремы Винера-Хинчина:

спектральная плотность мощности G (f) центрированного стационарного случайного процесса является преобразование Фурье от корреляционной функции B_X (t):

G_X (f)= 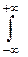B_X (t) e ^{- j 2 pft} d t.

Следствия из теоремы:

1. Из теории преобразования Фурье следует справедливость обратного преобразования

B_X (t)= 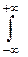G_X (f) e^{j 2 pft} d f.

2. Значение G (f) на нулевой частоте равно интегралу корреляционной функции.

3. Так как G (f) - неотрицательная функция, то корреляционными функциями случайных процессов могут быть только такие, которые имеют положительное преобразование Фурье. В частности, например, прямоугольная функция не может быть корреляционной.

Так как G (f) является четной функцией пару преобразований Винера-Хинчина можно записать в более компактном виде:

G (f)=2 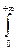B_X (t)cos(2 pft) d t,

B_X (t)=2 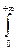G (f)cos(2 pft) d f= 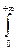G ₀(f)cos(2 pft) d f.