Размещения

Кортежи длины k (1≤k≤n), состоящие из различных элементов n- элементного множества A (кортежи отличаются один от другого как самими элементами, так и их порядком), называются размещениями из n элементов множества A по k. Число таких размещений обычно обозначается 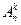(буква A от французского слова arrangement - размещение) или |n|^k.

Схема выбора состоит в выборе k элементов из n- элементного множества без возвращения. Для этого необходимо совершить k действий: первое действие можно совершить n способами, второе уже n -1 способами, а k -е действие n – (k – 1) способами. Согласно вышеуказанному правилу произведения получаем конечное число перестановок 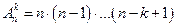. Умножим и разделим на 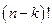, получим:

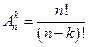
Отличие размещения от перестановки. Если размещения отличаются друг от друга только порядком, так как в каждом из них встречаются по одному разу все элементы множества A, то такие размещения являются перестановками, т.е. .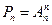

Пример. Дано A = {1, 2, 3}. Найти все размещения из трех элементов по два и их число.

Решение. <1, 2>; <1, 3>; <2, 3>; <2, 1>; <3, 1>; <3, 2>. Число размещений, как видно равно 6.

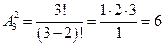
Подчеркнем еще раз, что приведенная формула справедлива, если множество A состоит из разных элементов.