Мультиквадриковый способ аппроксимации топографической поверхности

В этом способе аппроксимация топографической поверхности осуществляется путем суммирования поверхностей заранее фиксированного вида, в качестве которых применяются конусы и гиперболоиды. Каждая такая поверхность, характеризуемая уравнением

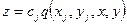
связана с некоторой точкой топографической поверхности j и имеет определенный наклон c_j. Элемент 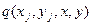называется кадрикой точки j.

Для n квадрик аппроксимирующая топографическую поверх­ность формула получается как сумма частных квадрик

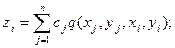
и называется мультиквадриковой поверхностью.

Квадрика q, представляемая гиперболоидом, имеет вид

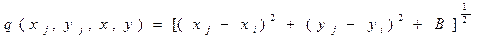(5.8)

При В=0 гиперболоид превращается в круговой конус, радиус основания которого равен высоте, а вершина лежит в плоскости XOY. Координаты вершины совпадают с координата­м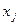и и 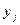точки j.

Коэффициенты 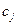получаются из решения системы n урав­нений

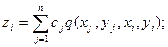i=1, 2, …, n (5.9)

где 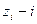-я компонента вектора z=[ 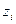] 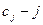-я компонента вектора неизвестных коэффициентов ; q(x_j, y_j, x_i, y_i)— эле­менты q_i матрицы

Q = [q_ij ],

В матричной форме система уравнений (1) примет вид

Qc=z

откуда

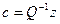
С геометрической точки зрения коэффициенты с_j — танген­сы углов наклона образующих соответствующих конусов к плоскости XOY.

Координата z_A любой определяемой точки на вычисленной мультиквадриковой поверхности получается как сумма всех z_j^A точек пересечения каждой частной квадрики с вертикаль­ной линией, проходящей через точку A,

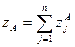
Величина параметра В в формуле (5.8) может принимать различные значения в зависимости от сложности рельефа и размеров стороны квадрата.

Как показали исследовании, мультиквадриковая поверхность наиболее адекватна топографической поверхности, когда значение параметра В имеет тот же порядок, что и квадрат стороны участка аппроксимации. При неправильном выборе этого параметра происходит систематический сдвиг поля высот.

Date: 2015-07-24; view: 538; Нарушение авторских прав