Законы Ома и Джоуля-Ленца с учетом поля сторонних сил

Опираясь на дифференциальную форму закона Ома, с учетом того, что в цепь включен источник ЭДС, получим:

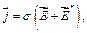где - напряженность электрического поля сторонних сил.

Рассмотрим ток, который формируется вдоль тонкого проводника:

Скалярно домножим на 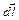и проинтегрируем от сечения 1 до сечения 2:

.

Учтем, что 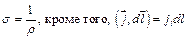, , тогда получим следующее выражение:

-

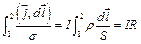
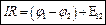интегральная форма закона Ома с учетом поля сторонних сил для участка цепи, содержащего ЭДС.

Рассмотрим произвольную цепь с произвольным числом узлов и обратим внимание на контур 1-2-3-1.

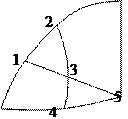Обозначим величину тока в отрезке ik

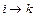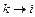Будем считать, что если ток течет от , то он положителен , и,наоборот, если , то ток отрицателен. .

,

Суммируя по всему контуру:

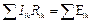- это утверждение называют обычно вторым законом Кирхгофа.

Вспомним также, что - первый закон Кирхгофа. Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю. Это утверждение вытекает из условия стационарности постоянного тока или закона сохранения заряда.

Считается, что система из этих уравнений полностью описывает любую цепь постоянного тока.

Вернемся к нашей записи:

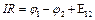- умножим на .

(*)

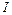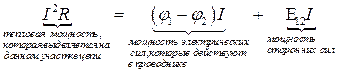Применив (*) ко всей неразветвленной цепи (тогда 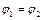), получим, что

дифференциальная форма или удельная мощность записывается как .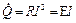

То есть общее количество выделяемой за единицу времени во всей цепи джоулевой теплоты равно мощности только сторонних сил. Значит, теплота производится только сторонними силами. Роль же электрического поля сводится к тому, что оно перераспределяет эту теплоту по различным участкам цепи.

Получим теперь это уравнение в локальной (дифференциальной) форме, умножим на 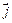и учтем, что и - дифференциальную форму закона Джоуля-Ленца.

Тогда удельная тепловая мощность тока в неоднородной проводящей среде записывается так:

.

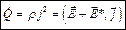Date: 2015-07-24; view: 349; Нарушение авторских прав