Вычти 3

Первая из них увеличивает число на экране на 6, вторая – уменьшает на 3. Если в ходе вычислений появляется отрицательное число, он выходит из строя и стирает написанное на экране.

Программа для Калькулятора – это последовательность команд. Сколько различных чисел можно получить из числа 1 с помощью программы, которая содержит ровно 10 команд?

Решение:

1) особенность этой задачи – у дополнении к условию: «Если в ходе вычислений появляется отрицательное число, он выходит из строя и стирает написанное на экране»

2) сначала решим задачу без этого ограничения; поскольку две команды 1 и 2 можно переставлять (последовательное применение команд 1 и 2 дает тот же результат, что и последовательное применение команд 2 и 1), количество различных чисел, которые можно получить с помощью программы из N = 10 команд равно N+1 = 11 (см. разборы задач, приведенные выше)

3) проблема в том, что из этих 11 чисел нужно выбросить все отрицательные, так как при появлении отрицательного числа исполнитель выходит из строя

4) минимальное число получается, если применить к начальному числу 10 команд 2:

1 – 10·3 = –29

5) соседние числа в дереве (см. выше) отличаются на 6 – (–3) = 9, поэтому эти 11 чисел

–29 –20 –11 –2 7 16 25 34 43 52 61

6) из них только 7 чисел положительные

7) Ответ: 7.

Решение (2 способ):

1) заметим, что поскольку две команды 1 и 2 можно переставлять (последовательное применение команд 1 и 2 дает тот же результат, что и последовательное применение команд 2 и 1), количество различных чисел, которые можно получить с помощью программы из N = 10 команд равно N+1 = 11 (см. разборы задач, приведенные выше)

2) разница между соседними числами равна (+6)-(-3)=9 (команды «+6» и «-3»)

3) начальное число – 1, наибольшее число можно получить, применив 10 команд увеличения на 6; получается число

1 + 10·6 = 61

4) строим ряд чисел – арифметическую прогрессию с разностью (–9):

61 52 43 34 25 16 7 …

все остальные значения отрицательные

5) таким образом, можно получить только 7 положительных чисел

6) это значение можно посчитать сразу, не выписывая все числа; ответим на вопрос «Сколько раз можно отнять 9 от числа 61, чтобы получить первое отрицательное число» – получим 7, так как 61 – 9·7 = –2

7) Ответ: 7.

Решение (3 способ, неравенство, А.А. Серокурова, лицей №6, г. Тольятти):

1) по условию программа содержит только операции сложения («+6») и вычитания («-3»), которые можно переставлять, не меняя результат

2) поэтому число, получаемое в результате выполнения некоторой программы из числа 1, можно представить в виде

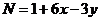
где 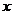– количество команд «+6», а 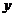– количество команд «-3»

3) поскольку по условию всего в программе 10 команд, получаем 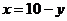, что дает

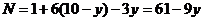
4) нам требуется определить, сколько неотрицательных чисел может быть получено таким образом, поэтому получаем неравенство

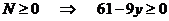
5) решая последнее неравенство, получаем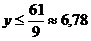

6) поскольку 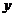– целое число, получаем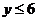

7) с другой стороны, количество команд «-3» не может быть меньше нуля, поэтому

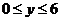
8) очевидно, что в этом диапазоне находятся 7 значений 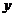(от 0 до 6 включительно), что позволяет получить 7 различных неотрицательных чисел

9) Ответ: 7.

Ещё пример задания:

У исполнителя Акробат три команды:

Вверх

Влево

Вправо

При выполнении этих команд Акробат перемещается на одну клетку, соответственно вверх, влево или вправо. Программа для Акробата – это последовательность команд. Он находится в центре поля. После выполнения программы исполнитель оказывается в какой-то клетке поля. Сколько таких клеток на поле, в которых может оказаться Акробат после выполнения различных программ, состоящих из четырех команд.

Решение (1 способ, уравнение, перебор):

1) Акробат перемещается по клетчатой доске, поэтому можно рассматривать его движение как изменение координат по осям X и Y

2) пусть 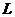– количество команд «влево», 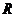– количество команд «вправо» и 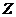- количество команд «вверх». Тогда изменения координат вычисляются как

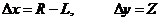
3) В программе 4 команды, поэтому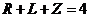

4) поскольку перемещение Акробата по оси Y определяется только значением 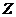, можно зафиксировать 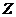(предположить, что оно равно какому-то числу) и при этих условиях найти, сколько есть таких клеток, в которые Акробат может попасть при этом 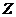; затем останется сложить все результаты для всех возможных значений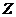

5) пусть 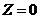, тогда 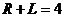и 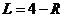; при этом получаем изменение координаты по оси Х:

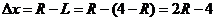
6) при условии, что 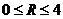возможно 5 разных допустимых целых значений 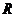, каждое из которых даёт своё значение 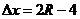; поэтому при 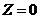есть 5 таких клеток

7) аналогично находим, что при 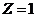существует 4 клетки, при 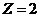есть 3 клетки и т.д.; увеличение 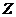на 1 приводит к уменьшению числа достижимых клеток на 1; при 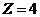остается одна единственная клетка;

8) складываем: 5 + 4 + 3 + 2 + 1 = 15.

9) Ответ: 15.

10) в общем виде: если программа для Акробата содержит 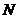команд, то число достижимых клеток равно (по формуле суммы членов арифметической прогрессии):

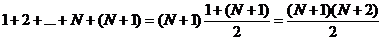
Задачи для тренировки [1]:

1) У исполнителя Калькулятор две команды:

Date: 2015-07-22; view: 372; Нарушение авторских прав