Приклад 3.2

Знайти точку умовного екстремуму функції 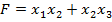при обмеженнях:

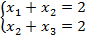
Розв’язання:

Складемо функцію Лагранжа 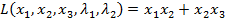+ 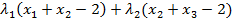і продиференціюємо її по змінних 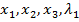і 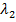. Прирівнюючи отримані вирази до нуля, отримаємо наступну систему рівнянь:

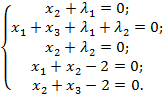
З першого і третього рівнянь випливає, що 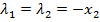, тоді

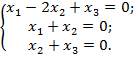
Розв’язуючи дану систему, знаходимо: .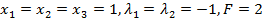

Побудуємо матрицю Гессе, що складається з елементів .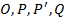

.

.

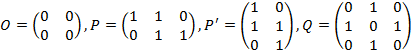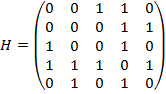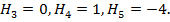
Отже 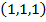— точка, у якій функція досягає максимального значення .

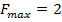4. Опуклі й угнуті функції

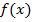Нехай задано -вимірний лінійний простір . Функція що задана на опуклій множині 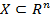, називається опуклою, якщо для будь-яких двох точок 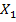та 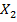з множини і будь-яких значень 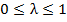, виконується співвідношення:

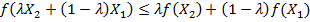(4.1)

Якщо нерівність строга і виконується для 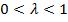, то функція 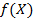називається строго опуклою.

Функція 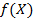, яка задана на опуклій множині ,
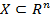називається угнутою, якщо для будь-яких двох точок 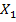та 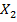з множини 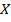і будь-якого 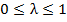справджується співвідношення:

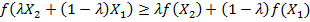(4.2)

Якщо нерівність строга і виконується для 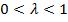, то функція 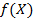називається строго угнутою.

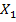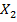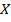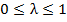Слід зазначити, що опуклість та угнутість функції визначаються лише відносно опуклих множин у , оскільки за наведеними означеннями разом з двома будь-якими точками та множині належать також точки їх лінійної комбінації: для всіх значень , що можливо лише у разі, коли множина 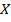є опуклою.

Теорема 4.1.

Нехай 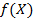— опукла функція, що задана на замкненій опуклій множині 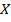, тоді будь-який локальний мінімум 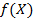на цій множині є і глобальним.

Теорема 4.2.

Нехай 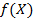— опукла функція, що визначена на опуклій множині 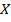, і крім того, вона неперервна разом з частинними похідними першого порядку в усіх внутрішніх точках 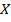. Нехай 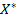— точка, в якій 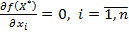. Тоді в точці 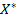досягається локальний мінімум, що збігається з глобальним.

5. Теорема Куна-Таккера

Розглянутий метод множників Лагранжа уможливлює знаходження лише локальних сідлових точок функції Лагранжа.

Теорема Куна-Таккера дає змогу встановити типи задач, для яких на множині допустимих розв’язків існує лише один глобальний екстремум зумовленого типу. Вона тісно пов’язана з необхідними та достатніми умовами існування сідлової точки.

Розглянемо задачу нелінійного програмування, яку, не зменшуючи загальності, подамо у вигляді:

(5.1)

за умов:

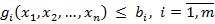(5.2)

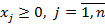(5.3)

Теорема 5.1. (Теорема Куна-Таккера).

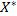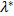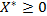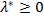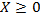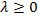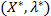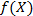Вектор є оптимальним розв’зком задачі (5.1)-(5.3) тоді і тільки тоді, коли існує такий вектор , що при , для всіх , точка є сідловою точкою функції Лагранжа , і функція мети для всіх 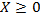угнута, а функції 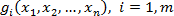— опуклі.

6. Опукле програмування

Опукле програмування розглядає методи розв’язування задач нелінійного програмування, математичні моделі яких містять опуклі або угнуті функції.

Загальний вигляд задачі опуклого програмування такий:

(6.1)

за умов:

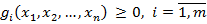(6.2)

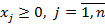(6.3)

де 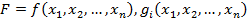— угнуті функції.

Аналогічний вигляд має задача для опуклих функцій.

Позначимо: 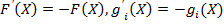, тоді 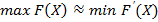, і маємо:

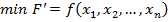(6.4)

за умов:

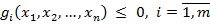(6.5)

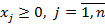(6.6)

де 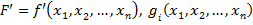— опуклі функції.

Оскільки ці задачі еквівалентні, то нижче розглянемо задачу (6.1)—(6.3).

Множина допустимих планів задачі, що визначається системою (6.2), є опуклою.

Як наслідок теорем 4.1 та 4.2 справджується таке твердження: точка локального максимуму (мінімуму) задачі опуклого програмування (6.1)—(6.3) є одночасно її глобальним максимумом (мінімумом).

Отже, якщо визначено точку локального екстремуму задачі опуклого програмування, то це означає, що знайдено точку глобального максимуму (мінімуму).

У разі обмежень-нерівностей задачу опуклого програмування розв’язують, застосовуючи метод множників Лагранжа.

Функція Лагранжа для задачі (6.1)—(6.3) має вид:

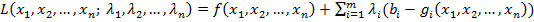(6.7)

де 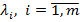— множники Лагранжа.

Використовуючи теорему Куна-Таккера, маємо необхідні та достатні умови існування оптимального плану задачі опуклого програмування.

Теорема 6.1.

Якщо задано задачу нелінійного програмування виду (6.1)—(6.3), де функції 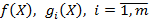диференційовні і вгнуті по 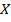, то для того, щоб вектор 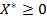, був розв’язком цієї задачі, необхідно і достатньо, щоб існував такий вектор 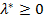, що пара 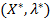була б сідловою точкою функції Лагранжа, тобто щоб виконувалися умови:

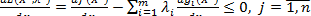(6.8)

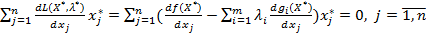(6.9)

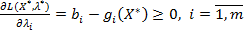(6.10)

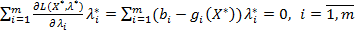(6.11)

Умови (6.9) і (6.11) називаються умовами доповнюючої нежорсткості. Умови (6.9) відносяться до всіх змінних, на які накладені умови невід’ємності, а (6.11) — до всіх обмежень-нерівностей виду (6.2).

Користуючись теоремою Куна-Таккера, задачу опуклого програмування розв’язують за наступним алгоритмом:

1. Складають функцію Лагранжа для задачі (6.1) - (6.3):

.

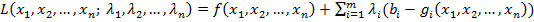2. Записують умови оптимальності (6.8)—(6.11).

3. Знаходять розв’язок 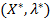системи рівнянь (6.9) і (6.11) та нерівностей (6.8) і (6.10). Зазначимо, що в даному випадку вектор 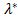повинен задовольняти умові невід’ємності.

Для розв’язування деяких класів задач нелінійного програму­вання застосовуються методи, які передбачають певний вид цільо­вої функції.

Так, для задач з опуклими цільовими функціями у вигляді квадратичної форми

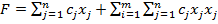, (6.12)

використовуються методи квадратичного програмування, які ґрунтуються на теоремі Куна-Таккера про існування екстремуму функції Лагранжа для досліджуваної задачі.

Якщо цільова функція задачі є сепарабельною, тобто її можна подати у вигляді алгебраїчної суми однорідних функцій відносно однієї змінної:

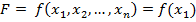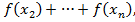+ (6.13)

тоді наближені екстремуми функцій визначаються методами лінійно-кускової апроксимації, їх основна ідея полягає в кусково-лінійній апроксимації початкової нелінійної функції лінійними залежностями, які розглядаються для кожної складової сепарабельної функції в інтервалах, що визначені точками сітки. Досліджуючи зміни цих функцій на кінцях інтервалів, можна перетворити початкову нелі­нійну задачу на задачу лінійного програмування, яка оперує з приростами цільової функцій та обмежень.

7. Розв’язування задачі нелінійного програмування за допомогою пакету Mathcad

За допомогою системи комп’ютерної алгебри Mathcad знайдемо максимальне і мінімальне значення функцій із заданими умовами.

Розглянемо порядок дій для вирішення задачі нелінійного програмування у програмі Mathcad:

1. Розмістимо курсор (червоний хрестик) на місці, де ми хочемо ввести цільову функцію. Вводимо ім’я критерію оптимізації і в дужках його аргументи через кому. Вводимо знак присвоювання “:=”, після якого вводимо вираз. Ініціалізуємо змінні і надаємо їм початкові наближення.

2. Вводимо ключове слово Given. Після цього вводимо обмеження, використовуючи знаки з меню Boolean.

3. За допомогою меню Vector & Matrix створюємо вектор змінних. Вводимо знак присвоювання після якого вводимо функцію minimize або maximize і в дужках параметри 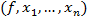. Нижче створюємо, ще один вектор змінних, після якого вводимо знак рівності. Отримаємо точку, в якій функція набуває критичного значення. Також можемо знайти значення функції в цій точці.

Демонстрація алгоритму на прикладах 3.1 і 3.2. та ін.:

1. 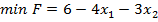, за умови: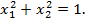

Рис. 7.1

2. 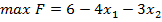, за умови: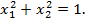

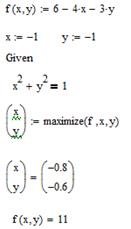
Рис. 7.2

3. 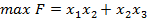, за умов: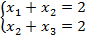

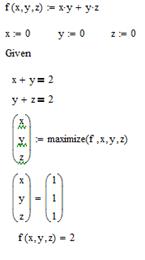
Рис. 7.3

4. 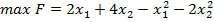, за умов: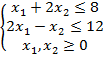

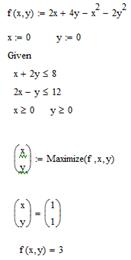
Рис. 7.4

5. 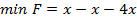, за умови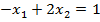

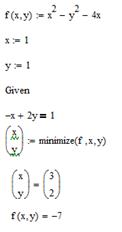
Рис. 7.5

6. 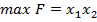, за умов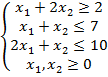

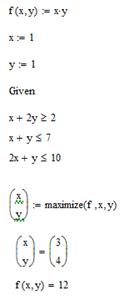
Рис. 7.6

7. 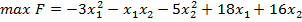, за умов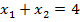

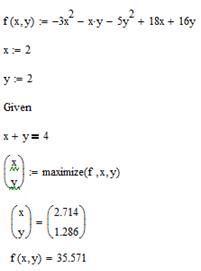
Рис 7.7

З рис. 7.1 бачимо, що дана програма рахує наближено і результат залежить від значень, які ви надасте змінним при ініціалізації. Початкові наближення потрібно вибирати так, щоб вони задовольнялись обмеженням, які накладаються на цільову функцію.

Висновок

В даній курсовій роботі ми розглянули розв’язування задач нелінійного програмування і застосували до їх розв’язання математичний пакет Mathcad. В теоретичній частина було розглянуто знаходження екстремальних значень методом множників Лагранжа. На практиці був описаний алгоритм для знаходження розв’язку оптимізаційної задачі на ЕОМ, а саме на базі математичного пакету Mathcad. Як бачимо, розглянуті методи не завжди дають точний результат, але його можна завжди легко покращити задавши інші початкові дані.

Переваги таких методів в тому, що алгоритм розв’язку можна легко запрограмувати, а відповідна програма буде потребувати мало ресурсів і часу виконання на ЕОМ.

Список використаної літератури

Date: 2015-07-24; view: 571; Нарушение авторских прав